Find Maximum Subarray Sum using divide and conquer

Reading time: 20 minutes | Coding time: 10 minutes

We are interested in to find maximum subarray sum (contiguous) of given 1-D array. Array may contain negative and positive numbers which makes this a difficult problem. Brute force will take O(N^2) time while a divide and conquer approach will take O(N log N) time.

• If all the array entries were positive, then the maximum-subarray problem would present no challenge, since the entire array would give the greatest sum.
• Example : input array = [-3,2,3,4,-4,-1].
  • here maximum subarray is [2,3,4]. hence maximum subarray sum is 9.

Two approaches:

• Simple approach is brute-force implementation but it will take O(n^2) time.
• Divide and conquer algorithm will give maximum subarray in O(nlogn) time.

Brute-force Implementation O(N^2)

The idea is to generate all subarrays, compute sum of each subarray and keep the subarray having the largest sum. This approach takes O(N^2) time complexity.

import java.util.*;
public class recursion 
{
	public static void main(String[] args) 
    {
		int arr[]= {-2,-4,8,4,3,3,-9};
        System.out.println("Maximum Subarray Sum is "+maximumsubarray(arr,arr.length));
	}
	public static int maximumsubarray(int arr[],int high)
    { 
	   int maxsum=Integer.MIN_VALUE;
       for(int i=0; i < high; i++)
       {
    	   int sum=0;
    	   for(int j=i; j < high; j++)
    	   {
    		   sum+=arr[j];
    		   if(sum>=maxsum)
    			   maxsum=sum;
    	   }
       }
       return maxsum;
  }      
}

• The outer loop will take the starting element, the inner loop finds the maximum possible sum with first element picked by outer loop and compares this maximum with the overall maximum. Finally return the overall maximum.

• So Basically we are checking all possible subarray for given element and each time we compare it with overall maximum.

• Brute-force algorithm will take O(n^2) time.

Divide and Conquer algorithm O(N log N)

1. Divide an array in two halves.
2. Find maximum subarray sum in left half.
3. Find maximum subarray sum in right half.
4. Find maximum subarray sum which crosses the midpoint.
5. Maximum of step 2,3 and 4 is our answer.

• Divide and Conquer technique suggest that divide the subarray into two subarrays of as equal size as possible. for that we find mid point of an array.
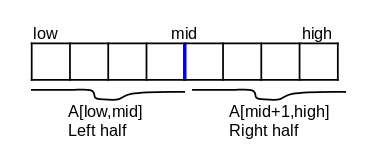
• consider subarray A[low,mid] and A[mid+1,high] as shown in figure 1.
• any contigues maximum subarray lie between three following places :

1. entirely in the leftside subarray (A[low,mid])
2. entirely in the rightside subarray(A[mid+1,high]).
3. crossing the midpoint (A[i,j]).(figure 2)

• figure 1
• 
• figure 2
• 
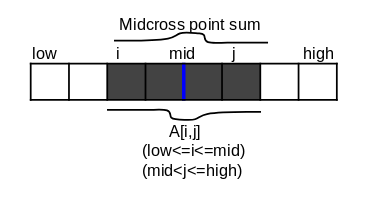
• find the location of maximum subarray in this three places.
• Divide and Conquer technique will return maximum subarray of the left and right subarray.
• But We need maximum subarray of an given array. so we need to check an subarray which crosses the midpoint. this subarray contain elements from both left and right.
• to find this subarray we could simply start from midpoint then traverse toward the left side of an midpoint till sum is increasing. do the same process on left side of an midpoint.(start from mid+1 index) .
• Example : input array {-3,2,5,6,7,1,-3,-2}
  • Divide and Conquer technique will return 13 (A[1,3]) for left subarray. and 8 (A[4,5]) for right subarray.
  • if we find subarray (A[1,5]) which cross the midpoint then answer should be 21.

Example :

• Input array =[-6,-2,8,3,4,-2].
• here maximum contiguous subarray sum from left-side is 8 .
• maximum contiguous subarray sum from right-side is 7.
• midpoint cross subarray sum is 15.
• hence the maximum subarray sum is 15.
  

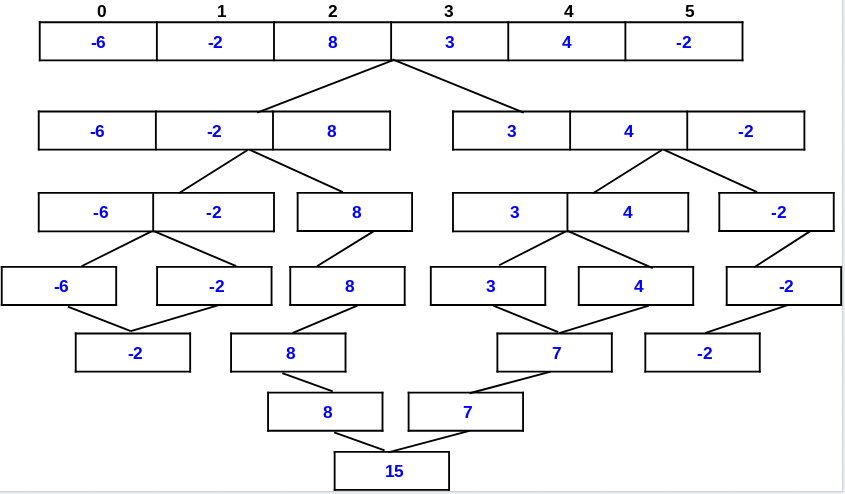
Pseudo code :

Left_Right_MaximumSubarray(A,low,high)
if high==low      // base case
  return A[low]
else 
mid=(low + high)/2 
leftsum=Left_Right_MaximumSubarray(A,low,mid)
rigthsum=Left_Right_MaximumSubarray(A,mid+1,high)
midcrosssum=Midpoint_Crosssum(A,low,mid,high)
return maximum(leftsum,rightsum,midcrosssum)
endfunction

Midpoint_Crosssum(A,low,mid,high)
sum=0
leftsum=-∞
for i=mid downto low
   sum=sum+A[i]
   if sum>leftsum
      leftsum=sum
sum=0
rightsum=-∞ 
for i=mid+1 to high
   sum=sum+A[i]
   if sum>rightsum
      rightsum=sum
return leftsum+rightsum      
endfunction

Implementation :

import java.util.*;
public class Maximumsubarray {
	public static int Midpoint_Crosssum(int arr[], int low, int mid, int high) 
    { 
		int sum = 0; 
		int leftsum = Integer.MIN_VALUE; 
		for (int i = mid; i &gt= low; i--) 
		{ 
			sum = sum + arr[i]; 
			if (sum &gt leftsum) 
			   leftsum = sum; 
		} 
		sum = 0; 
		int rightsum = Integer.MIN_VALUE; 
		for (int i = mid + 1; i &lt= high; i++) 
		{ 
		  sum = sum + arr[i]; 
		  if (sum &gt rightsum) 
		    rightsum = sum; 
		} 
	 return leftsum + rightsum; 
    } 
  public static int Left_Right_MaximumSubarray(int arr[], int low, int high) 
       {  
			if (low == high) 
			    return arr[low];  
			else 
			{int mid = (low + high)/2; 
			return Math.max(Math.max(Left_Right_MaximumSubarray(arr, low, mid), Left_Right_MaximumSubarray(arr, mid+1, high)), Midpoint_Crosssum(arr, low, mid, high)); 
			}
		} 
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int arr[] = {2, 4, -6, -2, 3,8};  
	    int maxsum = Left_Right_MaximumSubarray(arr, 0, arr.length-1); 	      
	    System.out.println("Maximum subarray sum is "+ maxsum); 
	}

}

Output :

Maximum subarray sum is 11

Time Complexity :

• T(n)=Θ(1) if n=1
• T(n)=2T(n/2)+Θ(n) if n>1.
• This recurrence can be solved using master's theorem and we will get T(n)=Θ(nlogn)