Minimum number of increment or decrement (by 1) operations to make array in increasing order

Given an array of size N. Find the minimum number of increment or decrement operations to make the array in increasing order. In each move, we can add or subtract 1 to any element in the array.

This problem can be solved in O(N x R) time where N is the number of elements and R is the range of the elements. This is achieved using Dynamic Programming.

Examples:

Input : a = { 5, 6, 6, 3 }
Output : 3
Explanation : Modified array is { 5, 6, 6, 6 }

Input : a = { 1, 2, 2, 3 }
Output : 0
Explanation : Given array is already in increasing order
    
Input : a = { 2, 3, 2, 5, 4 }
Output : 2
Explanation : Modified array is { 2, 3, 3, 5, 5 } or { 2, 2, 2, 4, 4} 

Go through this problem where we find the minimum number of increment (by 1) operations to make array in increasing order (no decrement operation). This variant is much simpler.

Intuition

Since we want to minimize the number of operations needed to make the array in increasing order, we can follow:

• A number will never be decreased to a value less than the minimum of the initial input array.
• A number will never be increased to a value greater than the maximum of the initial input array.
• The number of operations required to change a number from 'x' to 'y' is abs(x – y).

Based on the above intuitions, this problem can be solved using dynamic programming.

Algorithm

• Let DP(i, j) represent the minimum operations needed to make the 1st 'i' elements of the array sorted in increasing order when the ith element is equal to j.

DP(I, J) = Minimum number of operations to make the first I-th elements
           sorted in increasing order where I-th element = J

• Now DP(N, j) needs to be calculated for all possible values of j where N is the size of the array. According to the intuitions, j ≥ smallest element of the initial array and j ≤ the largest element of the initial array.

• The base cases in the DP(i, j) where i = 1, is the minimum number of operations needed to sort the 1st element in increasing order such that the 1st element is equal to j. So, DP(1, j) = abs( array[1] – j).

DP(1, j) = abs( array[1] – j)

• Now we would consider DP(i, j) for i > 1. If ith element is set to j, then the 1st (i – 1) elements need to be sorted and the (i – 1)th element has to be ≤ j i.e. DP(i, j) = (minimum of DP(i – 1, k) where k goes from 1 to j) + abs(array[i] – j)

DP(i, j) = (minimum of DP(i – 1, k) where k goes from 1 to j) + abs(array[i] – j)

Using the above recurrence relation and the base cases, the result can be calculated.

Algorithm ( array a[] , size of array or n )
{
    s = smallest element of array
    l = largest element of array
    dp[n][l+1]                 // initialise dp array.
    for j = s till l:          // filling the base case of dp array with absolute difference between first element and j 
        dp[0][j] = abs(a[0] - j) 
    for i = 1 till n :         // Iterate to fill the dp array.
    {
        minimum = INT_MAX      // Setting the local minimum to a MAX value
        for j = s till l :
        {
            Compare between 'minimum' variable and upper row (same column) element.
            Set minimum = min( previous minimum value, upper row (same column) element) 
            Set dp[i][j] = 'minimum' variable + absolute diffrence a[i] & j i.e. abs(a[i] - j)
        }
    }
    for j = s till l :
        set ans as the min value in the last row of dp array i.e. min value in dp[n-1][j]
    print the value of ans
}

Execution :

Starting from the below array input.

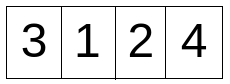
's' is initialized with 1 and 'l' is initialized with 4.
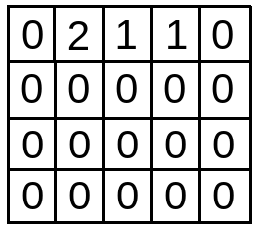
dp array is formed of size (n,l+1) i.e. dp[4][5].
The base case of dp is dp[0][j] is formed as below. (dp[0][j] for j = s to l).

Iteration starts from 2nd index onwards i.e. i = 1 till i < n or i < 4. In each iteration, subsequent rows of dp array are filled.

In the 1st iteration (i = 1), minimum is first set to INT_MAX.

Then for j = s till l (here 1 till 4), dp[i][j] is updated.

• when j = s i.e. 1 , minimum = dp[0][1] = 2 . So, dp[i][j] i.e. dp[1][1] = minimum + abs(a[i]-j) = 2 + abs(1-1) = 2.
• when j = 2 , minimum = min(minimum,dp[0][2]) i.e.min(2,1) = 1 . So, dp[i][j] i.e. dp[1][2] = minimum + abs(a[i]-j) = 1 + abs(1-2) = 2
• when j = 3 , minimum = min(minimum,dp[0][3]) i.e.min(1,1) = 1 . So, dp[i][j] i.e. dp[1][3] = minimum + abs(a[i]-j) = 1 + abs(1-3) = 3
• when j = 4 , minimum = min(minimum,dp[0][4]) i.e.min(1,0) = 0 . So, dp[i][j] i.e. dp[1][4] = minimum + abs(a[i]-j) = 0 + abs(1-4) = 3
• With j=5, inner iteration ends.

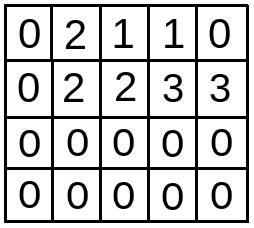
In the 2nd iteration (i = 2), minimum is first set to INT_MAX.

Then for j = s till l (here 1 till 4), dp[i][j] is updated.

• when j = s i.e. 1 , minimum = dp[1][1] = 2 . So, dp[i][j] i.e. dp[2][1] = minimum + abs(a[i]-j) = 2 + abs(2-1) = 3.
• when j = 2 , minimum = min(minimum,dp[1][2]) i.e.min(2,2) = 2 . So, dp[i][j] i.e. dp[2][2] = minimum + abs(a[i]-j) = 2 + abs(2-2) = 2
• when j = 3 , minimum = min(minimum,dp[1][3]) i.e.min(2,3) = 2 . So, dp[i][j] i.e. dp[2][3] = minimum + abs(a[i]-j) = 2 + abs(2-3) = 3
• when j = 4 , minimum = min(minimum,dp[1][4]) i.e.min(2,3) = 2 . So, dp[i][j] i.e. dp[2][4] = minimum + abs(a[i]-j) = 2 + abs(2-4) = 4
• With j=5, inner iteration ends.

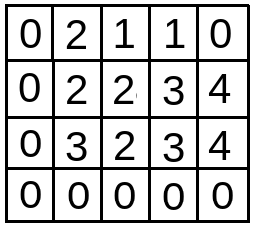
In the 3rd iteration (i = 3), minimum is first set to INT_MAX.

Then for j = s till l (here 1 till 4), dp[i][j] is updated.

• when j = s i.e. 1 , minimum = dp[2][1] = 3 . So, dp[i][j] i.e. dp[3][1] = minimum + abs(a[i]-j) = 3 + abs(4-1) = 6.
• when j = 2 , minimum = min(minimum,dp[2][2]) i.e.min(3,2) = 2 . So, dp[i][j] i.e. dp[3][2] = minimum + abs(a[i]-j) = 2 + abs(4-2) = 4
• when j = 3 , minimum = min(minimum,dp[2][3]) i.e.min(2,3) = 2 . So, dp[i][j] i.e. dp[3][3] = minimum + abs(a[i]-j) = 2 + abs(4-3) = 3
• when j = 4 , minimum = min(minimum,dp[2][4]) i.e.min(2,4) = 2 . So, dp[i][j] i.e. dp[3][4] = minimum + abs(a[i]-j) = 2 + abs(4-4) = 2
• With j=5, inner iteration ends.
• With i=5, outer iteration also ends.

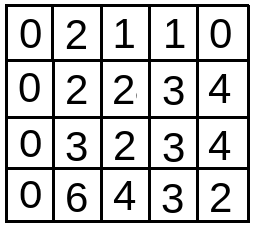
For finding the minimum value in last row i.e. 3rd row, we have to run a for loop in dp[n-1] row with j from s till l ( 1 till 4 )after initialising ans with INT_MAX:

• With j = s = 1, ans = min(ans,dp[n-1][j]) = min (INT_MAX,dp[3][1]) = min(INT_MAX,6) = 6.
• With j=2, ans = min(ans,dp[n-1][j]) = min (6,dp[3][2]) = min(6,4) = 4.
• With j=3, ans = min(ans,dp[n-1][j]) = min (4,dp[3][3]) = min(4,3) = 3.
• With j=4, ans = min(ans,dp[n-1][j]) = min (3,dp[3][4]) = min(3,2) = 2.
  As, j reaches 5, the iteration ends with ans being 2.

So, the output is 2.
The output array can be thought of as { 2, 2, 2, 4 }

Implementation Code :

#include <bits/stdc++.h> 
using namespace std; 

// function to find minimum number of increment or decrement (by 1) operations to make the array in increasing order. 

int Get_Minimum_Opr(vector<int> &a, int n) 
{ 

    // Finding the smallest element in the array 
    int s = *min_element(a.begin(), a.end()); 
  
    // Finding the largest element in the array 
    int l = *max_element(a.begin(), a.end()); 
  
    /* 
    dp(i, j) represents the minimum number of operations needed to make the array[0 .. i] sorted in increasing order with ith element is j. 
    */
    
    int dp[n][l + 1]; 
  
    // Filling the dp[][] array for base cases 
    for (int j = s; j <= l; j++) { 
        dp[0][j] = abs(a[0] - j); 
    } 
  
    /* 
    Using results for the first (i - 1) elements, calculate the result for the ith element. 
    */
    
    for (int i = 1; i < n; i++) { 
        int minimum = INT_MAX; 
        for (int j = s; j <= l; j++) { 
        
        /* 
            If the ith element is j then we can have any value from s to j for the (i-1)th element 
            We choose the one that requires the minimum number of operations. 
        */
        
            minimum = min(minimum, dp[i - 1][j]); 
            dp[i][j] = minimum + abs(a[i] - j); 
        } 
    } 
  
    /* 
        If we made the (n - 1)th element equal to j we would require dp(n-1, j) operations.
        We choose the minimum among all possible dp(n-1, j) where j goes from small to large 
    */
    
    int ans = INT_MAX; 
    for (int j = s; j <= l; j++) { 
        ans = min(ans, dp[n - 1][j]); 
    } 
    
    // return required answer 
    return ans; 
} 

// Driver code 
int main() 
{ 
    vector<int> arr ;
  	int n,a;
    cout<<"Enter the total number of elements in the array"<<endl;
  	cin>>n;
    for(int i=0;i<n;i++)
    {
            cout<<"Enter the element"<<endl;
            cin>>a;
            arr.push_back(a);
    } 
    cout << Get_Minimum_Opr(arr,n); 
    return 0; 
} 

Input :

{ 3, 2, 1, 4 }

Output :

2

Time & Space Complexity

Time complexity for the above approach is O(N * R) where N is the number of elements in the array and R = (largest element of the array – smallest element of the array + 1).

Space complexity for the above approach is O(N * (L+1)) where L is the largest element in the array, for the Get_Minimum_Opr function which makes the dp array.

With this article at OpenGenus, you must have the complete idea of the algorithm to find the minimum number of increment or decrement (by 1) operations to make array in increasing order. Enjoy.

Go through this problem where we find the minimum number of increment (by 1) operations to make array in increasing order (no decrement operation). This variant is much simpler.