
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Given an array of size N . Find the number of increment (by 1) operations required to make the array in increasing order. In each move, we can add 1 to any element in the array.
This can be solved in linear time O(N) using a Mathematical Algorithm.
Examples:
Input : a = { 5, 6, 6, 3 }
Output : 6
Explanation : Modified array is { 5, 6, 7, 8 }
Input : a = { 1, 2, 3 }
Output : 0
Input : a = { 1, 4, 3 }
Output : 2
Explanation : Modified array is { 1, 4, 5 }
Intuition
Let’s take two numbers p and q.
If p >= q, it can be converted into p < q by adding 1 as per the requirement of the question.
So, p < (q + k*1) for some value k
=> ( p – q ) < k
Thus, the minimum possible value of k is ( p – q ) + 1.
Algorithm
count = 0 // to act as a counter
for i = 1 till n-1 : // Iterate over the input array.
{
Take the two elements when a[i] >= a[i-1]
{
calculate their difference
add the above value + 1 both to the count and the a[i]
}
}
print the value of count
Execution
- Starting from the below array input. count is initialized with 0 and iteration starts from 2nd index onwards i.e. i = 1 till i < n or i < 4
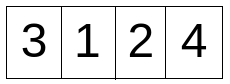
- In the 1st iteration (i = 1), a[i] i.e. a[1] = 1, which is less than a[i-1] i.e. a[0] = 3. Hence, p = ( a[i-1] - a[i]) +1 ) = 3 - 1 + 1 = 3
Previously count was initialized with the value 0. Now it is increased by 3 after this iteration to 3 i.e. count = 3 now.
a[i] is increased by 3 to 4 from 1.
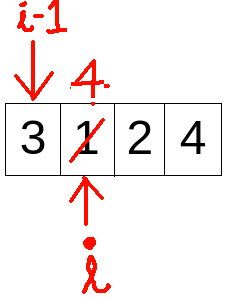
- In the 2nd iteration (i = 2), a[i] i.e. a[2] = 2, which is less than a[i-1] i.e. a[1] = 4. Hence, p = ( a[i-1] - a[i]) +1 ) = 4 - 2 + 1 = 3
Previously count had the value 3. Now it is increased by 3 after this iteration to 6 i.e. count = 6 now.
a[i] is increased by 3 to 5 from 2.
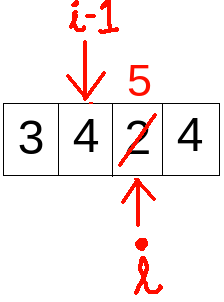
- In the 3rd iteration (i = 3), a[i] i.e. a[3] = 4, which is less than a[i-1] i.e. a[2] = 5. Hence, p = ( a[i-1] - a[i]) +1 ) = 5 - 4 + 1 = 2
Previously count had the value 6. Now it is increased by 2 after this iteration to 8 i.e. count = 8 now.
a[i] is increased by 2 to 6 from 4.
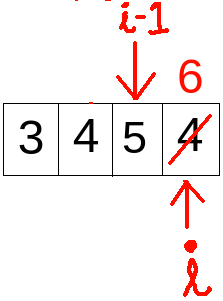
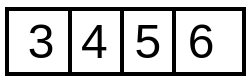
- Since i becomes 4 in the following iteration, which is not smaller than n=4 here, thus the loop stops and we get the final array as below with count=8, hence the output.
Implementation Code
#include <bits/stdc++.h>
using namespace std;
// function to find minimum number of increment (by 1) operations to make the array in increasing order.
int Minimum_Moves(vector<int> &a, int n)
{
// to store answer
int count = 0;
// iterate over the vector container array
for (int i = 1; i < n; i++)
{
// if in non- increasing order
if (a[i] <= a[i - 1])
{
int p = (a[i - 1] - a[i]) + 1 ;
// add moves to answer
count += p;
// increase the element by 1
a[i] += p ;
}
}
// return required answer
return count;
}
// Driver code
int main()
{
vector<int> arr ;
int n,a;
cout<<"Enter the total number of elements in the array"<<endl;
cin>>n;
for(int i=0;i<n;i++)
{
cout<<"Enter the element"<<endl;
cin>>a;
arr.push_back(a);
}
cout << Minimum_Moves(arr, n);
return 0;
}
Input :
{ 3, 2, 1, 4 }
Output :
8
Time & Space Complexity
Time complexity for the above approach is O(N) where N is the number of elements in the array
Space complexity for the above approach is O(1) for the Minimum_Moves function as only a single int type variable is used to count the number of moves required.
With this article at OpenGenus, you must have the complete idea of the algorithm to find Minimum number of increment (by 1) operations to make array in increasing order. Enjoy.
