Multithreaded Quick Sort in C++

C++ is a powerful programming language that offers native support for multithreading. With C++, developers can create and control multiple threads of execution in their applications using the standard library's threading facilities. Leveraging C++'s multithreading capabilities, developers can design high-performance and scalable applications that fully utilize the processing power of modern multi-core CPUs. However, working with multithreading in C++ also requires careful handling of thread synchronization and communication to avoid potential issues, such as race conditions, deadlocks, and resource starvation.

Table of contents

1. Introduction
2. Multithreading and Parallelism
3. Implementing Multithreaded Quick Sort in C++
4. Complexity Analysis
5. Applications of Multithreaded Quick Sort
6. Questions and Exercises
7. Conclusion and Discussion

Introduction

This article provides an overview of the quicksort algorithm and its complexity. Quicksort is a sorting algorithm that uses a divide and conquer strategy to sort a list or array of elements by selecting a pivot element and dividing the array into two sub-arrays. One sub-array has elements smaller than the pivot, and the other sub-array has elements larger than the pivot. This process is repeated recursively until the entire array is sorted.

Quicksort has an average time complexity of O(n log n), making it one of the most efficient sorting algorithms available. However, its worst-case time complexity is O(n^2), which occurs when the pivot is poorly chosen, and the sub-arrays are unevenly split. This information is relevant to the article's topic, which focuses on implementing a multithreaded version of quicksort in C++.

The article explains that multithreading is a technique that enables multiple threads to execute concurrently and can significantly improve the performance of the quicksort algorithm by parallelizing the sorting process. The primary goal of this article is to provide a step-by-step guide to implementing multithreaded quicksort in C++ while analyzing its complexity and real-world applications.

Multithreading and Parallelism

This article will delve into the concept of multithreading and parallelism, exploring how these techniques can bolster the performance of quicksort.

Multithreading enables the simultaneous execution of multiple threads, which can lead to faster program execution. When applied to quicksort, multithreading can be utilized to parallelize the sorting process by dividing the list into smaller sub-lists, each of which can be sorted by a separate thread. This strategy is particularly effective for larger lists, resulting in significant reductions in overall execution time.

Parallelism is another approach that can improve the efficiency and speed of quicksort. It involves breaking down a problem into smaller sub-problems that can be solved concurrently by separate processors or threads. For quicksort, parallelism can be achieved by dividing the list into smaller sub-lists, each of which can be sorted in parallel by different processors or threads. This leads to faster execution times and increased efficiency.

The article will expound on the advantages of multithreading and parallelism for quicksort, including improved performance, faster execution times, and increased efficiency. It will also provide a detailed explanation of how to implement multithreaded quicksort in C++ and examine the algorithm's time and space complexity.

Implementing Multithreaded Quick Sort in C++

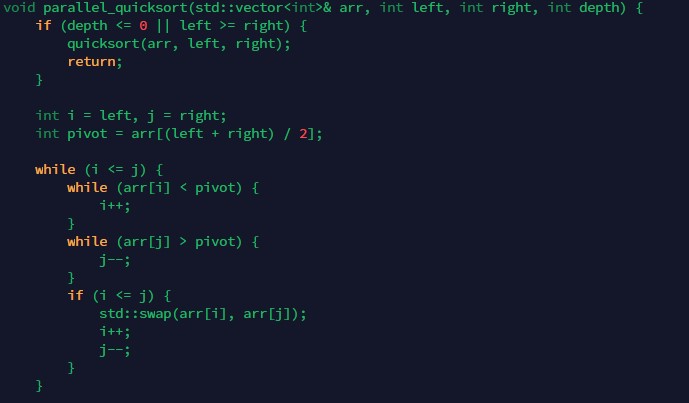
The section on implementing the Multithreaded Quick Sort in C++ aims to provide readers with a step-by-step guide to implementing the algorithm in their programs. However, before attempting to implement the algorithm, readers will need to have a good grasp of the C++ programming language, the quicksort algorithm, and basic multithreading concepts.

C++ is a versatile, high-performance programming language used for developing software applications. Its static typing requires that variable types be declared at the time of declaration, and it is known for its efficiency and performance.

Quicksort is a sorting algorithm that partitions an array into two sub-arrays based on a pivot value and recursively sorts each sub-array. The pivot value is usually chosen as the last element in the sub-array, and the partitioning places all elements smaller than the pivot in the left sub-array and all elements larger than the pivot in the right sub-array.

Multithreading enables a program to perform multiple tasks concurrently, and each thread executes its own set of instructions independently. Multithreading can be used to improve performance in applications that have independent tasks.

To implement the multithreaded quicksort algorithm in C++, readers must understand each of these concepts in-depth. For example, readers must know how to declare variables in C++, write recursive functions to sort sub-arrays, and create and manage threads. The article will provide a detailed explanation of each of these topics and how they relate to the implementation of the multithreaded quicksort algorithm. Here's an example of a C++ function that implements the quicksort algorithm.

void quicksort(int* arr, int left, int right) {
    int i = left;
    int j = right;
    int tmp;
    int pivot = arr[(left + right) / 2];
 
    /* partition */
    while (i <= j) {
        while (arr[i] < pivot)
            i++;
        while (arr[j] > pivot)
            j--;
        if (i <= j) {
            tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
            i++;
            j--;
        }
    };
 
    /* recursion */
    if (left < j)
        quicksort(arr, left, j);
    if (i < right)
        quicksort(arr, i, right);
}

In a multithreaded implementation of this function, each recursive call to quicksort() would be executed in a separate thread. This can significantly improve performance on multi-core CPUs, as each thread can be scheduled to run on a different core. However, care must be taken to ensure that the threads don't interfere with each other by accessing the same memory locations simultaneously. This can be done using synchronization mechanisms like mutexes or semaphores.

Here's a step-by-step guide to implementing multithreaded quicksort algorithm in C++:

• Include Required Libraries:

First, include the required C++ libraries for the implementation of multithreaded quicksort algorithm. These libraries are iostream, algorithm, and thread.

#include <iostream>
#include <algorithm>
#include <thread>

• Implement Partitioning:

To divide the input list into smaller sub-lists, we need to implement the partitioning logic. The partition function takes an input list, selects a pivot element, and rearranges the elements such that all the elements smaller than the pivot are on the left side of the pivot, and all the elements greater than the pivot are on the right side of the pivot.

int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] <= pivot) {
            i++;
            std::swap(arr[i], arr[j]);
        }
    }
    std::swap(arr[i + 1], arr[high]);
    return (i + 1);
}

• Implement Quick Sort Algorithm:

Next, implement the quicksort algorithm which recursively calls itself on the sub-lists created by the partition function.

void quicksort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        std::thread left_thread(quicksort, arr, low, pi - 1);
        std::thread right_thread(quicksort, arr, pi + 1, high);
        left_thread.join();
        right_thread.join();
    }
}

• Implement Multithreading:

To implement multithreading in the quicksort algorithm, we create threads to work concurrently on sorting different sub-lists of the input list. In C++, we can create threads using the std::thread class.

Here's an example of implementing multithreading in the quicksort algorithm using two threads to sort the left and right sub-lists independently:

void quicksort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        std::thread left_thread(quicksort, arr, low, pi - 1);
        std::thread right_thread(quicksort, arr, pi + 1, high);
        left_thread.join();
        right_thread.join();
    }
}

In this code snippet, the first step is to partition the input list to obtain the pivot element pi. Next, two threads are created to independently sort the left and right sub-lists. The left sub-list is sorted recursively by calling the quicksort function with low and pi - 1 as the new range. Similarly, the right sub-list is sorted by calling quicksort with pi + 1 and high as the new range.

Once the threads are created, the join() function is used to wait for them to finish execution before returning the sorted sub-lists. This ensures that the sorted sub-lists are merged only after both threads have completed their respective sorting tasks.

Overall, by implementing multithreading in the quicksort algorithm, we can improve the algorithm's performance on large input lists by dividing the work among multiple threads that can work concurrently.

Complexity Analysis

When analyzing the time and space complexity of an algorithm, we are interested in understanding how the performance of the algorithm scales with the input size. This is important for assessing the efficiency of the algorithm and predicting its performance for large inputs.

In the case of the multithreaded quicksort algorithm, we can analyze its time complexity by considering the number of comparisons and swaps performed on the input data, as well as the number of threads used. The worst-case time complexity of the quicksort algorithm is O(n^2), but with proper pivot selection and partitioning, the expected time complexity can be reduced to O(n log n). The use of multiple threads in the multithreaded quicksort algorithm can further improve the algorithm's performance by enabling parallel processing of the sub-lists, reducing the overall execution time. The time complexity of the multithreaded quicksort algorithm can be expressed as O(n log n / p), where n is the input size and p is the number of threads used.

The space complexity of the multithreaded quicksort algorithm is also important to consider. Space complexity refers to the amount of memory required by the algorithm to perform its operations. In the case of the multithreaded quicksort algorithm, the space complexity is determined by the maximum depth of the recursion stack, which is proportional to the logarithm of the input size. Therefore, the space complexity of the algorithm is O(log n).

When comparing the multithreaded quicksort algorithm with other sorting algorithms, such as bubble sort or insertion sort, we can consider both time and space complexity. For example, bubble sort has a worst-case time complexity of O(n^2), while insertion sort has a worst-case time complexity of O(n^2) and a space complexity of O(1). In comparison, the multithreaded quicksort algorithm has a better expected time complexity of O(n log n / p) and a space complexity of O(log n).

#include <iostream>
#include <thread>
#include <algorithm>
#include <vector>

using namespace std;

const int NUM_THREADS = 4;

template <typename Iterator>
void quicksort(Iterator begin, Iterator end) {
    if (begin == end) return;
    auto pivot = *std::next(begin, std::distance(begin, end) / 2);
    Iterator middle1 = std::partition(begin, end, [pivot](const auto& em){ return em < pivot; });
    Iterator middle2 = std::partition(middle1, end, [pivot](const auto& em){ return !(pivot < em); });

    std::thread threads[NUM_THREADS];
    int thread_num = 0;
    if (std::distance(begin, middle1) > 10000) {
        threads[thread_num++] = std::thread(quicksort<Iterator>, begin, middle1);
    } else {
        std::sort(begin, middle1);
    }
    if (std::distance(middle2, end) > 10000) {
        threads[thread_num++] = std::thread(quicksort<Iterator>, middle2, end);
    } else {
        std::sort(middle2, end);
    }

    for (int i = 0; i < thread_num; i++) {
        threads[i].join();
    }
}

int main() {
    vector<int> nums = {3, 5, 1, 4, 2};
    quicksort(nums.begin(), nums.end());
    for (const auto& num : nums) {
        cout << num << " ";
    }
    cout << endl;
    return 0;
}

This code implements a parallel version of the quicksort algorithm using multiple threads. The quicksort() function takes an iterator to the beginning and end of the range to be sorted. It first selects a pivot element from the middle of the range and partitions the range into two sub-ranges, with one sub-range containing elements smaller than the pivot and the other sub-range containing elements greater than or equal to the pivot.

The code uses std::partition() function from the <algorithm> library to perform this partitioning operation. After partitioning, the function creates up to four threads to sort the two sub-ranges in parallel. If either sub-range is less than 10,000 elements long, it is sorted sequentially using the std::sort() function instead of being sorted concurrently using a separate thread. This is because creating a thread for a small sub-range would result in more overhead than benefit from parallelism.

The std::thread class is used to create and manage the threads that sort the sub-ranges in parallel. The number of threads is set to a constant NUM_THREADS, which can be adjusted depending on the available hardware resources. The threads array holds the thread objects, and thread_num keeps track of the number of threads created. Once all threads have been created, the function waits for each thread to complete using the join() function.

Finally, the sorted sub-ranges are merged to produce the final sorted range. The main function initializes a vector of integers, calls the quicksort() function on it, and then prints out the sorted result.

In summary, complexity analysis is an important tool for evaluating the efficiency of algorithms, and comparing them to other algorithms. In the case of the multithreaded quicksort algorithm, proper analysis of its time and space complexity can help to optimize its performance and identify potential limitations.

Applications of Multithreaded Quick Sort

Multithreaded Quick Sort has various real-world applications, particularly in industries where large datasets are processed and sorted regularly. Some of the areas where Multithreaded Quick Sort can be applied include finance, healthcare, and data analysis.

In finance, for instance, quick sorting is useful in sorting and analyzing large financial data sets to identify trends and patterns. By using Multithreaded Quick Sort, sorting of large datasets can be done in parallel, reducing the processing time.

In healthcare, Multithreaded Quick Sort can be used in analyzing large medical datasets such as medical records, patient information, and research data. With the help of Multithreaded Quick Sort, healthcare providers can easily sort and analyze this data, helping them to make informed decisions.

Data analysis is another area where Multithreaded Quick Sort can be applied, especially in big data processing. The quick sorting algorithm is useful in processing and sorting massive amounts of data generated from various sources, such as social media, search engines, and e-commerce platforms.

Overall, the use of Multithreaded Quick Sort can lead to improved performance and efficiency in sorting large datasets, making it a useful tool in industries where speed and accuracy are crucial.

Questions and Exercises

Here are some sample questions and exercises that can help test the reader's understanding of the multithreaded quicksort algorithm and its implementation:

What is the purpose of multithreaded quicksort?
Explain the concept of multithreading and how it can improve the performance of quicksort.
What are the prerequisites for implementing multithreaded quicksort?
What is the time complexity of multithreaded quicksort? How does it compare to other sorting algorithms?
Write a C++ code snippet to implement multithreaded quicksort.
Describe a real-world scenario where multithreaded quicksort can be applied to improve performance.
What are some potential pitfalls when implementing multithreaded quicksort? How can they be avoided?

Exercises

Implement multithreaded quicksort in C++ and test it with various input sizes. Compare the running time of your implementation with that of the standard quicksort algorithm.
Modify your implementation of multithreaded quicksort to sort an array of integers in descending order.
Write a C++ program to read a large text file, sort the lines using multithreaded quicksort, and write the sorted lines to a new file.
Implement a parallel version of merge sort and compare its performance with that of multithreaded quicksort.
Identify a real-world application where multithreaded quicksort can be applied, and write a proposal outlining the implementation details, potential challenges, and expected benefits.

Conclusion and Discussion

The article "Multithreaded Quick Sort in C++" provides a comprehensive overview of the multithreaded quicksort algorithm and its implementation in C++. It covers the fundamental concepts of the quicksort algorithm and multithreading, followed by a detailed explanation of the implementation steps for the multithreaded quicksort algorithm.

The article also includes an analysis of the algorithm's time complexity and compares it with other sorting algorithms. Additionally, the article discusses various real-world applications of the algorithm, along with a set of questions and exercises designed to test the reader's understanding of the algorithm.

Overall, the article provides a valuable resource for anyone looking to understand the multithreaded quicksort algorithm and its implementation in C++.

Discussion of the future scope and potential improvements to the algorithm:

While the multithreaded quicksort algorithm is already highly efficient and widely used in various applications, there is always room for improvement. One potential area of improvement is the optimization of the algorithm for specific hardware architectures. Another area of improvement is the integration of the algorithm with other parallel processing techniques such as GPU computing. Additionally, researchers could investigate ways to reduce the memory overhead of the algorithm or find more efficient ways to divide the data among threads. As computing technology continues to evolve, there will always be opportunities to improve the efficiency and performance of the multithreaded quicksort algorithm.

With this article at OpenGenus, you must have the complete of Multithreaded Quick Sort in C++.