Non Deterministic Turing Machines

In this article, we learn about non-deterministic turing machines - a generalization of the standard deterministic turing machine from a uniquely determined sequence of computation steps to several possible sequences of computational steps.

Table of contents.

1. Introduction.
2. A formal definition.
3. Properties of non-deterministic turing machines.
4. The complexity of non-deterministic turing machines.
5. Summary.
6. References.

Introduction.

A turing machine is a theoretical machine that manipulates symbols on a strip of tape according to the rule specified in a table. It is as simple as it sounds but turing machines can simulate any logic of any algorithm.

A non-deterministic turing machine is a generalization of a standard deterministic turing machine, in that, we move from a uniquely determined sequence of computation steps to several possible sequences. Although the set of computable functions f(n) doesn't change, the computational complexity differs between deterministic and non-deterministic turing machines.

A comparison between deterministic and non-deterministic turing machines.

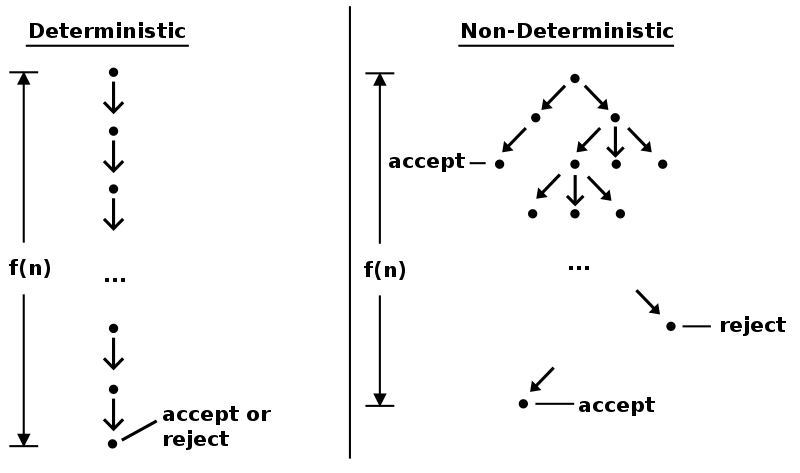
By reducing the amount of computational work from the deterministic paradigm, non-deterministic turing machines pave way for artificially intelligent computing whereby computers learn to solve complex problems and think more like humans.

An example of a non-deterministic turing machine is a probabilistic turing machine whereby an array of actions are determined through a probability distribution. This means that when the machine has more than a single choice, it takes a probabilistic model, analyzes it, and chooses accordingly.

An example of a non-deterministic turing machine model is the following:

• the computer follows paths of logic until an accepted or rejected state is reached then goes back and chooses an action accordingly.

A formal definition.

A non-deterministic turing machine is 6-tuple, that is M= (Q, X, ∑, δ, q0, B, F) where;

• Q is a finite set of states.
• X is the tape alphabet.
• ∑ is the input alphabet.
• δ is a transition function.
• q0 is the initial state.
• B is the blank symbol.
• F is the set of final states.

Properties of non-deterministic turing machines.

The process of computation of a non-deterministic turing machine is interpreted as a deterministic turing machine with the capability to create and start other turing machines processing alternative branches of the calculation. Therefore, a machine T' can simulate a non-deterministic machine T by iterating all branches of the calculation of T up to a specific depth d, after which d is incremented, and the iteration repeats.

The above is done until an accepting branch in the tree is found or no branch can be continued.

Note that this simulation may be infinite since the paths of the tree might not be finite.

Looking at this algorithmically, T' performs a breadth-first search that ensures paths with infinite lengths are handled appropriately.

The complexity of non-deterministic turing machines.

Given a language $\mathrm{L}\subseteq {\mathrm{\Sigma }}^{*}$, we determine the time t(x) needed by a non-deterministic machine to process input x ∈ ${\mathrm{\Sigma }}^{*}$ in the following way;
First, we specify two cases. The case x ∈ L, is defined as the length of the shortest path in the computation tree accepting x.
In another case, x ∉ L, the value of t(x) is defined as the length of the shortest path in the computation tree.

Time t(n) needed by T for processing input x ∈ ${\mathrm{\Sigma }}^{*}$ with the length |x| = n ∈ $\mathbb{N}$ is defined as the maximum of all finite t(x) for x ∈ ${\mathrm{\Sigma }}^{*}$ with |x| = n.

Now, a language $\mathrm{L}\subseteq {\mathrm{\Sigma }}^{*}$ belongs to the complexity class NP since it exists in a non-deterministic turing machine T and a polynom p such that T accepts L wit O(p(|x|)) computation steps for all x ∈ L.

The corresponding complexity class for deterministic machines is P and since these machines are a special case of non-deterministic machines, it holds that P ⊆ NP.
Whether the above statement can be strengthened to P = NP is an open problem in computer science.

Summary.

Reducing the amount of computational work from the deterministic paradigm allows non-deterministic turing machines to pave way for artificially intelligent computing whereby computers learn to solve complex problems and think more like humans.
A non-deterministic turing machine is a generalization of a standard deterministic turing machine from a uniquely determined sequence of computation steps to several possible sequences.

With this article at OpenGenus, you must have the complete idea of Non Deterministic Turing Machines.