Pumping Lemma in Theory of Computation is a theorem that is used to determine if a given string is in a regular language L or a Context Free Language (CFL). We have explained the theorem in depth and presented problems that can be solved using the theorem.

The Pumping theorem has two different variants, one for Regular Language and other for Context Free Language. Pumping Lemma for Context Free Language is a complicated version.

Table of contents:

1. Pumping Lemma for Regular Languages (with proof)
2. Pumping Lemma for Context Free Languages
3. Problems / Application of Pumping Lemma

Let us get started with Pumping Lemma in Theory of Computation.

Pumping Lemma for Regular Languages

The theorem of Pumping Lemma for Regular Languages is as follows:

Given a regular language L.
There exists an integer p (pumping length) >= 1 such that for every string STR in L with length of STR >= p can be written as STR = XYZ provided:

1. y is not null / empty string
2. length of xy <= p
3. for all i >= 0, xyⁱz is a part of L.

In simple terms, a string STR in L can be written in such a form that there are three components (xyz) and if we repeat the middle portion any number of times, the resultant string is also in L.

The name follows from the idea that the middle part of the string is pumped multiple times to form the resultant string.

If this holds true for all string in L, then L is a regular language. Therefore, Pumping Lemma for Regular Languages can be used to find if a given string is in a regular language L and if a given language L is a regular language or not.

Intuitive proof:

If a string STR is long to create a cycle in Deterministic Finite Automata (DFA) for a given regular language L, then we can repeat the cycle (pump) any number of times and form infinite set of strings that will be a part of L as it is represented using the same DFA.

Formal proof:

Let Σ be the alphabet of regular language L. There exists a DFA M = (Q, Σ, δ, q, F) that accepts L. We define p (pumping length) to be the number of states in Q.

Let string STR = s₁s₂ ... s_n such that n >= p.

Let a starting state be r1.

If we take s1 as input at state r1, we move to state r2.

Therefore, if we take s_i as input at state r_i, we move to state r_i+1.

The last / final state is r_n+1.

Number of states in DFA M is p and as n >= p, by pigeonhole principle, we know that there must be a state that repeats itself.

Therefore, there exist i and j such that r_i = r_j.

Therefore, reading characters in a string y will move from state r_i to r_j. Consider the following image to visual DFA M easily.

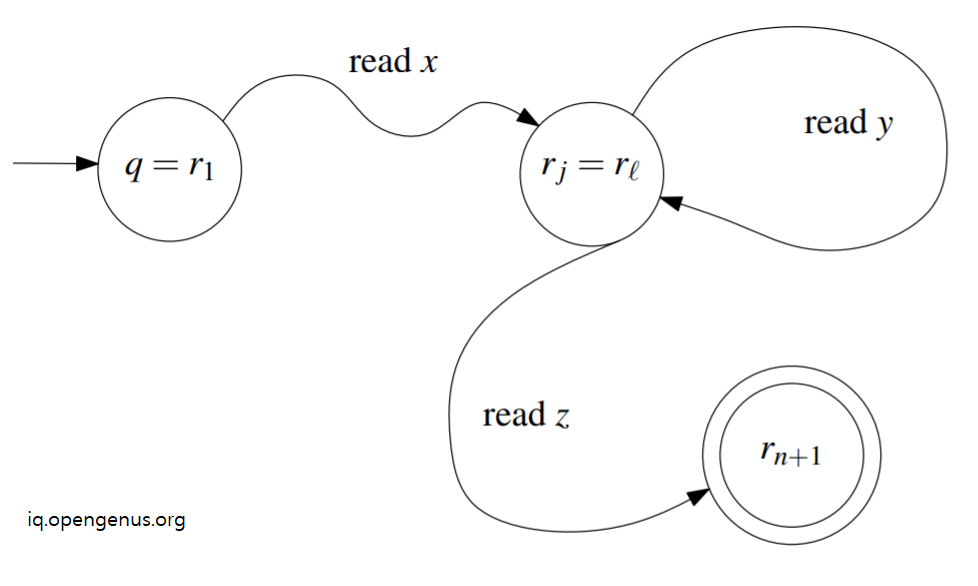
In this view, the string y can be pumped any number of times and the resultant string will stay in DFA M that is in regular language L.

Pumping Lemma for Context Free Languages

The theorem of Pumping Lemma for Context Free Languages is as follows:

Given a Context Free Languages L.
There exists an integer p (pumping length) >= 1 such that for every string STR in L with length of STR >= p can be written as STR = UVWXY provided:

1. VX is not null / empty string
2. length of VWX <= p
3. for all i >= 0, UVⁱXYⁱZ is a part of L.

Note we are pumping two substrings V and Y. In Pumping Lemma for Regular Languages, we were pumping only one substring Y.

Following image will help you understand this theorem:

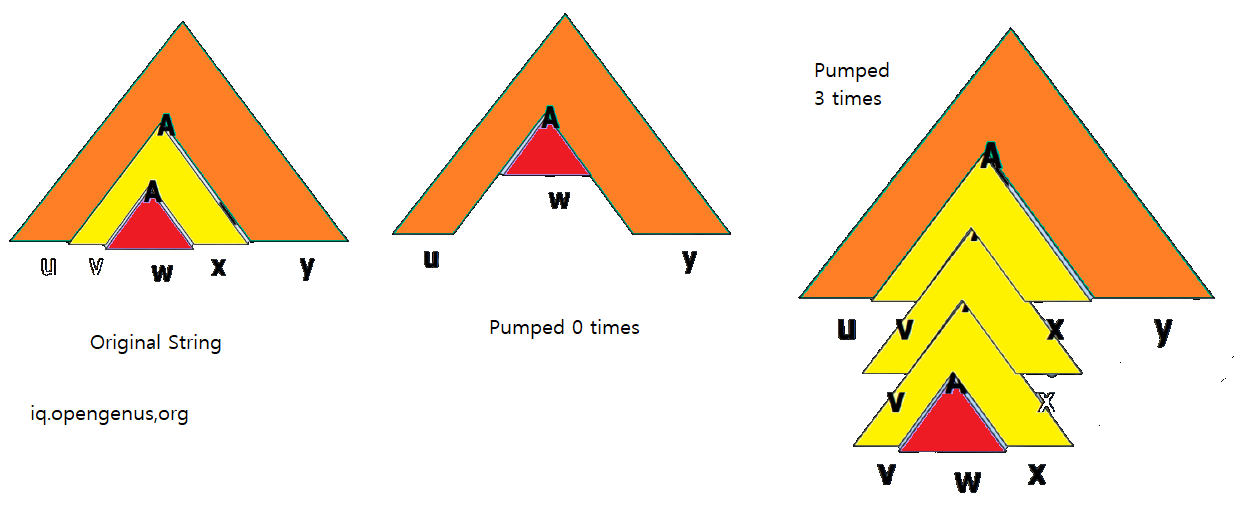
To prove this, you need to have knowledge on Chomsky Normal Form (CNF) and Parse Tree.

Problems / Application of Pumping Lemma

Following are a few problems which can be solved easily using Pumping Lemma. Try them.

Problem 1: Check if the Language L = {w ∈ {0, 1}∗ : w is the binary representation of a prime number} is a regular or non-regular language.

Problem 2: Prove that the Language L = {1ⁿ : n is a prime number} is a non-regular Language.

Problem 3: Let L be the language { 0ⁿ1ⁿ2ⁿ | n >= 1 }. Show that language L is not a Context Free Language.

Problem 4: Show that the Language L = { a ^n! : n >= 0} is not a Context Free Language.

Problem 5: Let L be the language { aⁱb^jc^k | 0 <= i <= j <= k }. Show that this language is not a Context Free Language.

Problem 6: Prove that the language L = = {0ⁿ1ⁿ : n >= 0} is not a regular language.

Problem 7: Prove that the language L = = {0^m1ⁿ : m > n >= 0} is not a regular language.

Problem 8: Let L be the language {ww | w ∈ {0,1}* }. Show that language L is not a Regular Language.

Problem 9: Let L be the language {ww | w ∈ {0,1}* }. Show that language L is not a Context Free Language.

With this article at OpenGenus, you must have complete knowledge of Pumping Lemma in Theory of Computation.