
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Table of contents:
- Introduction
- Basic Principle
- Mathematical Representation
- Interpretation
- Applications
- Variations
- Limitations
- Implications
Introduction
Lotka's law, also known as Lotka-Volterra law of scientific productivity or simply Lotka's law of authorship, is a principle in bibliometrics and information science that describes the distribution of productivity among authors in a particular field. It was formulated by Alfred J. Lotka, an American mathematician and statistician, in the early 20th century.
Lotka's law is typically used to analyze the distribution of scholarly publications or scientific contributions among researchers in a specific academic discipline.
In simple words, Lotka's Law is like a rule for understanding how many articles or papers different authors write in science or academics.
Imagine you have a big group of scientists, and you want to know how many of them write a certain number of articles. Lotka's Law tells us that only a few scientists will write a lot of articles, while most will write only a few.
So, if you think about it like a game, it's like having a small number of superstar players who score lots of goals, and a much larger group of regular players who score fewer goals.
Scientists call this pattern a "power-law distribution," and they use Lotka's Law to figure out how common it is for some people to be super productive and others not so much in the world of academic writing.
Basic Principle
- Lotka's Law focuses on analyzing how the number of authors who have published a certain number of articles is distributed within a given scientific or academic field.
- It highlights the phenomenon that a small percentage of authors contribute significantly more publications compared to the majority of authors who produce fewer papers.
Mathematical Representation
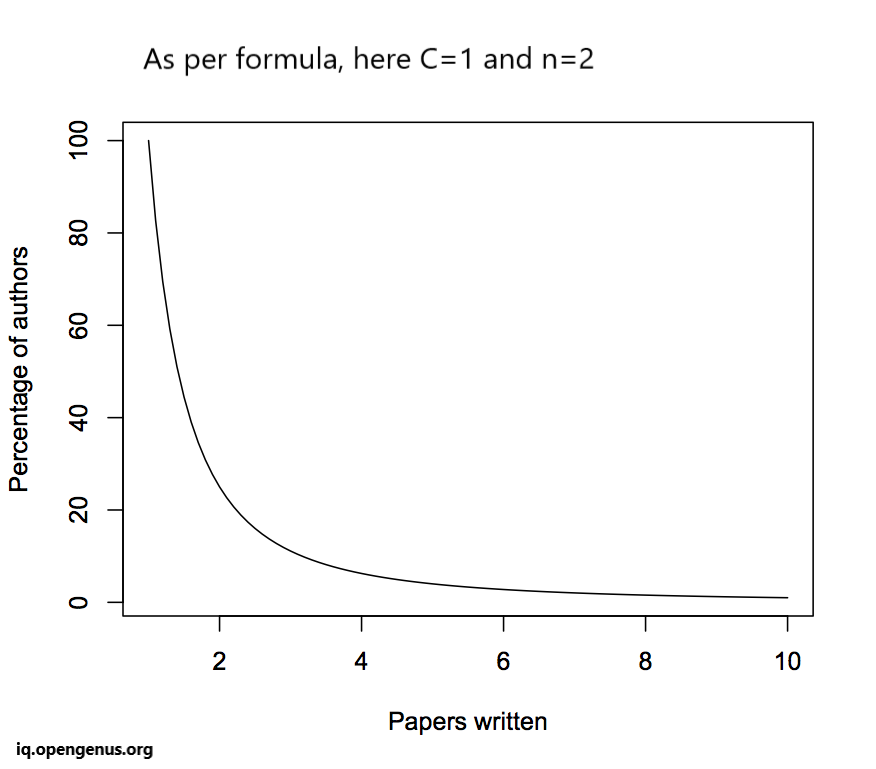
Lotka expressed this relationship mathematically using a power-law distribution. The common representation is:
N(a) = C / (a^n)
- N(a): The number of authors who have published a total of "a" articles.
- C: A constant.
- "n": An exponent typically between 1 and 3, which varies depending on the specific field of study.
Interpretation
- Lotka's Law suggests that the distribution of authors' productivity in academic fields is highly skewed, with a small group of prolific authors and a larger group of less prolific authors.
- The exponent "n" in the power-law distribution determines the degree of skewness. A higher "n" indicates a more concentrated distribution, while a lower "n" implies a less concentrated distribution.
Applications
- Understanding author productivity: Lotka's Law helps researchers and bibliometricians analyze how scientific output is distributed among authors in a particular discipline.
- Collaboration and expertise: It sheds light on patterns of collaboration, as prolific authors may collaborate more, and the distribution of expertise within a field.
Variations
- While the basic concept remains consistent, the specific values of "n" and the constant "C" can vary across different academic fields and time periods.
- Some fields may have a more extreme concentration of prolific authors, while others may exhibit a more balanced distribution.
Limitations
- Lotka's Law provides a simplified model of author productivity and may not capture all nuances of academic publishing.
- It assumes that the distribution remains constant over time, which may not hold true in rapidly evolving fields.
- The law's parameters can be sensitive to data quality and methodology.
Implications :
Lotka's Law has practical implications for understanding the dynamics of authorship in academia, helping institutions and researchers identify prolific contributors and foster collaboration.
