Finite Automata in Theory of Computation

In this article, we discuss finite automata, a state machine that takes a regular expression and changes its state accordingly for each literal and when the transitions reach the final state, the string is accepted and thus it is said to be a valid token of a language.

Table of contents.

1. Introduction.
2. Controlling a toll gate.
3. Deterministic finite automata.
4. Non-deterministic finite automata.
5. Similarities between DFA and NFA.
6. Summary.
7. References.

Prerequisites.

1. Mathematical groundwork and proofs

Introduction.

Finite automata is an idealized machine used to recognizing patterns in an input that is taken from a characters set.
Given a string it either accepts it or rejects it. This depends on if the pattern defined in the automata is in the input.
A finite automaton will consists of a set of states, start state, end state and a set of transitions.

Controlling a toll gate.

The above image shows a toll gate that demonstrates how automaton shows up in a natural way.
Let's try to design a computer that controls the toll gate. When a car arrives at the gate it is currently closed and after the car owner pays a sum of money, the gate opens.
The amount for the gate to open is 25 cents. We only have 5, 10 and 25 cents denominations. The gate cannot charge an excess amount.
So to got through a driver will insert a sequence of coins into the machine and it decides to either open the gate or keep it shut.
The machine will therefore have the following six states:

• q0 the state whereby it has not collected any coins
• q1 if it has only collected 5 cents
• q2 if it has collected 10 cents
• q3 if it has collected 15 cents
• q4 if it has collected 20 cents
• q5 if it has collected 25 cents or more

Assuming a driver initiates a sequence (10, 5, 5, 10), the machine switches as follows:

• It receives 10 cents and switches from q0 to q2.
• It receives 5 cents and switches from q2 to q3.
• It receives 5 cents again and switches from q3 to q4.
• It receives 10 cents again and switches from q4 to q5, then the gate opens.

Here is the machine's behavior for all possible machine sequences.

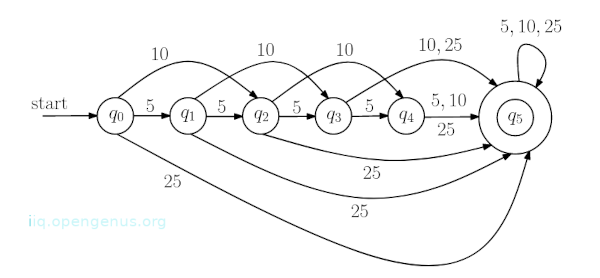
q5 is a special state since when the machine reaches this state the gate opens.
At any point the machine only has to remember what state it is in and thus this needs little memory, that is, ⌈log 6⌉ = 3 bits of memory.

Deterministic finite automata

Consider the image below. Given an input string 1101, it is processed as follows.

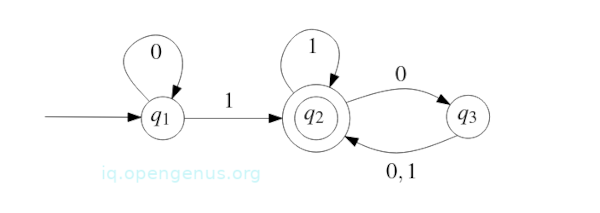
q1 is the starting state, q2 is the accepting state.

• To begin, the machine is at state q1.
• It reads 1 and switches to state q2.
• It reads 1 again and switches to state q2(doesn't switch).
• It reads 0 and switches to state q3.
• It reads 1 and switches to state q2.

After the string is processed, the machine is in the accept state q2 and thus we say the string is accepted by the machine.

Consider the string 0101010, and try visualizing how it will be processed, you will see that it puts the machine in state q3 which is not the accept state and we say that the string is rejected by the machine.

So what kinds of strings does this machine accept?

• binary strings ending in 1.
• binary strings with an even number of 0s following the rightmost 1.

Every other string is rejected.

Finite automaton

This is a 5-tuple M = (Q,Σ, δ, q, F) where

• Q is a finite set whose elements we refer to as states.
• Σ is a finite set known as the alphabet and whose elements are referred to as symbols.
• δ : Q × Σ → Q which is a function known as the transition function.
• q is an element of Q known as the start state.
• F is a subset of Q, its elements are referred to as accept states.

Think of the transition function δ as a program of the finite automaton M = (Q,Σ, δ, q, F). This function tells us what M can do on a single step.

• Let r be a state Q and a a symbol of the alphabet Σ, If the finite automaton M is in r state and reads the symbol a, it will switch from state r to state δ(r, a).

From the toll gate example machine we designed we have Q = {q0, q1, q2, q3, q4, q5}, Σ ={5, 10, 25}, the start state as q0, F = {q5} and δ is given by the table below;

	5	10	25
q0	q1	q2	q5
q1	q2	q3	q5
q2	q3	q4	q5
q3	q4	q5	q5
q4	q5	q5	q5
q5	q5	q5	q5

And from the string example, Q={q1, q2, q3}, Σ ={0,1}, the start state is q1, F = {q2} and δ is given by the table below:

	0	1
q1	q1	q2
q2	q3	q2
q3	q2	q2

Nondeterministic finite automata.

Let's learn about non-deterministic finite automata through an example where we shall see the difference between the two.

An Example:
Consider the state diagram below:

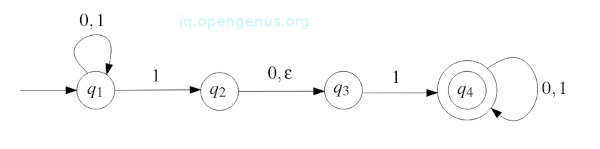
Note the following differences:

• If the automaton is at state q1 and reads the symbol 1, it will have two options, the first is to stay in state q1 or switch to state q2.
• If the automaton is in state q2, it can switch to q3 without reading a symbol which is indicated by the edge with an empty string ε.
• Finally, if the automaton is in state q3 and reads 0, it can't continue.

Given the string 010110 as input, here are the states:

• The start state is q1.
• The start symbol is 0 and thus the automaton doesn't switch states and stays in q1.
• Next we have 1, the automaton chooses to either switch to q2 or stay at q1. If it stays in q1, it will still be in this state after reading the third symbol otherwise If it switches to q2, it will have another two options which are: (1.) To read the third symbol which is 0 and switch to q3 or (2.) Switch to q3 without reading third symbol.

If this continues we have seven possible computations as shown in the image below;

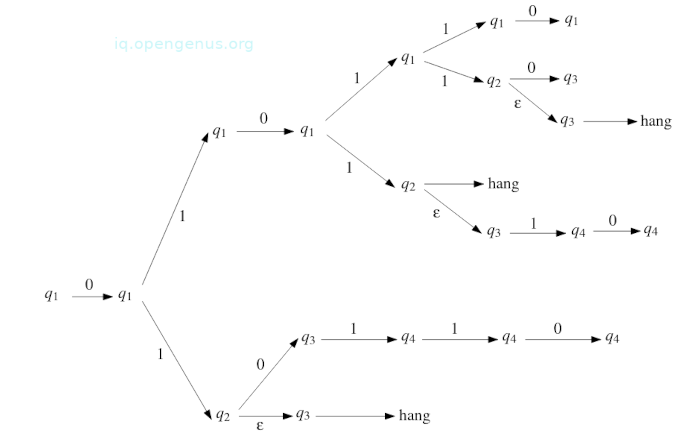
Let's look at the lowest path:

• Reading the first symbol the automaton stays in q1 state.
• After reading the second symbol, it switches to q2
• It doesn't read the third symbol but switches to q3 where it can no longer proceed. The third symbol is 0 however there is no edge to leave q3 labeled 0 and so this computation hangs as we can see from the image.

Now, out of the seven computations only two will reach the accept state - q4 and therefore we state that the automaton accepts the string 010110 because there is at least once computation ending in the accept state.

Given another string 010, we have the following three computations.

1. q1 $\stackrel{0}{\to }$ q1 $\stackrel{1}{\to }$ q1 $\stackrel{0}{\to }$ q1
2. q1 $\stackrel{0}{\to }$ q1 $\stackrel{1}{\to }$ q2 $\stackrel{0}{\to }$ q3
3. q1 $\stackrel{0}{\to }$ q1 $\stackrel{1}{\to }$ q2 $\stackrel{\mathrm{\epsilon }}{\to }$ q3 → hang

None of the computations end in accept state and therefore the string is rejected.

In conclusion Non-deterministic Finite Automata accept a string if there exists at least a path that:

• Starts in the start state
• Does not hang before the entire string has been read
• Ends in an accept state

A string is rejected if none of the conditions hold.

Similarities between DFA and NFA.

Although it may seem that NFAs are powerful than DFAs this is not the case as we shall see her.
Here we prove that a language is only accepted by DFA iff it is accepted by NFA.
For this we will first learn how to convert an arbitrary NFA to a DFA that accepts the same language.
Let's now go about converting DFA to NFA.
Let M = (Q,Σ, δ, q, F) be a DFA. δ is a function δ : Q × Σ → Q and so we define δ′ : Q × Σε → P(Q) as follows. For any r ∈ Q and for any a ∈ ${\mathrm{\Sigma }}_{ϵ}$

${\mathrm{\delta }}^{\text{'}}(\mathrm{r}, \mathrm{a})$ = {$\left\{\begin{array}{ll}\mathrm{\delta }\{(\mathrm{r}, \mathrm{a})\}& \mathrm{if} \mathrm{a} \ne \mathrm{ϵ}\\ \varnothing & \mathrm{if} \mathrm{a} = \mathrm{ϵ}\end{array}\right.$

Therefore, N = (Q,Σ, δ′, q, F) is an NFA whose behavior will be exactly the same as that of DFA M.
We can see this by looking at the state diagrams of M and N and we see that they are equal and therefore L(M) = L(N).

Now to convert and NFA to DFA.
Theorem: Let N = (Q,Σ, δ, q, F) be a non-deterministic finite automaton(NFA). There exists a deterministic finite automaton M such that L(M) = L(N).

Proof: Keep in mind that NFA N can perform multiple computations on an input string and therefore the idea of the proof is to construct a DFA M which runs all these computations simultaneously.
DFA M will have the property below:

• The state in which M is in after reading the initial part of the input string will correspond exactly to the set of all states N can reach after reading the same part of the input string.

We present the conversion for the case when N doesn't contains ϵ-transitions. In other words, Ns state diagram doesn't contain an edge with ϵ as a label.
Lets define DFA of M as M = (Q′,Σ, δ′, q′, F′) where:

• The set Q′ of states is equal to Q′ = P(Q); observe |Q′| = $2^{\left|\mathrm{Q}\right|}$.
• The start state q′ is equal to q′ ={q} and therefore M has a similar start state as N.
• The set F′ of accept states is equal to the set of all elements R of Q′ with the property that R contains at least on state that accepts, that is,
  F′ = {R ∈ Q′ : R ∩ F ≠ ∅}
• The transition function δ′ : Q′ × Σ → Q′ is defined as follows, for each R ∈ Q′, for each a ∈ Σ,
  ${\mathrm{\delta }}^{\text{'}}(\mathrm{r}, \mathrm{a})=\underset{\mathrm{r}\in \mathrm{R}}{\cup }\mathrm{\delta }(\mathrm{r}, \mathrm{a})$

Looking at the transition function δ′ we see that N is an NFA, δ(r, a) is a subset of Q and therefore this implies that δ′(R, a) is the union of the subsets Q and also a subset of Q.
Thus δ′(R, a) is an element of Q′.
Set δ(r, a) is equal to the set of all states of NFA N that can be reached from state r by reading the symbol a.
We take the union of sets δ(r, a), where r ranges over all R elements, to get the new set δ′(R, a). This new set is the state that DFA M reaches from R state by reading symbol a.
Here we have obtained a correspondence given when we began this proof.
Consider the general case where we allow ϵ-transitions in NFA N.
DFA M is defined the same as however in this case the start state q′ and the transition function δ' have to be modified.

Remember the NFA computation consists of:

1. Start in state q and make zero or more ϵ-transitions
2. Read a real symbol of Σ and move to a new state or stay in the current state
3. Make zero or more ϵ-transitions
4. Read a real symbol of Σ and move to a new state or stay in current state
5. Make zero or more ϵ-transitions
6. And so on

DFA M will simulate this in the following way:

• It simulates (1) in a single step, As we will see shortly, this simulation is implicitly encoded in the definition of the start state q′ of M
• It simulates (2) and (3) in a single step
• It simulates (4) and (5) in a single step
• An so on

In a single step DFA M simulates a reading of one real symbol Σ, followed by making zero or more ϵ-transitions.
We formalize this using the concept of ϵ-closure whereby for any state r of NFA N, the ϵ-closure of r denoted by ${\mathrm{C}}_{\mathrm{ϵ}}\left(\mathrm{r}\right)$ is defined to be the set of all states of N that can be reached from r by making zero or more ϵ-transitions.

For any state R of DFA M ${\mathrm{C}}_{\mathrm{ϵ}}\left(\mathrm{R}\right)=\underset{\mathrm{r}\in \mathrm{R}}{\cup }{\mathrm{C}}_{\mathrm{ϵ}}\left(r\right)$.

To define the transition function δ′ of DFA M, assume M is in state R and reads the symbol a
Here, NFA N would have been in any state r of R.
By reading the symbol a, N can switch to any state in δ(r, a), then make zero or more ϵ-transitions.
Therefore, the NFA can switch to any state in the set ${\mathrm{C}}_{\mathrm{ϵ}}\left(\mathrm{\delta }(\mathrm{r}, \mathrm{a})\right)$ and based on this we define δ′(R, a) to be,
${\mathrm{\delta }}^{\text{'}}(\mathrm{R}, \mathrm{a})=\underset{\mathrm{r}\in \mathrm{R}}{\cup }{\mathrm{C}}_{\mathrm{ϵ}}\left(\mathrm{\delta }\right(\mathrm{r}, \mathrm{a}\left)\right)$

In summary, NFA N = (Q,Σ, δ, q, F) is converted to DFA M= (Q′,Σ, δ′, q′, F′) where:

• Q′=P(Q),
• q′= ${\mathrm{C}}_{\mathrm{ϵ}}$({q}),
• F′={R ∈ Q′ : R ∩ F ≠ ∅},
• δ′ : Q′ × Σ → Q′, defined as follows, for each R ∈ Q′ and for each a ∈ Σ
  ${\mathrm{\delta }}^{\text{'}}(\mathrm{R}, \mathrm{a})=\underset{\mathrm{r}\in \mathrm{R}}{\cup }{\mathrm{C}}_{\mathrm{ϵ}}\left(\mathrm{\delta }\right(\mathrm{r}, \mathrm{a}\left)\right)$

The results obtain are summarized in the following theorem;
Theorem: Let A be a language, then A is regular if and only if there exists a non-deterministic finite automaton that accepts A.

Summary.

Every non-deterministic finite automaton can be converted into its equivalent deterministic finite automaton.

Finite automata has two states namely, accept state and reject state. The accept state is arrived at when an input string is processed successfully.
During a transition an automata either decides to proceed to the next state or not.

References.

1. Context Free Languages