
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes
Pairing heaps are a type of heap data structures which have fast running time for their operations. They are modificaton of Binomial Heap. Basically it is a type of self adjusting Binomial Heap which adjusts or rearrange themselves during the operations, due to which they remain balanced.
A pairing heap would either be an empty heap, or a pairing tree consisting of a root element and a list of pairing heaps(which may be empty). Pairing heaps maintain a min-heap property i.e. all parent nodes have smaller value than their children.
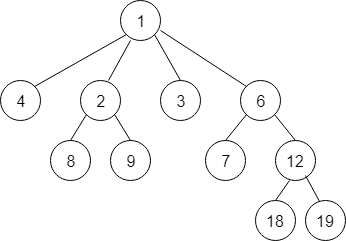
Each Node consists following information:
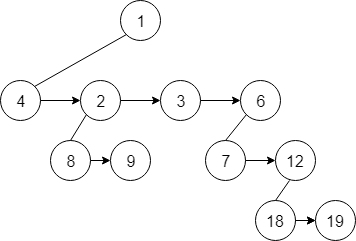
- A pointer to its leftmost child node
- A pointer to its sibling nodes.
Following is the diagram which shows the pointers in pairing heap.
Basic Operations
- Merge : Merge two pairing heaps.
- Find Minimum : Find the minimum element from pairing heap
- Insert : Insert a new element
- Extract Minimum : Delete the minimum element from pairing heap
Merge
Merge functions takes two pairing heap as input, A and B, and returns a pairing heap that contains all elements of A and B.
Pseudocode
function merge(heap1, heap2)
if heap1 == Empty
return heap2
elsif heap2 == Empty
return heap1
elsif heap1.elem < heap2.elem
return Heap(heap1.elem, heap2 :: heap1.subheaps)
else
return Heap(heap2.elem, heap1 :: heap2.subheaps)
Example:
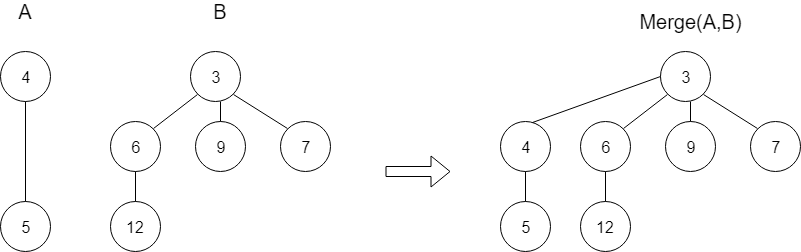
- If merge operation occurs between a non-empty heap and an empty heap, then merge function would just return that non-empty heap.
- And if both heaps are non-empty, then it would return a heap where the root of merged heap would be smallest root of two heaps.
Find Minimum
Find Minimum function would return the minimum element of the heap.
Finding minimum element is pretty easy. We just need to get the top element of the heap.
Pseudocode
function findMin(heap)
if heap == Empty
error
else
return heap.elem
Insertion
Insert function will insert an element in the existing pairing heap.
Merge Operation will be used for insertion operation.
Pseudocode
function insert(elem, heap)
return merge(Heap(elem, []), heap)
- Inserting an element is similar to merging the element in the heap, or merging two heaps(one of them have single element).
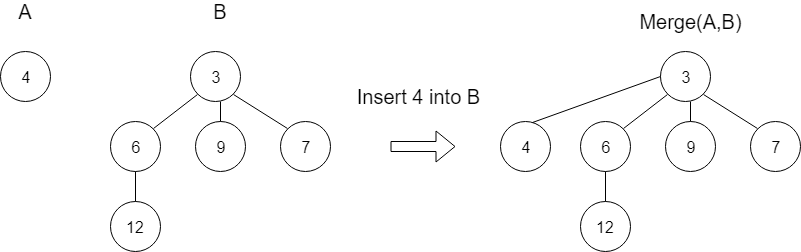
Extract Minimum
Basically, in a pairing heap(min-heap) the smallest element is it's root node. So for deletion of smallest element, deletion of root node should be done.
- If the root has two or more than two subtrees, then these subtress must be merged together into a singke tree after deletion of root node.
- But we don not have pointers to both the subtrees, so may be a deletion of minimum can cause violation in min-heap property. And to solve this we will use two-pass merge.
- Initially, two-pass pairing moves left to right merging pair of trees, and then on seconnd pass it moves right to left and merges the rightmost subtree with the remaining subtrees.
Pseudocode
function extractMin(heap)
if heap == Empty
error
else
return merge-pairs(heap.subheaps)
function merge-pairs(l)
if length(l) == 0
return Empty
elsif length(l) == 1
return l[0]
else
return merge(merge(l[0], l[1]), merge-pairs(l[2.. ]))
Implementation
#include <iostream>
#include <cstdlib>
#include <vector>
using namespace std;
class PairNode {
int element;
PairNode *leftChild;
PairNode *nextSibling;
PairNode *prev;
PairNode(int element) {
this->element = element;
leftChild = NULL;
nextSibling = NULL;
prev = NULL;
}
};
class PairingHeap {
PairNode *root;
void compareAndLink(PairNode * &first, PairNode *second);
PairNode *combineSiblings(PairNode *firstSibling);
PairingHeap();
PairingHeap(PairingHeap &rhs);
bool isEmpty();
bool isFull();
int &findMin();
PairNode *Insert(int &x);
void deleteMin();
void deleteMin(int &minItem);
};
PairingHeap() {
root = NULL;
}
PairingHeap(PairingHeap & rhs) {
root = NULL;
*this = rhs;
}
PairNode Insert(int &x) {
PairNode *newNode = new PairNode(x);
if (root == NULL)
root = newNode;
else
compareAndLink(root, newNode);
return newNode;
}
int findMin() {
return root->element;
}
void deleteMin() {
PairNode *oldRoot = root;
if (root->leftChild == NULL)
root = NULL;
else
root = combineSiblings(root->leftChild);
delete oldRoot;
}
void deleteMin(int &minItem) {
if (isEmpty()) {
cout<<"The Heap is Empty"<<endl;
return;
}
minItem = findMin();
deleteMin();
cout<<"Minimum Element: "<<minItem<<" deleted"<<endl;
}
bool isEmpty() {
return root == NULL;
}
bool isFull() {
return false;
}
void compareAndLink(PairNode * &first, PairNode *second) {
if (second == NULL)
return;
if (second->element < first->element) {
second->prev = first->prev;
first->prev = second;
first->nextSibling = second->leftChild;
if (first->nextSibling != NULL)
first->nextSibling->prev = first;
second->leftChild = first;
first = second;
}
else {
second->prev = first;
first->nextSibling = second->nextSibling;
if (first->nextSibling != NULL)
first->nextSibling->prev = first;
second->nextSibling = first->leftChild;
if (second->nextSibling != NULL)
second->nextSibling->prev = second;
first->leftChild = second;
}
}
PairNode combineSiblings(PairNode *firstSibling) {
if (firstSibling->nextSibling == NULL)
return firstSibling;
static vector<PairNode *> treeArray(5);
int numSiblings = 0;
for (; firstSibling != NULL; numSiblings++)
{
if (numSiblings == treeArray.size())
treeArray.resize(numSiblings * 2);
treeArray[numSiblings] = firstSibling;
firstSibling->prev->nextSibling = NULL;
firstSibling = firstSibling->nextSibling;
}
if (numSiblings == treeArray.size())
treeArray.resize(numSiblings + 1);
treeArray[numSiblings] = NULL;
int i = 0;
for (; i + 1 < numSiblings; i += 2)
compareAndLink(treeArray[i], treeArray[i + 1]);
int j = i - 2;
if (j == numSiblings - 3)
compareAndLink (treeArray[j], treeArray[j + 2]);
for (; j >= 2; j -= 2)
compareAndLink(treeArray[j - 2], treeArray[j] );
return treeArray[0];
}
int main()
{
int choice, num, pos, minimumElement;
char ch;
PairingHeap h;
PairNode * pn;
while (1) {
cout << "1.Insert Element"<< endl;
cout << "2.Extract Minimum Element " << endl;
cout << "3.Find Minimum"<< endl;
cout << "4.Quit"<< endl;
cout << "Enter your choice : ";
cin >> choice;
switch(choice) {
case 1:
cout << "Enter the number to be inserted : ";
cin >> num;
pn = h.Insert(num);
break;
case 2:
h.deleteMin(num);
break;
case 3:
minimumElement = h.findMin();
cout << "Minimum Element is " << minimumElement << endl;
break;
case 4:
exit(1);
default:
cout<<"Wrong choice"<<endl;
}
}
return 0;
}
Time Complexity
- Merge : O(log N)
- Find Minimum : O(1)
- Insertion : O(1)
- Extract Minimum : O(log N)
Applications
- Efficient implementation of prority queue.
- They are faster than binary heaps and Fibonacci heaps.
- Least Time Complexity in most of the operations.
- Can be used as an efficient way for implementing Dijsktra's Algorithm.
