
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes | Coding time: 15 minutes
In this type of segment tree we introduce persistency in our segment trees which means retaining the older versions. Persistency means to store multiple versions of the data structure based on the modifications done on it. It can be seen as what Git version control system does.
Persistant data structures behave like Git
While it may be easy to store multiple versions as separate instances, it becomes a significant overhead in terms of memory and time complexity. Our aim is to introduce persistency in segment trees but also ensure that the space and time complexity is not affected.
This brings in a whole new power to already powerful segment trees.
Basic Idea
For each change in the initial segment tree we will create a new version of it.Let us consider the initial version as version-0 and so the new versions will be version 1,2,3..... .But creating a new segement tree for every change will take O(nlogn) time and space which we cannot afford.
To avoid extra time and space we give a basic thought i.e. for every point update in the present segment tree only log(n) nodes have to be moified,so we only create these log(n) nodes and share rest of the tree from the previous version of the tree.
Example
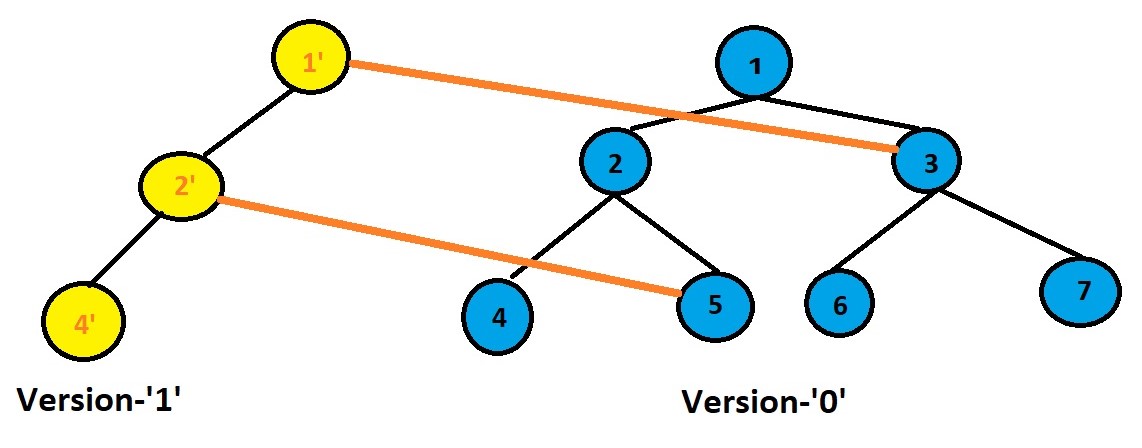
In the diagram given below if we do a point update on node 4 it will be reflected in node 2 and node 1.Therefore the affected nodes will be node 1,node 2 and node 4.
Now version 1 of the segment tree will have node 1' which will have node-3 as its right child as it is unaffected by the point update.The affected node is node-2,so we create a new node node-2' and make that the left child of node-1' .
Now node-2' we will have node-5 as it's right child but node-4' as the new left child as we have updated node-4.Rest of the nodes will be shared by this version.
Problem statement
Given an array A[] and different point update operations.
Considering each point operation to create a new version of the array. We need to answer the queries of type:
Q v l r : output the sum of elements in range l to r just after the v-th update.
Approach
We have to keep track of only the root nodes of newly created version,for this purpose we make an array of pointers to the root nodes of all the versions.Then for each range sum query we will pass the required version’s root node in our query function and output the required sum.
Three basic functions are used to implement persistent segment trees namely-:
- Build
- Upgrade
- Query
Build operation
Build()-This function takes pointer to root node,lowest and highest index as parameters.In this function we construct the version-0 segment tree using bottom up recursion technique. In this case we are building a range addition segment tree.
Pseudocode:
void build(node* n,int low,int high)
{
if (low==high)
{
n->val = arr[low];
return;
}
int mid = (low+high) / 2;
n->left = new node(NULL, NULL, 0);
n->right = new node(NULL, NULL, 0);
build(n->left, low, mid);
build(n->right, mid+1, high);
n->val = n->left->val + n->right->val;
}
Upgrade operation
Upgrade()-This function takes pointer to previous root node ,pointer to the current root node, lowest index, highest index, index at which value is to be updated as parameters. Now using recursion we start finding the nodes which will be affected by the updation and then update those nodes in the next version but make links of the newly created nodes with the children of older nodes which were not affected to reduce space complexity. At last we fill the current node with the sum of it's children.
Example- In the above diagram if node-4 of version-0 is to be updated then using recursion we first reach the node and create a new node-4' and then update it with value and then traverse to node-2' and then make node-5 as it's right child and node-4' as it's left child and update it's value by taking sum of both the nodes.Then we traverse to node-1' and make node-3 as it's right child and node-2' as it's left child and update it's value by taking sum of both the nodes.
Pseudocode:
//Creates new version of intial segment tree
//node*prev is pointer to the previous version node
//node*cur is pointer to the current version node
//low is the lowest index i.e. '0'
//high is the highest index i.e. 'n-1'
//idx is the index at which point update is done
//'value' is the value to which value at 'idx' is updated
void upgrade(node* prev, node* cur, int low, int high,
int idx, int value)
{
if (idx > high or idx < low or low > high)
return;
if (low == high)
{
// modification in new version
cur->val = value;
return;
}
int mid = (low+high) / 2;
if (idx <= mid)
{
//traverse left subtree
// link to right child of previous version as right subtree is not updated
cur->right = prev->right;
// create new node as it is to be updated
cur->left = new node(NULL, NULL, 0);
upgrade(prev->left,cur->left, low, mid, idx, value);
}
else
{
//traverse right subtree
// link to left child of previous version as left subtree is not affected
cur->left = prev->left;
// create new node as it is yo be updated
cur->right = new node(NULL, NULL, 0);
upgrade(prev->right, cur->right, mid+1, high, idx, value);
}
// calculating data for current version
// by combining previous version and current
// modification
cur->val = cur->left->val + cur->right->val;
}
Query operation
Query()-This function takes root node of the version on which query is to be made lowest index, highest index and index range of the query. Now we have the root node of that particular version and we anwer the range query by traversing the nodes the modified nodes as well as the nodes in the previous version of the tree which give the sum in the given index range.
Example-In the above diagram if we want the sum of index range [0,2] version-1 we first traverse all the down to node-2' as it gives the sum from index range [0,1] and while recursing from the root of version-1 also visit node-6 which given element at index-2 and add this value to the value at node node-2.
Pseudocode:
int query(node* n, int low, int high, int l, int r)
{
if (l > high or r < low or low > high)
return 0;
if (l <= low and high <= r)
return n->val;
int mid = (low+high) / 2;
int p1 = query(n->left,low,mid,l,r);
int p2 = query(n->right,mid+1,high,l,r);
return p1+p2;
}
C++ Implementation-
Following is the C++ implementation of Persistent segment tree:
#include "bits/stdc++.h"
using namespace std;
#define MAX 100
/* data type for individual
* node in the segment tree */
struct node
{
// This field stores value of node
int val;
// This field stores the pointer to left and right child respectively
node* left, *right;
//Constructor
node() {}
node(node* l, node* r, int v)
{
left = l;
right = r;
val = v;
}
};
// input array
int arr[MAX];
//array storing root pointers for all versions
node* version[MAX];
// Construction of Version-0
void build(node* n,int low,int high)
{
if (low==high)
{
n->val = arr[low];
return;
}
int mid = (low+high) / 2;
n->left = new node(NULL, NULL, 0);
n->right = new node(NULL, NULL, 0);
build(n->left, low, mid);
build(n->right, mid+1, high);
n->val = n->left->val + n->right->val;
}
//Creates new version of intial segment tree
//node*prev is pointer to the previous version node
//node*cur is pointer to the current version node
//low is the lowest index i.e. '0'
//high is the highest index i.e. 'n-1'
//idx is the index at which point update is done
//'value' is the value to which value at 'idx' is updated
void upgrade(node* prev, node* cur, int low, int high,
int idx, int value)
{
if (idx > high or idx < low or low > high)
return;
if (low == high)
{
// modification in new version
cur->val = value;
return;
}
int mid = (low+high) / 2;
if (idx <= mid)
{
//traverse left subtree
// link to right child of previous version as right subtree is not updated
cur->right = prev->right;
// create new node as it is to be updated
cur->left = new node(NULL, NULL, 0);
upgrade(prev->left,cur->left, low, mid, idx, value);
}
else
{
//traverse right subtree
// link to left child of previous version as left subtree is not affected
cur->left = prev->left;
// create new node as it is yo be updated
cur->right = new node(NULL, NULL, 0);
upgrade(prev->right, cur->right, mid+1, high, idx, value);
}
// calculating data for current version
// by combining previous version and current
// modification
cur->val = cur->left->val + cur->right->val;
}
int query(node* n, int low, int high, int l, int r)
{
if (l > high or r < low or low > high)
return 0;
if (l <= low and high <= r)
return n->val;
int mid = (low+high) / 2;
int p1 = query(n->left,low,mid,l,r);
int p2 = query(n->right,mid+1,high,l,r);
return p1+p2;
}
int main()
{
int A[] = {5,6,7,8};
int n = sizeof(A)/sizeof(int);
for (int i=0; i<n; i++)
arr[i] = A[i];
// Version-0
node* root = new node(NULL, NULL, 0);
build(root, 0, n-1);
// storing root node for version-0
version[0] = root;
//Creating Version-1 root by initialising it by '0'
version[1] = new node(NULL, NULL, 0);
//Upgrading Version-1
upgrade(version[0], version[1], 0, n-1, 0, 1);
//Creating Version-2 root by initialising it by '0'
version[2] = new node(NULL, NULL, 0);
//Upgrading Version-2
upgrade(version[1],version[2], 0, n-1, 3, 10);
cout << "Version-0 , query(0,2) : ";
cout << query(version[0], 0, n-1, 0, 2) << endl;
cout << "Version-1 , query(0,2) : ";
cout << query(version[1], 0, n-1, 0, 2) << endl;
cout << "Version-2 , query(0,2) : ";
cout << query(version[2], 0, n-1, 0, 2) << endl;
return 0;
}
Output-:
Version-0 , query(0,2) : 18
Version-1 , query(0,2) : 14
Version-2 , query(0,2) : 14
Application of persistent data structures
Basic example where persistence data structures are used is Version Control.
We can branch out from the history and then make updates and again merge it back to the original master root.
Persistent segment trees are basically used where we have to store the previous results and update the tree as well in accordance with the give point update query and give results after k-th update without using any extra time or space.Finding the k-th smallest number in a range is also an application of persistent segment tree.
Question
Create a range minimum persistent segment tree and answer queries on it.
HAPPY CODING!
