Recursive and Recursively Enumerable Languages

In this article, we learn about the properties of recursive and recursively enumerable languages in terms of union, intersection, and complements and compare the two languages.

Table of contents.

1. Introduction.
2. Differences between recursive and recursively enumerable languages.
3. Properties of both recursive and recursively enumerable languages.
4. Summary.
5. References.

Introduction.

When a turing machine T operates on an input string S, there are three outcomes, these are;

• It halts and accepts the string.
• It halts and rejects the string.
• Never halts, proceeds infinitely.

What are Recursive languages.

We refer to a language L as recursive if there exists a turing machine T for it. In this case, the turing machine accepts every string in language L and rejects all strings that don't match the alphabet of L.

In other words, if string S is part of the alphabet of language L, then the turing machine T will accept it otherwise the turing machine halts without ever reaching an accepting state.

Recursively enumerable languages.

Here if there is a turing machine T that accepts a language L, the language in which an enumeration procedure exists is referred to as a recursively enumerable language.

Note that some recursive languages are enumerable and some enumerable languages are recursive.

The relationship between recursive and recursively enumerable languages.

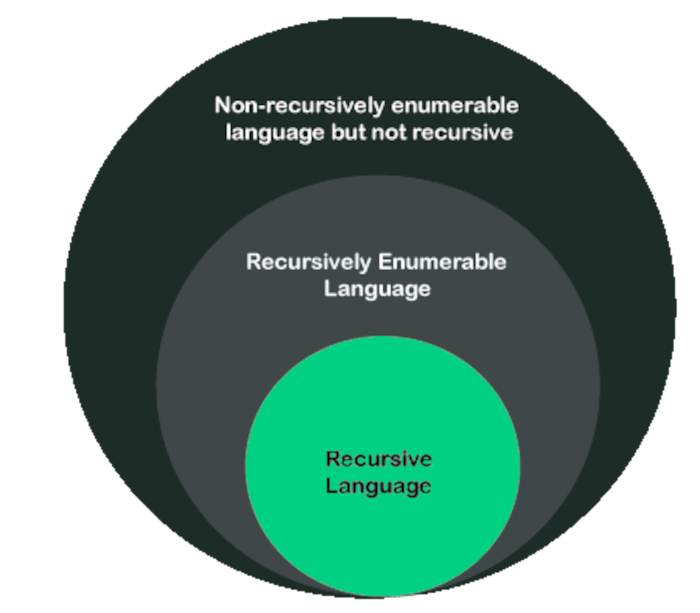
Examples of recursively enumerable languages are;
Recursive languages, Regular languages, Context-sensitive languages, Context-free languages.

Differences between recursive and recursively enumerable languages.

Factor	Recursive / Turing decidable languages)	Recursively enumerable / Turing recognizable languages)
Examples	Context-sensitive languages	RE languages.
States	Halt-Accept, Halt-Reject	Halt-accept, Halt-Reject, Infinite Loop(No halting)
Looping	Finite loops	Possibility of infinite loop
Accept/reject	Accept (Turing machine) = L, Reject (Turing machine) = L, Loop (Turing machine) = φφ, φ = null φ = null	Accept (Turing machine) = LReject (Turing machine) + Loop (Turing machine) = L’

Properties of both recursive and recursively enumerable languages.

We will state theorems which are also properties of both languages.

1. If language L is recursive, its complement L' is also recursive.
   Proof:
   L is a language accepted by a turing machine that halts on all inputs. We construct a turing machine Ts from T as shown below:

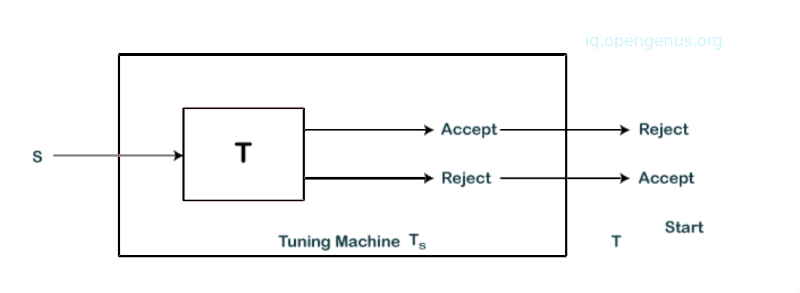
We see that turing machine T given an input string S enters into an accepting state then Ts rejects and halts for string W. Also, if the turing machine T halts without accepting W, Ts enters into an accepting state. Ts accepts strings that are not accepted by T. Therefore, Ts recognizes the complement of L.

2. If the languages L1 and L2 are recursive, their union L1 U L2 is also recursive.
   Proof:
   We have two turing machines T1 and T2 that recognize languages L1 and L2. We construct a turing machine T as shown:

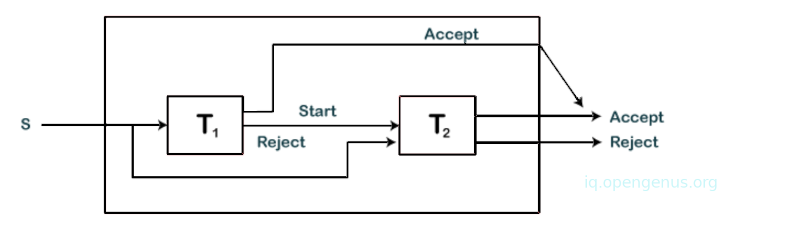
T simulates T1 and T accepts input S is T1 accepts it also. On the other hand, if T1 rejects, T simulates T2 and accepts if T2 accepts.
Both T1 and T2 are algorithms and therefore they will halt at some point. We conclude that T accepts L1 U L2.

3. The union of any two recursively enumerable languages is also a recursively enumerable language.
   Proof: We have two recursively enumerable languages L1 and L2 that are accepted by turing machines T1 and T2. We construct a turing machine T as shown below.

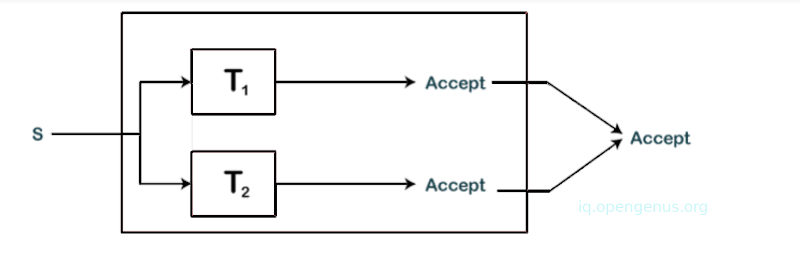
The machine simultaneously simulates T1 and T2 on separate tapes. If either accepts S then machine T also accepts S.

4, We have a language L and its complement L', a recursively enumerable language. Then L will also be a recursive language.
Proof:
We have two turing machines T1 and T2 that recognize languages L and its complement L'. We construct a turing machine T as shown:

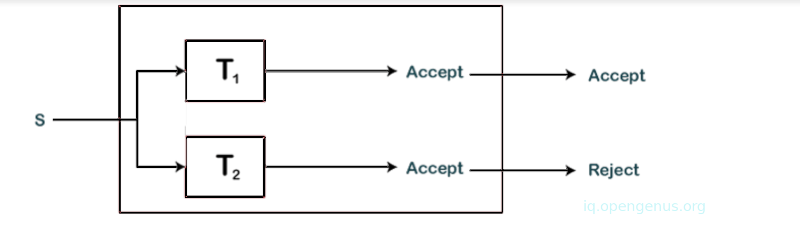
The machine T simulates T1 and T2 parallelly. States of T1 and T2 are components of the state of turing machine T. If T1 accepts S, T accepts S also, if T2 accepts S, T rejects S. This is so since S can either be part of L or part of L' therefore a single machine between T1 and T2 is expected to accept S.
From that, we learn that T will always accept or reject either but never both. Since T is an algorithm that accepts L we say that language L is recursive.

Summary.

We have learned about the properties of recursive and recursively enumerable languages in terms of union, intersection and complements.
A language L as recursive if there exists a turing machine T for it. The turing machine accepts every string in language L and rejects all strings that don't match the alphabet of L

On the other hand, if there is a turing machine T that accepts a language L, the language in which an enumeration procedure exists is referred to as a recursively enumerable language.

With this article at OpenGenus, you must have the complete idea of Recursive and Recursively Enumerable Languages.