Residual Connections in DL

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article at OpenGenus, we will explore the concept of Residual Connections in deep learning.

Table of contents:

Introduction
Mathematical Model
Residual Connections and Model Architectures
Implementation of Residual Connections
Advantages of Residual Connections
Challenges and Considerations
Conclusion

Introduction

Deep neural networks have revolutionized the field of machine learning and have achieved remarkable success in various domains, including computer vision, natural language processing, and speech recognition. However, as networks grow deeper, they often suffer from the vanishing gradient problem, where the gradients propagated through the network diminish, leading to slower convergence and degraded performance. To address this issue, He et al. introduced residual connections, also known as skip connections, as a simple yet effective technique to improve the training and performance of deep neural networks. In this article, we will take a comprehensive look at residual connections, their motivation, implementation, and their impact on deep learning models.

The Motivation for Residual Connections:
Deep neural networks learn hierarchical representations by stacking multiple layers on top of each other. Each layer captures increasingly abstract features of the input data. However, as the network becomes deeper, the gradients flowing backward during training become extremely small, making it difficult for the network to learn effectively. The vanishing gradient problem inhibits the network's ability to propagate useful information throughout the entire network, preventing deep networks from reaching their full potential. Residual connections were introduced to alleviate this problem and enable the training of much deeper networks.
Understanding Residual Connections:
Residual connections work by introducing shortcut connections that allow the gradient to flow directly from one layer to another without any alteration. Unlike traditional feedforward connections, residual connections add the original input (identity mapping) to the output of a subsequent layer. The idea behind this approach is that if the subsequent layer is unable to improve upon the input, the identity mapping will retain the original information, ensuring that it reaches the later layers. This way, the network can learn residual functions, which are the differences between the desired mapping and the input.

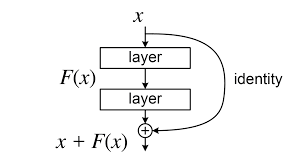
res-conn

Mathematical Model

Let's consider a neural network layer denoted as H(x), where x is the input to the layer. The desired output of the layer is denoted as F(x). The residual connection adds the input x to the output of the layer, resulting in the output of the residual connection as R(x) = x + H(x).

In the context of a deep neural network, the entire network can be represented as a composition of multiple layers, each with its own residual connection. Let's consider a network with L layers. The output of the network can be denoted as Y(x), where x is the input to the network.

To define the mathematical model for the network with residual connections, we can express the output of the network as a recursive equation:

Y(x) = R_L(R_{L-1}(...(R_2(R_1(x))))),

where R_i represents the residual connection at layer i.
Expanding the equation, we have:

Y(x) = x + H_L(x) + H_{L-1}(R_{L-1}(x)) + ... + H_2(R_2(R_1(x))),

where H_i represents the mapping performed by layer i.

The above equation shows how the output of the network is obtained by summing the input x with the mappings performed by each layer, taking into account the residual connections.

The key idea behind the residual connections is that the network learns the residual mapping, which is the difference between the desired output F(x) and the input x. By adding the residual mapping to the input, the network can focus on learning the differences or changes required to obtain the desired output, rather than learning the entire mapping from scratch.

In the training process, the network learns the parameters of each layer, including the weights and biases, to minimize a predefined loss function. The gradients flow through the network during backpropagation, and the residual connections enable the gradients to propagate effectively, addressing the vanishing gradient problem and allowing for the training of deeper networks.

By incorporating the residual connections, the network can learn more efficiently, capture complex relationships, and enable the training of deeper architectures, leading to improved performance in various machine learning tasks.

Residual Connections and Model Architectures

Residual connections have had a significant impact on the development of various model architectures, enhancing their performance and enabling the training of deeper and more expressive networks. Let's explore how residual connections have been integrated into different model architectures.

Residual Neural Networks (ResNets):
Residual connections were first introduced in the context of ResNets, which are deep neural network architectures that consist of residual blocks. A residual block contains multiple stacked convolutional layers, and residual connections are added to each block. By introducing these connections, ResNets overcome the vanishing gradient problem and enable the training of extremely deep networks. This architecture achieved breakthrough results in image classification tasks and won the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC) in 2015.
DenseNet:
DenseNet is another notable architecture that incorporates residual connections. In DenseNet, each layer is connected to every other layer in a feed-forward manner. DenseNet blocks are composed of dense layers, where each layer receives direct inputs from all preceding layers. This design allows information to flow directly from early layers to later layers through short connections, promoting feature reuse and enabling better gradient flow. The skip connections in DenseNet can be considered as a form of residual connection.
Highway Networks:
Highway Networks are architectures that utilize residual connections to control the flow of information within the network. In Highway Networks, the residual connections are used to model adaptive gating mechanisms that determine how much of the input should be passed through and how much should be transformed. These gates are learned during training, allowing the network to decide when to skip or transform the input at each layer. By leveraging the residual connections and gating mechanisms, Highway Networks can effectively capture long-range dependencies and improve the flow of gradients.
Transformer Models:
Residual connections have also been applied to transformer models, which have revolutionized natural language processing tasks. In the original Transformer architecture, residual connections are introduced in the form of "multi-head attention" and "feed-forward" sub-layers. Within each sub-layer, residual connections allow the information to bypass the attention or feed-forward layers, facilitating the flow of gradients and enabling effective training of deep transformer models.
Other Architectures:
Residual connections have been adopted and customized in various other model architectures. These include variants of recurrent neural networks (RNNs), such as LSTM (Long Short-Term Memory) networks and GRU (Gated Recurrent Unit) networks, where residual connections can be applied to the recurrent layers to address the vanishing gradient problem and improve long-term dependency modeling. Additionally, residual connections have been explored in areas like object detection, semantic segmentation, and generative models, among others, to enhance performance and stability.

By integrating residual connections into these model architectures, researchers and practitioners have achieved significant advancements in performance, training stability, and scalability. Residual connections enable the development of deeper and more expressive networks, allowing models to capture complex patterns and improve generalization capabilities. Overall, the widespread adoption of residual connections in various model architectures highlights their effectiveness in enhancing deep learning models and their contribution to advancing the field of machine learning.

Implementation of Residual Connections

Implementing residual connections involves adding shortcut connections that bypass certain layers and allow the gradient to flow directly from one layer to another without alteration. This can be done in various neural network architectures, including convolutional neural networks (CNNs) and residual neural networks (ResNets). Let's explore the implementation of residual connections in more detail.

Residual Connections in Convolutional Neural Networks (CNNs):

In CNNs, residual connections are typically introduced by adding the input feature maps directly to the output feature maps of a convolutional layer. This is commonly referred to as a "skip connection" because it allows the information to skip a few layers and directly reach subsequent layers.
Let's consider a basic block in a CNN architecture, consisting of two convolutional layers. The input to the block is denoted as x, and the output of the block is denoted as F(x), where F represents the mapping performed by the convolutional layers. To introduce a residual connection, we modify the output of the block as follows:

output = x + F(x)

Here, the input x is added element-wise to the output of the convolutional layers. This addition operation combines the original input with the features extracted by the convolutional layers, allowing the gradient to flow directly through the addition operation during backpropagation.

Residual Connections in Residual Neural Networks (ResNets):

Residual connections are a central component of ResNets, a specific type of deep neural network architecture. In ResNets, residual connections are added to each residual block, which typically consists of multiple convolutional layers. The addition of residual connections enables the training of very deep networks with hundreds or even thousands of layers.
Let's take a closer look at the implementation of residual connections within a residual block in a ResNet. Suppose we have an input x and a desired mapping H(x) that the block is supposed to learn. The residual block can be defined as follows:

output = x + H(x)

Here, H(x) represents the mapping performed by the convolutional layers within the block. Similar to the skip connection in CNNs, the input x is added to the output of the block, allowing the network to learn the residual mapping H(x). By learning the residual mapping, the network can focus on capturing the differences between the desired mapping H(x) and the input x, rather than learning the entire mapping from scratch.

Residual connections are typically introduced after each set of convolutional layers in a residual block. This enables the gradients to bypass the block and directly propagate to subsequent layers, facilitating the flow of gradients throughout the network.

Placement and Design Considerations:

The placement and design of residual connections depend on the specific architecture and task at hand. In deeper architectures, it is common to have multiple residual blocks stacked together. In such cases, it is crucial to ensure that the dimensions of the input and the output of the block match so that they can be added together. This can be achieved through techniques such as adjusting the number of channels or using 1x1 convolutions for dimensionality matching.
Additionally, the design of residual connections can be customized based on the specific requirements of the task. For instance, in some cases, it may be beneficial to include additional operations, such as batch normalization or activation functions, within the residual connections to further enhance the performance of the network.

Advantages of Residual Connections

Improved Gradient Flow: The main advantage of residual connections is that they facilitate the flow of gradients during backpropagation. By providing shortcut paths for the gradients, residual connections mitigate the vanishing gradient problem, allowing the network to learn effectively even with very deep architectures.
Easy Optimization: Residual connections simplify the optimization process by making it easier for the network to approximate the identity mapping. The network has the flexibility to choose whether to use the identity mapping or learn a different mapping based on the input.
Deeper Networks: Residual connections have enabled the training of extremely deep neural networks that were previously challenging to optimize. Deep networks with hundreds or even thousands of layers can now be trained successfully, leading to improved performance and accuracy.

Challenges and Considerations

While residual connections have proven to be highly effective in improving deep neural networks, there are a few considerations and challenges associated with their usage. One key consideration is the introduction of additional parameters and computational overhead due to the presence of skip connections. Although the benefits usually outweigh the added complexity, careful design and optimization are necessary to strike a balance between model expressiveness and efficiency. Additionally, the optimal placement and design of residual connections may vary depending on the specific task and dataset, requiring empirical exploration.

Conclusion

Residual connections have emerged as a fundamental technique in the field of deep learning, addressing the vanishing gradient problem and enabling the training of significantly deeper neural networks. By providing shortcut connections, residual connections facilitate the flow of gradients, leading to improved optimization and enhanced model performance. With their widespread adoption across various architectures, residual connections have played a pivotal role in pushing the boundaries of deep learning and achieving state-of-the-art results in numerous tasks. As research in deep learning continues to evolve, residual connections remain a valuable tool in the quest for more powerful and efficient neural networks.