Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
The problem is to determine whether a given set can be partitioned into two subsets such that the sum of elements in both subsets is same.
The time complexity of solving this using Dynamic Programming takes O(N x SUM) time where N is the number of elements and SUM is the sum of elements in either of the subsets.
If we solve this problem using recursive approach then time complexity would be exponential but we can use dynamic programming approach to reduce this complexity.In dynamic programming approach we break down the problem into smaller sub-problems and use the result of each to build to our solution.In this article,first of all we will explore the recursive approach and then go into dynamic programming approach to solve this efficiently.
Example
arr[] = {2,6,3}
Output : False
The array can't be partitioned into equal sum sets
arr[] = {2,2,3,3}
Output : True
Array can be partitioned as {2,3} and {2,3}
Before moving further let's have some knowledge about OR operator.
OR Operator
It is a logical operator.It is denoted by "||" symbol.Let A and B be two operands on which we are applying OR operator.
(A||B) = true,if any of the operands either A or B is non-zero.
So,we can say (A||B) will be equal to false if and only if both A and B is zero.
Property:
- A=1,B=0 => (A||B) = 1
- A=0,B=0 => (A||B) = 0
- A=0,B=1 => (A||B) = 1
- A=1,B=1 => (A||B) = 1
Method
To solve this problem,three major steps are :
- Calculate the sum of the given array.
- If the sum is odd then we can't partition the array into two subsets having equal sum.In this case,return False.
- If the sum is even then we will try to find a subset having sum of array elements equal to (sum/2).If such subset exists then return True.
The first and second step is very easy.
Third step can be solved using recursion as well as dynamic programming.We will create a function partition which handles first and second step.
For third step we will create another function isSubsetsum which returns true if there exists a subset having sum equal to (sum/2) else return false.Now our main target is to implement isSubsetsum function.For obtaining a subset from a given set having sum equal to (sum/2),for each element of the given set we will consider two possibilities whether to include that element in these subset or not.If the element is greater than the required sum then we will not include that element.But if that is not the case then we have to consider both possibilities whether to include or not.
Recursive Approach
Pseudocode:
As explained earlier calculate the sum of the given array and if the sum is odd then just return false but if the sum is even then call isSubsetsum(),if this function returns true then return true else return false.Let's understand isSubsetsum() function.
Let isSubsetsum(arr,n,sum) be the function that returns true if there is a subset of arr[0..n-1] with sum equal to (sum/2).
The isSubsetsum problem is divided into two subproblems
1. isSubsetsum(arr,n-1,sum) without considering last element.
2. isSubsetsum(arr,n-1,sum-arr[n-1]) considering last element.
If any of the above subproblems return true,then return true else return false.
Implementation:
#include<bits/stdc++.h>
using namespace std;
//If there exits a subset in the given array having sum equal to given sum then this function returns true.
bool isSubsetsum(int arr[],int n,int sum){
//Base Cases
if(sum==0){
return true;
}
if(n==0 & sum!=0){
return false;
}
//If last element is greater than sum,then ignore it.
if(arr[n-1]>sum){
return isSubsetsum(arr,n-1,sum);
}
//If last element is not greater than sum then we are considering both the possibilities i.e. either include the last element or exclude it.If any possibility returns true then this function returns true.
return isSubsetsum(arr,n-1,sum) || isSubsetsum(arr,n-1,sum-arr[n-1]);
}
//This function returns true if arr[] can be partitioned into two subsets of equal sum.
bool partition(int arr[],int n){
int sum=0;
//calculate sum of the elements in array.
for(int i=0;i<n;i++){
sum+=arr[i];
}
//If sum is odd,there cannot be two subsets with equal sum.
if(sum%2!=0){
return false;
}
//If sum is even,then call function isSubsetsum()
return isSubsetsum(arr,n,sum/2);
}
int main(){
int arr[] = {2,6,3};
int n=3;
if(partition(arr,n)){
cout<<"True"<<endl;
}else{
cout<<"False"<<endl;
}
return 0;
}
Output:False
- Time Complexity : O(2^n)
Dynamic Programming Approach
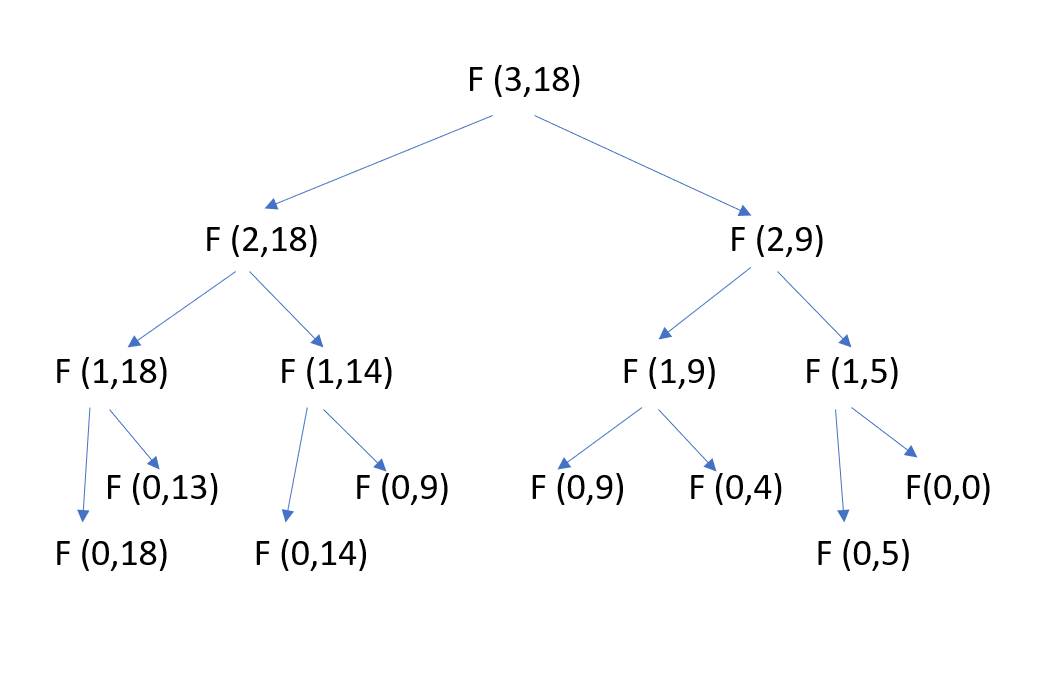
The recursive approach is computing the same subproblems again and again.That's why its complexity is high.Let's see the recursion tree for arr[] = {5,4,9}.In this example,since the sum is even so isSubsetsum() function is being called.
In recursion tree F(i,j) represents function isSubsetsum where i represents size of the array and j represents sum.
The function F(0,9) is called two times.For large values of n and sum, there will be many subproblems which are being called again and again.The re-computation of subproblems can be avoided by applying dynamic programming techniques.
Pseudocode:
- Calculate the sum of given array.If sum is odd then returns false else call function isSubsetsum().
- Implement isSubsetsum().If this function returns true then return true else return false.
Let isSubsetsum(arr,n,sum) be the function that returns true if there is a subset of arr[0..n-1] with sum equal to (sum/2).To implement this function in bottom up manner we will create a 2d-array dp[][] whose row represents the sum and column represents the size of an array.Value at dp[i][j] will be true if there exists a subset of size less than or equal to j and sum equal to i.
dp[i][j] = true if a subset of size less than or equal to j having sum equal to i is found,otherwise false.
Base Case:
dp[0][i]=true
dp[i][0]=false; if i < Sum
Recursive relation:
If last element is not greater than sum then we are considering both the possibilities i.e. either include the last element or exclude it.If any possibility returns true then store true in the array.
for(int i=1;i<=sum;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i][j-1]; //Excluding last element
if(i>=arr[j-1]){
dp[i][j]=(dp[i][j]||dp[i-arr[j-1]][j-1]);
Answer is dp[sum][n]
Let's understand this with an example:
arr[] = {3,4,7}
n = 3
Now,row of dp[][] array ranges from 0 to 7 and column ranges from 0 to 3.Here, dp[3][1]=true because there exist a subset of size 1 having sum equal to 3.Also dp[3][2]=true because there exist a subset of size less than 2 having sum equal to 3.Similarly,we can fill the entire dp[][] array and if dp[7][3]=true then isSubsetsum returns true.
Implementation
#include<bits/stdc++.h>
using namespace std;
//If there exits a subset in the given array having sum equal to given sum then this function returns true.
bool isSubsetsum(int arr[],int n,int sum){
bool dp[sum+1][n+1];
//If sum is 0,then store true.
for(int i=0;i<=n;i++){
dp[0][i]=true;
}
//If n=0 but sum!=0 then store false.
for(int i=1;i<=sum;i++){
dp[i][0]=false;
}
//Filling the dp array.
for(int i=1;i<=sum;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i][j-1]; //Excluding last element
if(i>=arr[j-1]){
dp[i][j]=(dp[i][j]||dp[i-arr[j-1]][j-1]); //If last element is not greater than sum then we are considering both the possibilities i.e. either include the last element or exclude it.If any possibility returns true then store true in the array.
}
}
}
return dp[sum][n];
}
//This function returns true if arr[] can be partitioned in two subsets of equal sum.
bool partition(int arr[],int n){
int sum=0;
//calculate sum of the elements in array.
for(int i=0;i<n;i++){
sum+=arr[i];
}
//If sum is odd,there cannot be two subsets with equal sum.
if(sum%2!=0){
return false;
}
//If sum is even,then call function isSubsetsum()
return isSubsetsum(arr,n,sum/2);
}
int main(){
int arr[] = {5,4,9};
int n=3;
if(partition(arr,n)){
cout<<"True"<<endl;
}else{
cout<<"False"<<endl;
}
return 0;
}
Output:True
Step by step Explanation
dp[i][j]=(dp[i][j]||dp[i-arr[j-1]][j-1])....-> equation-1
Before this step, we are storing dp[i][j]=dp[i][j-1] this is basically ensuring that if there exist a subset having sum i but excluding the element at (j-1)th index then store true at dp[i][j] and if not then store false.
After this step what we are achieving in equation-1 is that if dp[i][j]=false but there exist a subset having sum (i-arr[j-1]) and this sum exists without the element at (j-1)th index then store true i.e. in any case if there exist a subset having sum i but excluding the element at (j-1)th index or there exist a subset having sum (i-arr[j-1]) and this sum exists without the element at (j-1)th index store true at dp[i][j].
In the situation when neither of the condition is true then store false at dp[i][j].
Example
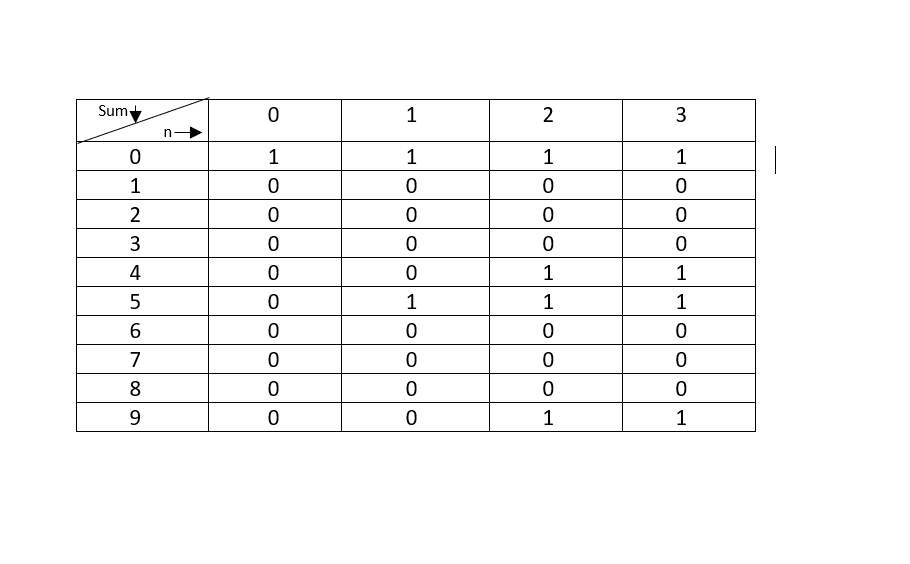
arr[] = {5,4,9}
Output : True
sum=5+4+9=18
since,sum is even so we will call isSubsetsum() function.
dp[][] array obtained is :
Since dp[9][3]=1 ,therefore returns true.
Complexity
- Time Complexity : O(n.sum)
- Space Complexity : O(n.sum)
Question
- Can we partition the array arr[]={3,6,5,3,7,9} into two subsets of equal sum?
- Yes
- No