Algorithms for Calculating Day of Week

There are several algorithms present which can be used for the determination of day of the week. These mathematical algorithms makes calculation of the day quick and fun. This article will be covering related algorithms.

Let's first cover few basic definitions:

• Julian Calender
• Georgian Calender

Some of the Algorithms for Calculating Day of Week are:

• Tomohiko Sakamoto Algorithm
• Gausses Algorithm
• Wang's Algorithm

Julian Calender

This calender has two years: Normal Year with 365 days and Leap year with 366 days
This calender observes three consecutive normal years followed by a leap year.

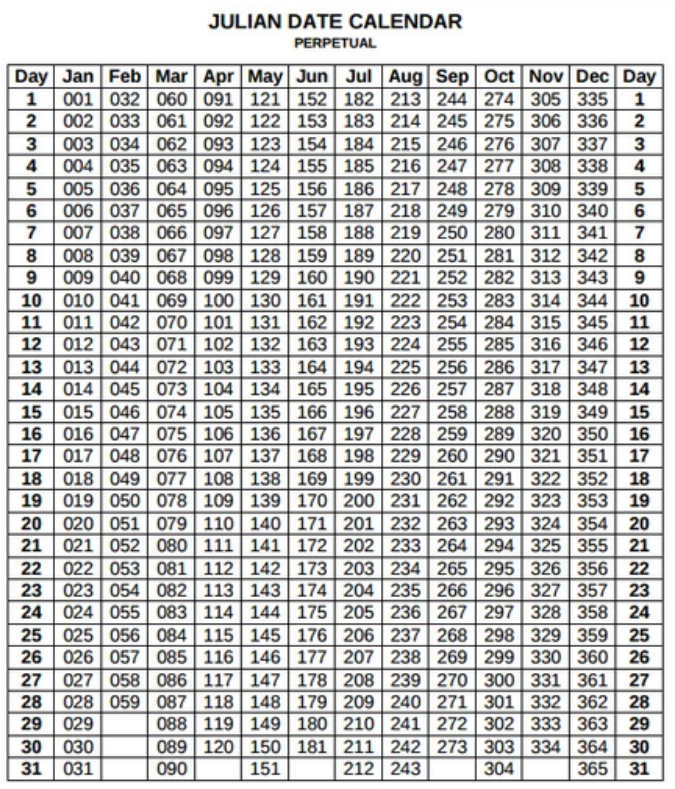
Georgian Calender

This calender is an improved version of Georgian Calender. It should be noted that Georgian Calender is far more popular than Julian Calender.

Every year divisible by 4 is a leap year. Those year which are divisible by 100 are not but those which are divisible by 400 are.

The main difference between Julian calender and Georgian Calender are leap year rules.

Mathematical Algorithms

The main aim of these algorithms is to correctly synchronize the days of week according to months and year so that accurate day can be calculated. Each of the algorithm undertakes different approaches.

Tomohiko Sakamoto Algorithm

This method uses Georgian Calender. It is one of the most powerful and less well known ways of the calculation.

int dow(int y, int m, int d){
static int t[] = {0, 3, 2, 5, 0, 3, 5, 1, 4, 6, 2, 4};
y -= m < 3;
return (y + y/4 - y/100 + y/400 + t[m-1] + d) % 7;
}

This aims in finding the number of days till now %7 by assuming the first day to be Monday.
y counts number of odd days till previous year assuming it not be a leap year. Here it is to be noted that every year has an odd day except for leap years.
The expression (y/4 - y/100 + y/400) looks after the odd days due to leap year.
Array t[] depicts number of days occurred in that year till previous month % 7. t[i] are number of odd days in previous month.
Days in current month is d.

Now using the formula (y + y/4 - y/100 + y/400 + t[m-1] + d) % 7 gives the day for the particular date.

• Here is the link to a more detailed article about Tomohiko Sakamoto Algorithm

Gausses Algorithm

Using the Georgian Calender in this weekdays are numbered from 0 to 6. Starting with Sunday the weekday of 1 January for year number A is given by:

R (1+5R (A - 1, 4) + 4R (A - 1, 100)+ 6R (A - 1, 400),7)
Here R(y,m) represents the reminder obtained by division of y by m.
A is Y+100C

This can be used for Julian Calender by the following formula:

R (6 +5R (A-1, 4) +3(A-1), 7)
R(y,m) represents remainder obtained by division of y by m.
A is Y+100c

Wang's Algorithm

This method uses null-days for months, days, and years to be converted to integers. Then simple arithmetic operations can provide with the day of week.
For Georgian Calender the formula is as follows:

It should be noted that if m is 1 or 2 and it's a leap year then the formula should be subtracted by 1.

Months(m) are January {1} until December{12}
Days(d) are 1 until 31
Weekdays(w) are Sunday{0} until Saturday{6}

w = (d - d^(m) + y^ - y* + [y^/4 - y*/2] - 2( c mod 4)) mod 7
y^ and y* is the last and second last digit of the year respectively.
c is the first 2 digits of the year
d^(m) represents null day

For Julian Calender :

w = (d - d^(m) + y^ -y1 + [y^/4 - y*/2] - c) mod 7
The representation of variables in formula is same as above.

These covered algorithms and their formulas can be used to find the day of the week in either Julian or Georgian calender. Implementation can be done by using these formulas in languages (like C, C++, Java) during coding.