
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 10 minutes
Sparse table is a data structure which pre-process the information to answer static Range Queries. In this article, first we will understand what are sparse table with an example of Range Minimum Query. Then we will implement it in python and lastly, we will compare sparse tables with other algorithms to get an overall idea about it's optimality. Let's get started!
Lets start by considering the array below,
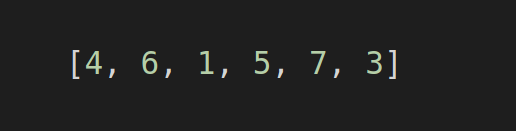
Now, lets say that I want to know the minimum value from the sub-array of this array. One can start with a brute force method but it would be off the charts if efficient solution is what one seeks. How about we try it with sparse table. To set up an static sparse table query, there are two major steps. First, to create a sparse table and second, to set up the query mechanism.
Creating a sparse table
We will be using the array from above to create a sparse table for Range Minimum Query (Static). First step would be create blank 2-D table of size, (array length) x (log(array length)). One might ask about the log, then I would say wait for now and go along with the tutorial, you will know the reason soon enough.
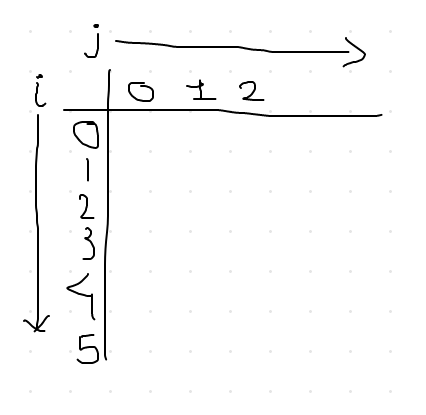
So, I have created a blank table where i represents the array length and j the log of it. If you get the log of the array value not in integers then take the closest greater integer value from that value. For example, log of 6 base 2 is somewhere between 2 and 3, so you should take the greater integer that is 3. Similarly, you can notice that there are three numbers on j axis.
Starting with j=0 and i=0, find the index i in the array, whose value is 4, and find the value of 2^{j}, which is 1. This means that starting from index i we need to consider the sub-array of length 1 or it should contain 1 element, which is 2^{j}. Calculating this for our example, the sub-array would only contain {4} because the limit of 1 element is reached. Now in this sub-array, which value is the lowest? Of course, it is 4 right? We will put the index of 4 which is 0 in our table. Just like below.
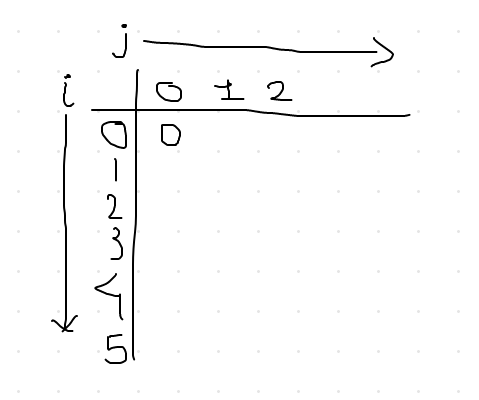
Now repeating the same for all the possible value of i, fixing j=0 our table should look like this.
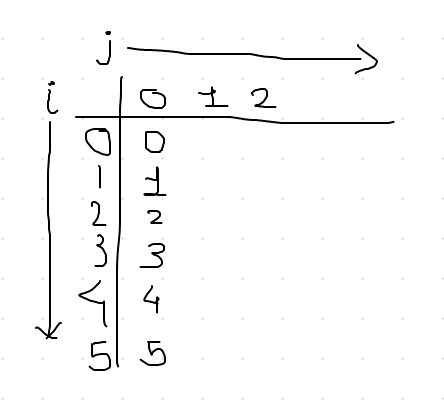
Now our increases to j=1 and i=0. For this combination our sub-array would now contain two elements starting from index i (which is 0), {4, 6}. Well 4 is the smaller so we will put 0 in the table. Second step would be to increase i and it's value will be i=1. Our array would be {6,1}, from which 1 is the smallest value and it's index is 2. So, 2 will go to our table for i=1 and j=1. Our table would look like below at this point.
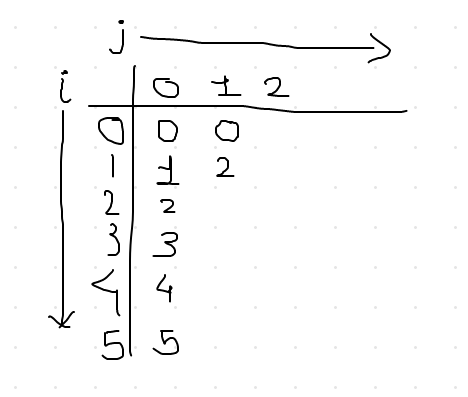
If you repeat the steps for every remaining combination of i till i=4 with j being at j=1, our table would just look like,
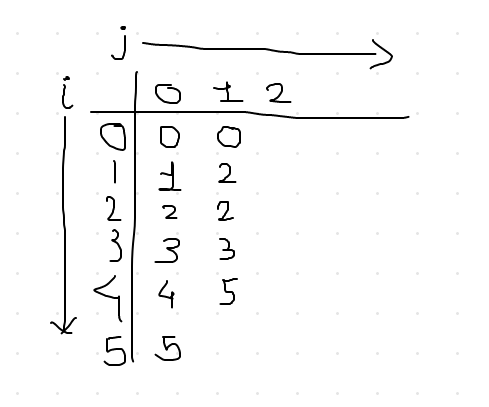
Now, we cannot go further because only one element left in the array and to move forward we need exactly 2. When you hit this kind of situation, like 2^{j} < (number of elements left), skip every possible value of i for that value of j. Increment the j, which will be j=2, and start from i=0. After you do this calculation for remaining combination, table should look like this,
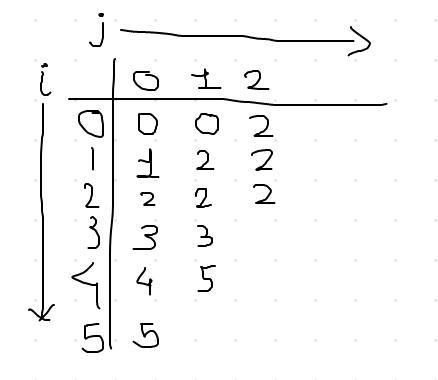
Congrats! You have successfully made a sparse table for static range minimum query. Next step would be to understand how to decode the query so you can extract the range minimum.
Decoding the query
Considering the sparse table in the previous image, we will take some random cases to understand the decoding process. such as, find minimum value between (3, 5), (0, 5) and (0, 3).
Starting with (3,5), so this range contains this elements, {5,7,3}. First we will find out the length of this array, which is 3 and lets call it as 'l'. Then we will calculate log(3), or the log(length of the query), rounding to its minimum smallest integer if not and called it k. For our example, k will be 1. From this information, first_element=3 and k=1, we will look for index 3 in the i axis of the table and index 1 on j axis. The value at (i=3,j=1) is 3 which is the index of the array whose value is 5. Now we will subtract 2^{k} from the length of the query, which will be 3-2 = 1. This means 1 elements is still left in the query range. For that, we have to add this remaining value to original first_element value, 3+1=4. Now we will find for i=4 and and j=1 from the table for which the answer is index 5 whose value is 3. We had to do two sub queries, (3,4) and (4,5), and their answer is 5 and 3, respectively. The answer for our original query, (3,5), will be the minimum of these two value which is 3.
Try on remaining examples, let me know if you have any trouble solving them.
Python implementation of sparse table
Below is the python implementation of the sparse table data type for the range minimum query. Hope you find it useful.
import math
def construct_sparse_table(arr):
n = len(arr)
sparse_table = [[-1 for i in range(n)]
for j in range(int(math.log(n, 2))+1)]
for j in range(int(math.log(n, 2))+1):
for i in range(n):
min_index = i
if(i+(2**j)-1 < n):
for x in range(i, i+(2**j)-1):
if(given_array[x] < given_array[min_index]):
min_index = x
sparse_table[j][i] = min_index
return sparse_table
def query(arr, sparse_table, query_range):
length_of_array = len(arr)
min_elements = []
while length_of_array > 0:
k = int(math.log(len(arr), 2))
min_elements.append(arr[sparse_table[k][query_range[0]]])
length_of_array = length_of_array - (2**k)
return min(min_elements)
if __name__ == '__main__':
given_array = [4, 6, 1, 5, 7, 3]
sparse_table = construct_sparse_table(given_array)
query_list = [[3, 5], [0, 5], [0, 3]]
for x in query_list:
print(query(given_array, sparse_table, x))
Comparison
Of course, there are many ways to solve this problem but I bet this is not the worst so far. Below is the comparison table for the info.
| Algorithm | pre-processing | query |
|---|---|---|
| Brute force | O(1) | O(N) |
| Dynamic Programming | O(N^2) | O(1) |
| segmentation tree | O(N) | O(logN) |
| Sparse Table | O(NlogN) | O(1) |
I hope you enjoyed this article. Happy coding!
