You are given a string and a pattern as the input, the pattern contains some wildcard characters such as '*' & '?'. Here '?' can match to any single character in input string and * can match to any number of characters including zero characters. We have to report the answer in form of "yes" if the pattern matches the string else report and "no" if it does not matches.

We will be using a Dynamic Programming approach with the time complexity of O(m * n), here m and n represent length of string and pattern respectively. For example:

Input: string : xyxzzxy,pattern : x**y
Output: Yes

Input: string : yzzzxy, pattern : x*x
Output: No

Input:string : xyyzxy, pattern : x?yzxy
Output: Yes

Input format

Enter the string : yzxyxy
Enter the pattern : y**y

Output format

Yes

Method of Implementation

We will solve the problem by applying the following approach:
Step 1: If the current character of the pattern is * and if it matches with the present character of the string we can just move one step forward in string.
Step 2: If the * does not matches then we can just ignore it and move forward in the pattern by one step.
Step 3: If the current character of the pattern is '?' then we move forward in both pattern and string.
Step 4: If the current character of the pattern is not a wildcard character then it should positively match with the current character of the string.
Step 5: If we have reached the end of both string and pattern then we return true.
Step 6: If still string is left to be traversed and we have already reached the end of pattern then return false.
Step 7: If we have reached the end of string but the pattern is still left to be traversed then we will return true only if the rest of the characters in the pattern are only *.

Pseudocode

Step 1: Create a boolean 2-D matrix mat[m+1][n+1] where m is the length of the string and n is the length of the pattern.
Step 2: Initialize mat[0][0]=1(because empty string and empty pattern always match.
Step 3: Initialize mat[i][0]=0, because pattern will be empty.
Step 4: Update the value of mat[0][i]=mat[0][i-1] if the current pat[i-1] = *.
Step 5: Now start the comparison. If the current character of pattern is * then the value of mat[i][j]=mat[i-1][j]||mat[i][j-1].
Step 6: If the current character of pattern is '?', then both the current characters of pattern and string should match, therefore mat[i][j]= mat[i-1][j-1].
Step 7: If the current character of pattern is not wildcard character and if both the characters of pattern and string matches then mat[i][j]=mat[i-1][j-1]. Else if they don't match mat[i][j]=0.

Implementation

#include<bits/stdc++.h>
using namespace std;

bool wildcard(string str, string pat)
{
	int i,j;
	int m=str.length();
	int n = pat.length();
	
	bool mat[m+1][n+1];
	
	//Initialise whole matrix to false
	for(i=0;i<=m;i++)
	{
		for(j=0;j<=n;j++)
		mat[i][j]=false;
	}
	
	//because empty string and empty pattern always match
	mat[0][0]=true;
	
	//if the string is null
	for(i=1;i<=n;i++)
	{
		if(pat[i-1]=='*')
		mat[0][i]=mat[0][i-1];
	}
	
	for(i=1;i<=m;i++)
	{
		for(j=1;j<=n;j++)
		{
			//if current character of pattern is *
			if (pat[j - 1] == '*') 
            mat[i][j] = mat[i][j - 1] || mat[i - 1][j];
                          
		    //if the character is ? then consider them to match   
            else if (pat[j - 1] == '?') 
            mat[i][j] = mat[i - 1][j - 1]; 
             
            else if(str[i - 1] == pat[j - 1])
            mat[i][j] = mat[i - 1][j - 1]; 
            
            //if it does not matches any condition
            else mat[i][j] = false; 
		} 
	}
	return mat[m][n];
}

int main()
{
	string str, pat;
	//Enter the string
	cout<<"Enter your string :"<<endl;
	cin>>str;
	//Enter the pattern to be checked
	cout<<"Enter your pattern :"<<endl;
	cin>>pat;
	bool result = wildcard(str, pat);
	if(result==1)
	cout<<"Yes";
	else
	cout<<"No";
}

Complexity Analysis:

Time complexity: O(m x n)
Space complexity (Auxillary Space):O(m x n)

Explaination with example:

String: xyzzzyx
Pattern: x***x

After initialising the matrix mat[8][6] with all the required values when either or both string and pattern are null, we start filling the matrix in bottom-up manner,
mat[8][6] looks like:

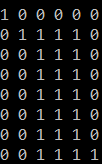
We get the above by matrix by comparing characters of string and pattern. If the character of pattern is * we take the boolean OR of the element just above the cell and the element just left of the cell.
Whereas if the element is ? then we copy the value of the closest left diagonal.
Else we update the value as false.

Applications of Wildcard Pattern Matching

The above algorithm can be used that if the current string matches with pattern which we have and accordingly result may be generated.