Introduction to 2-3 Trees

A 2-3 Tree is a tree data structure where every node with children has either two children and one data element or three children and two data elements. A node with 2 children is called a 2-NODE and a node with 3 children is called a 3-NODE. A 4-NODE, with three data elements, may be temporarily created during manipulation of the tree but is never persistently stored in the tree.

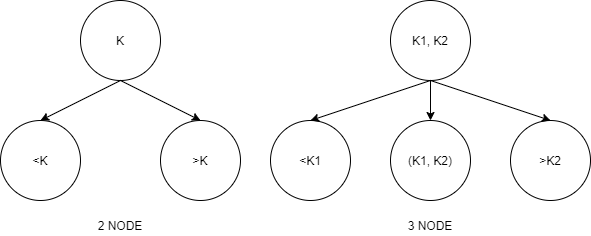
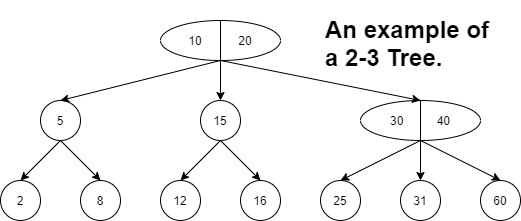
Nodes on the outside of the tree i.e. the leaves have no children and have either one or two data elements. All its leaves must be on the same level so that a 2-3 tree is always height balanced. A 2-3 tree is a special case of a B-Tree of order 3. Below is an example of a 2-3 tree.

Properties of 2-3 Trees

A 2-3 tree follows the below mentioned properties.

1. Every internal node in the tree is a 2-node or a 3-node i.e it has either one value or two values.
2. A node with one value is either a leaf node or has exactly two children. Values in left sub tree < value in node < values in right sub tree.
3. A node with two values is either a leaf node or has exactly 3 children. It cannot have 2 children. Values in left sub tree < first value in node < values in middle sub tree < second value in node < value in right sub tree.
4. All leaf nodes are at the same level.

You can notice that the previous example given satisfies all the above mentioned properties.It is important to note from the above properties that all data in a 2-3 tree is stored in a sorted manner which makes search operations fast and effective.

Operations on a 2-3 Tree

A 2-3 tree supports the three basic operations i.e. searching, inserting and deleting an element.

Searching for an element

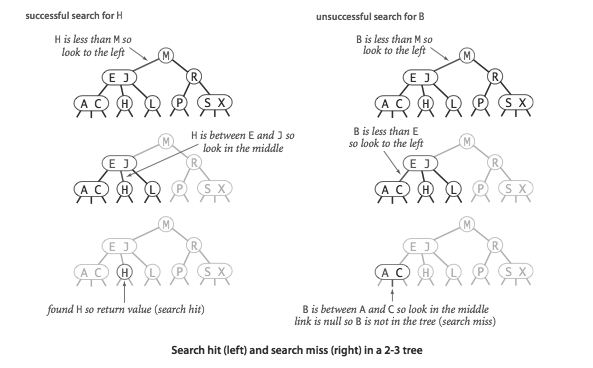
Searching for an element in a 2-3 tree is very similar as searching for an item in a binary search tree. Since the tree is sorted, the search function will be directed to the correct subtree and eventually to the correct node which contains the element.

Let d be the data element we want to search for in the 2-3 tree T. The base cases are as follows:

• If the tree T is empty, then d is not in the tree and we return FALSE.
• If the current node contains value which is equal to d, we return TRUE.
• If we reach the root node and it does not contain d, we return FALSE.

The recursive cases for a 3-Node are as follows:

• If d is less than the left value of the current node, we now consider T to be the left subtree of the current node.
• Else if d is greater than left value and less than right value of current node, we consider T to be the middle subtree of the current node.
• Else if d is greater than the right value of current node, we consider T to be the right subtree of the current node.

The recursive cases for a 2-Node is the same as a binary search tree and is as follows:

• If d is less than the value at the current node we consider T to be the left subtree of the current node.
• If d is greater than the value at the current node we consider T to be the right subtree of the current node.

An example of the search operation

The function to implement the search operation.

//This is a function to check if a 2-3 tree contains a key.
bool contains(t key) {
    //Base case 1
	if(size() == 0) return false;//If size is zero, then it cannot have the key.
	node *search = root;
	while(search) {
        //Base case 2
		if(search->contains(key)) {
			return true;
		}
		if(*search->firstkey > key) {
			search = search->less;
		}else if(*search->firstkey <= key && search->is2node()) {
			search = search->btwn;
		}else {
			if(*search->secondkey > key) {
				search = search->btwn;
			}else {
				search = search->great;
			}
		}	
	}
    //Base case 3
	return false;
}

Inserting an element

The insert operation takes care of the balanced property of a 2-3 tree. The insertion algorithm into a two-three tree is quite different from the insertion algorithm for a binary search tree. In a two-three tree, the algorithm will be as follows:

1. If the tree is empty, create a node and put value into the node.
2. Otherwise find the leaf node where the value belongs.
3. If the leaf node has only one value, put the new value into the node.
4. If the leaf node has more than two values, split the node and promote the median of the three values to parent.
5. If the parent then has three values, continue to split and promote, forming a new root node if necessary.

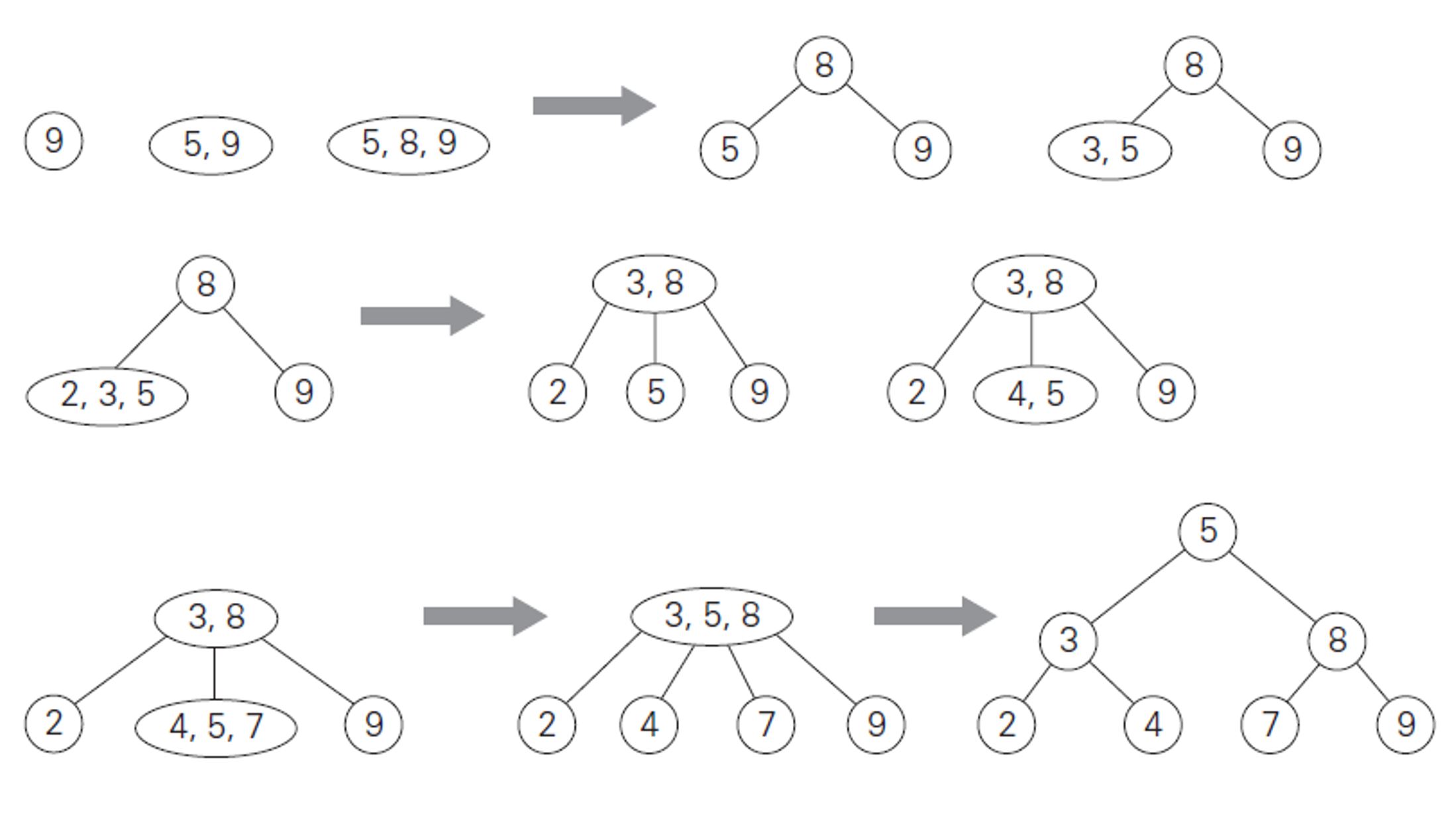
The below example could aid your understanding of the insert algorithm. Let us insert 9, 5, 8, 3, 2, 4, 7 starting from an empty tree.

The function to implement the insert operation.

//A function to implement the insert operation
void insert(node *candidate, t *key) { //Here key is the element to be inserted in the candidate
	if(candidate == nullptr) {
		root = new node(key);
		return;
	}
	if(candidate->isleaf()) {
		candidate->store(key);
	}else {
		if(*candidate->firstkey > *key) {
			insert(candidate->less, key); //Insert to left subtree.
		}else if(*candidate->firstkey <= *key && candidate->is2node()) {
			insert(candidate->btwn, key); //Insert to mid subtree.
		}else {
			if(*candidate->secondkey > *key) {
				insert(candidate->btwn, key); //Insert to mid subtree.
			}else {
				insert(candidate->great, key); //Insert to right subtree.
			}
		}
	}
	split(candidate); //This function is to balance the tree incase of an overflow.	
}

Deleting an element

Deleting a data element d is similar to inserting. There is a special case when T is just a single node containing d. In this case, the tree is made empty. In other cases, the parent of the node to be deleted is found, then the tree is fixed up (if necessary) so that it is still a 2-3 tree. Once the parent of the node n to be deleted is found, there are two cases depending on how many children n has:

If n has 3 children

• Remove the child with value d, then fix the left value, middle value and n's ancestors' left value and middle value if necessary.

If n has 2 children

• If n is the root of the tree, then remove the node containing d. Replace the root node with the other child.
• If n has a left or a right sibling with 3 kids, then:

1. remove the node containing d.
2. use one of the sibling's children.
3. Fix left value, middle value of n and n's siblings and ancestors as needed.

• If n's sibling(s) have only 2 children, then:

1. remove the node containing d
2. make n's remaining child a child of n's sibling
3. fix left value and middle value fields of n's sibling as needed
4. remove n as a child of its parent, using essentially the same two cases (depending on how many children n's parent has) as those just discussed.

An example of the delete operation

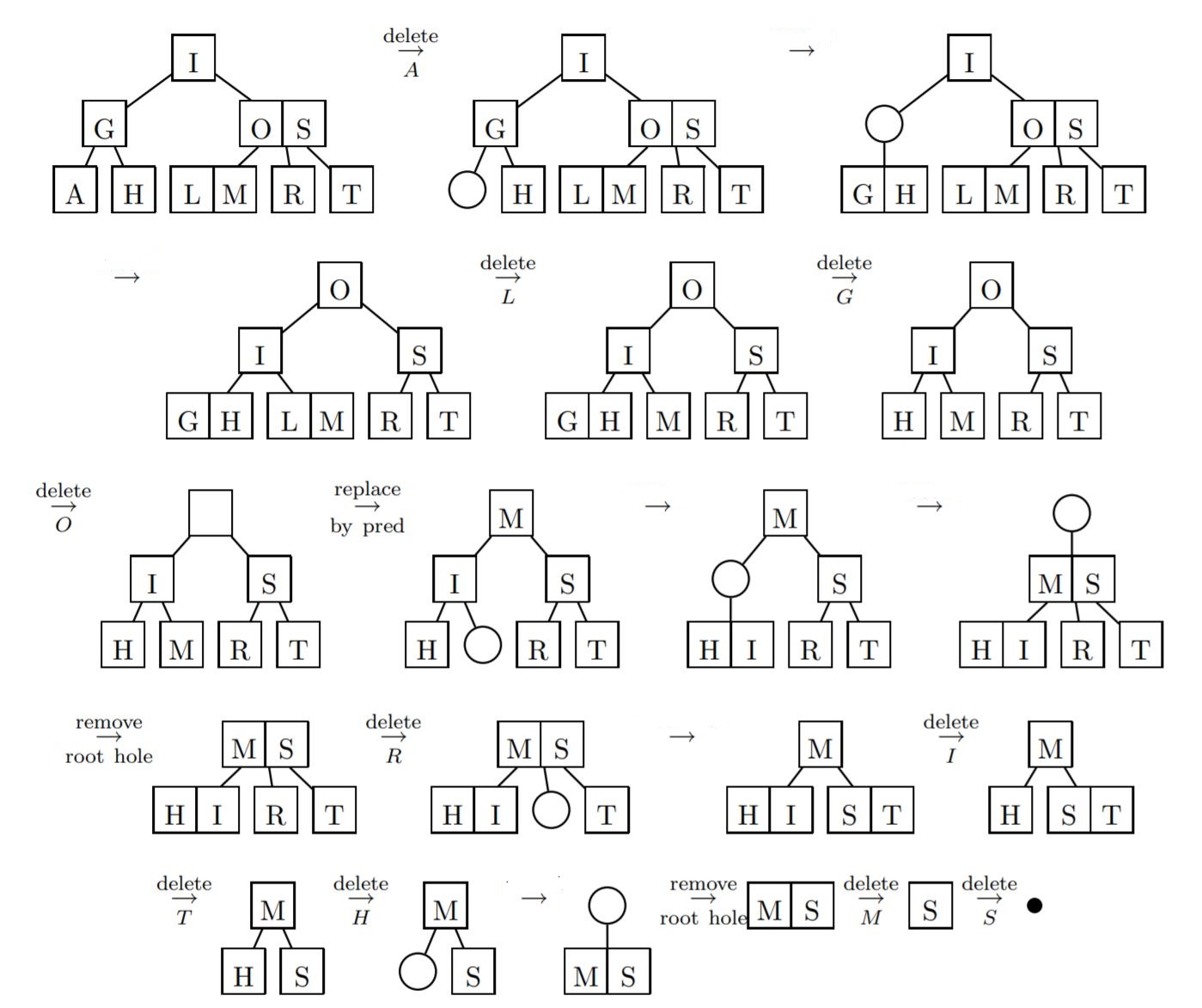
Here, we show the letter by letter deletion of the letters A L G O R I T H M S from the tree that is formed after inserting them.

The function to implement the delete operation.

void remove(node *candidate, t key) {
	if(!candidate) return; //If the key does not exist, we return
	if(candidate->contains(key)) {
		if(candidate->isleaf()) {
			candidate->remove(key); // Just remove if it is a leaf.
		}else {
            //We will have to rebalance and accordingly place the other nodes.
			if(key == *candidate->firstkey) {
				t *swap = findmaximum(candidate->less);
				delete candidate->firstkey;
				candidate->firstkey = new t(*swap);
				remove(candidate->less, *swap);
			}else {
                //We will have to rebalance and accordingly place the other nodes.
				t *swap = findminimum(candidate->great);
				delete candidate->secondkey;
				candidate->secondkey = new t(*swap);
				remove(candidate->great, *swap);
			}
		}
	}else {
		if(*candidate->firstkey > key) {
			remove(candidate->less, key); //Left subtree
		}else if(*candidate->firstkey <= key && candidate->is2node()) { //Mid subtree
			remove(candidate->btwn, key);
		}else {
			if(*candidate->secondkey > key) { //Right subtree
				remove(candidate->btwn, key);
			}else {
				remove(candidate->great, key);
			}

		}
	}
	merge(candidate); //Used to merge nodes incase of underflow.
}

Complexity of the operations

2-3 trees have an average and worst case time complexity of O(log n) (n is the number of data elements stored) for the search, insert and delete operations making this data structure a very efficient data storage method.

With this article at OpenGenus, you must have the complete idea of 2 3 Tree data structure. Enjoy.