AA trees were introduced by Arne Andersson in 1993 and hence the name AA. They are a type of balanced binary search trees. It was developed as a simpler alternative to red black trees.

It eliminates many of the conditions that need to be considered to maintain a red-black tree.

To understand AA trees, it is important to have a clear understanding of the concepts of a red black tree.

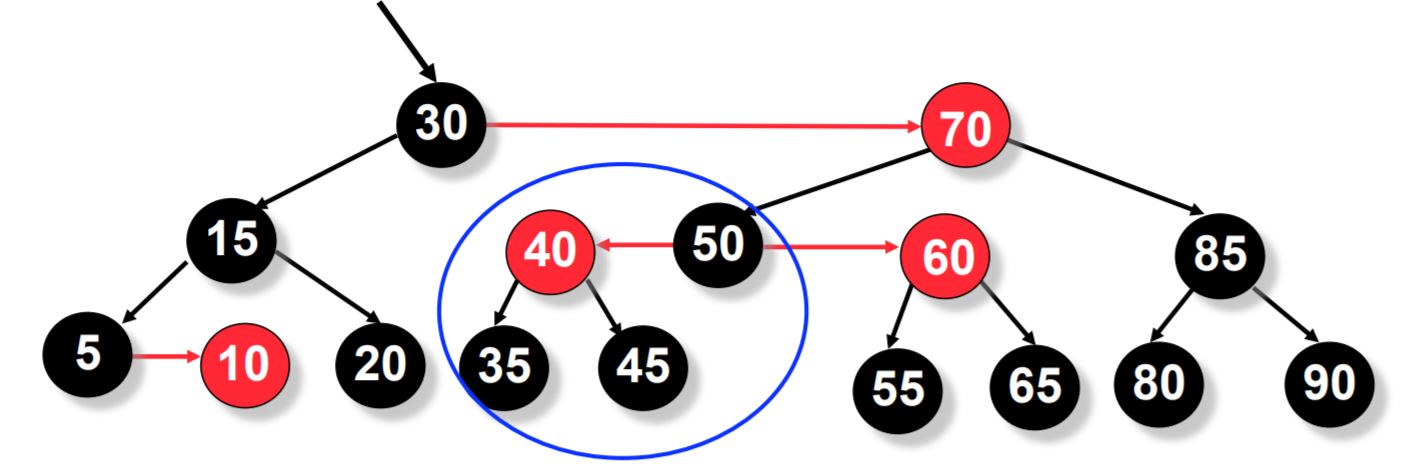
The tree below is an example of a red-black tree:

Properties of a red-black tree

1. Every node is either red or black.
2. The root node is always black.
3. Every leaf(NULL) is black.
4. If a node is red, then both its children are black.
5. Every simple path from a node to a descendant leaf contains the same number of black nodes.

If you would like more information about the operations on a red-black tree, do check out the below links

• Search Operation
• Insert Operation
• Delete Operation

AA Trees

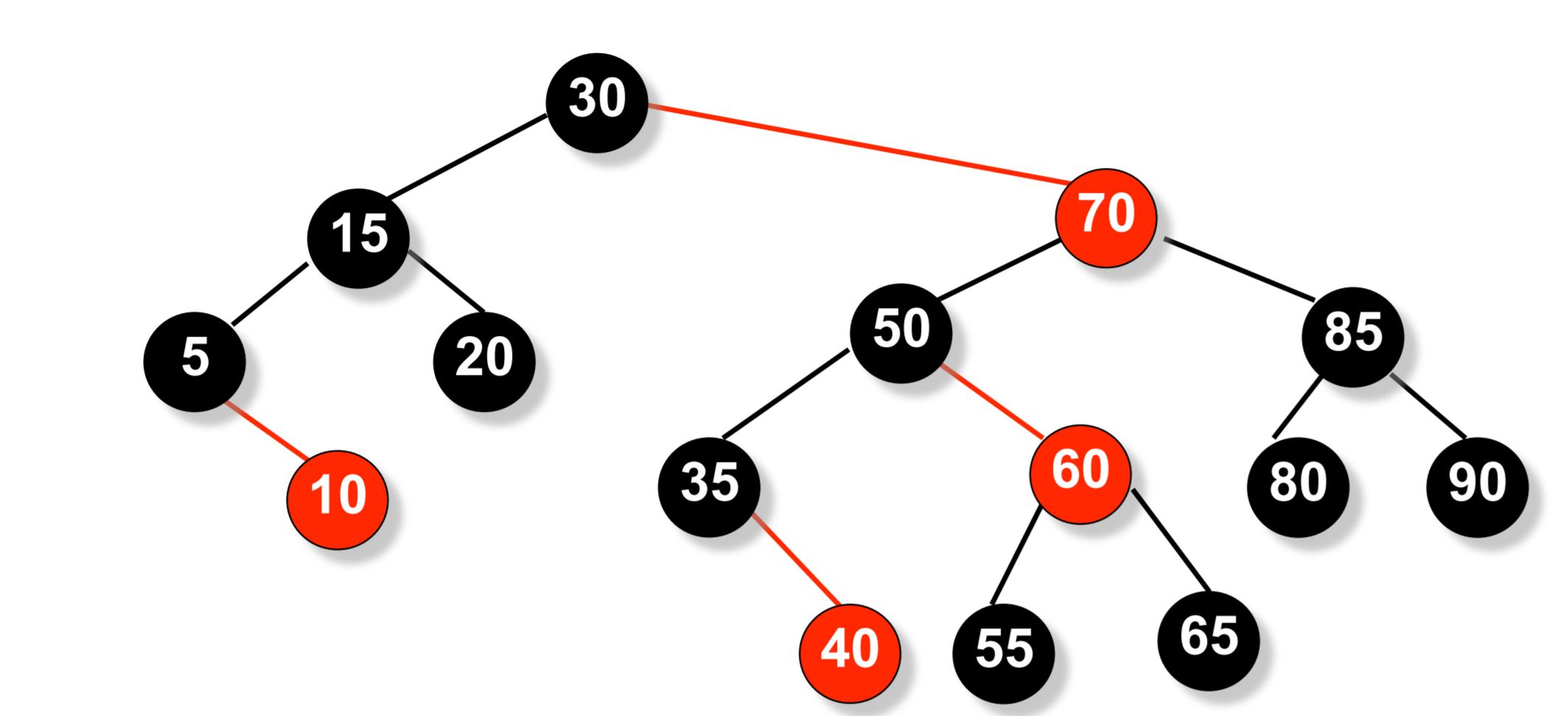
Unlike in red-black trees, red nodes on an AA tree can only be added as a right sub-child i.e. no red node can be a left sub-child. The tree below is an AA tree.

We can see from the above example that there are no left red children.
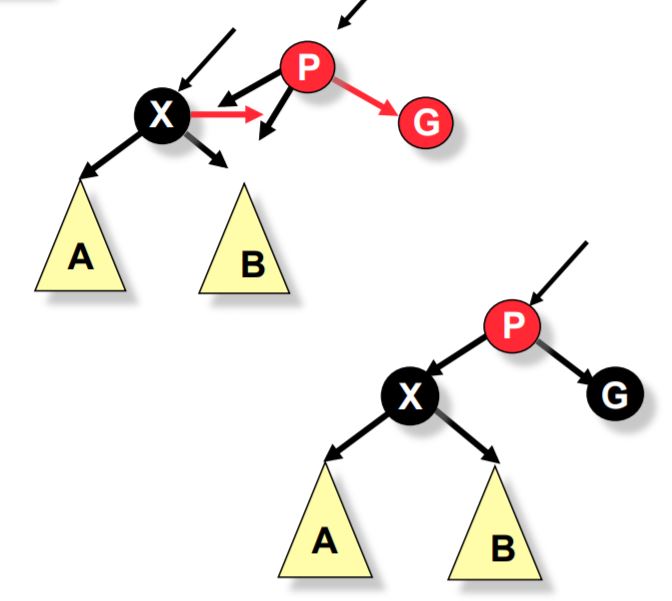
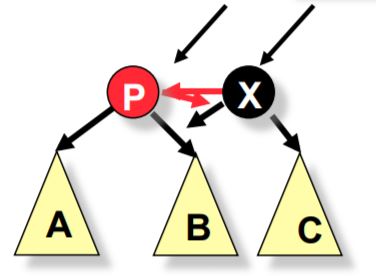
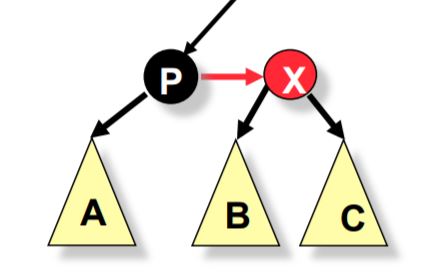
For the maintenance of a red-black tree, we need to consider seven different shapes to properly balance the tree:

An AA tree on the other hand needs to consider only two shapes due to the requirement that only right links can be red:

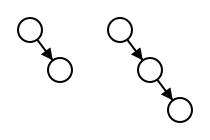
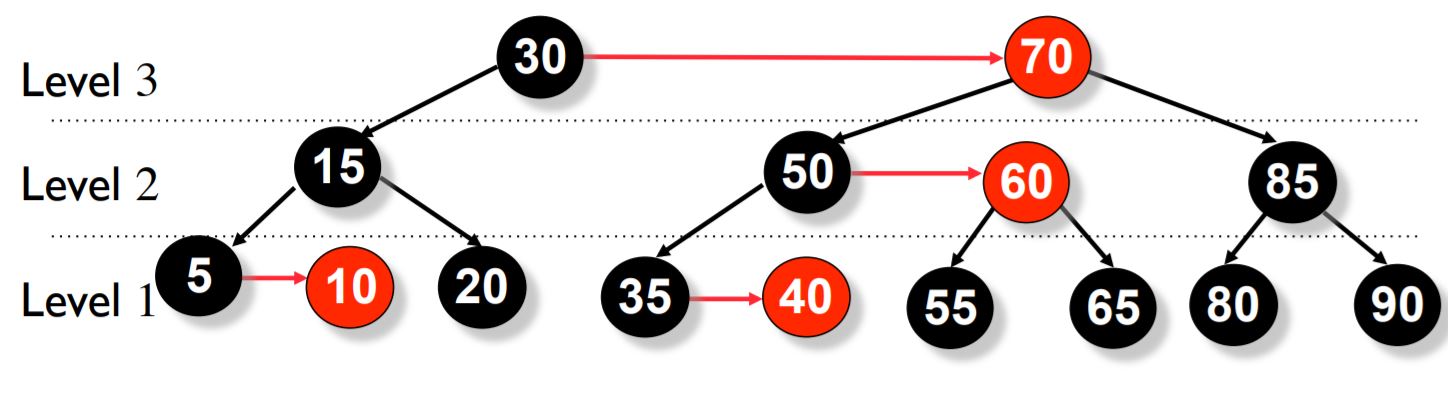
A level of a node is the number of left links to a NULL reference.
AA trees make use of the concept of levels to aid in the balancing of trees. The level of a node is used for the balancing of the tree instead of using the color.

The following five invariants hold for AA trees

1. The level of every leaf node is one.
2. The level of every left child is exactly one less than that of its parent.
3. The level of every right child is equal to or one less than that of its parent.
4. The level of every right grandchild is strictly less than that of its grandparent.
5. Every node of level greater than one, has two children.

Horizontal Link

A link where the child's level is equal to that of its parent is called a horizontal link. Horizontal links are always right links.
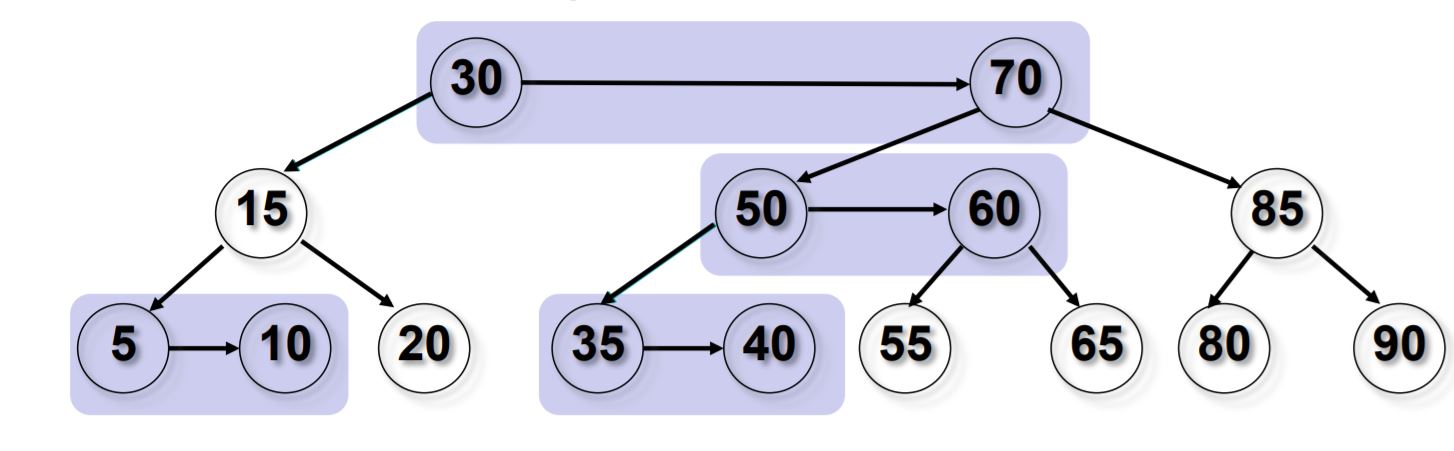
Red nodes are simply nodes that are located at the same level as their parents. For the AA tree shown above, the image below should help you understand which nodes are red and which are black and which are the horizontal links.

Operations on a AA tree

1. Search (Find) Operation
2. Insert Operation
3. Delete Operation

Search Operation

Since an AA tree is essentially a binary search tree, the search operation is the same as that of a binary serach tree. The fact that it is a balanced binary search tree, just makes the search operation more efficient.

Insert Operation

We will be making use of the split operation and the skew operation when we insert or delete an element from the tree.

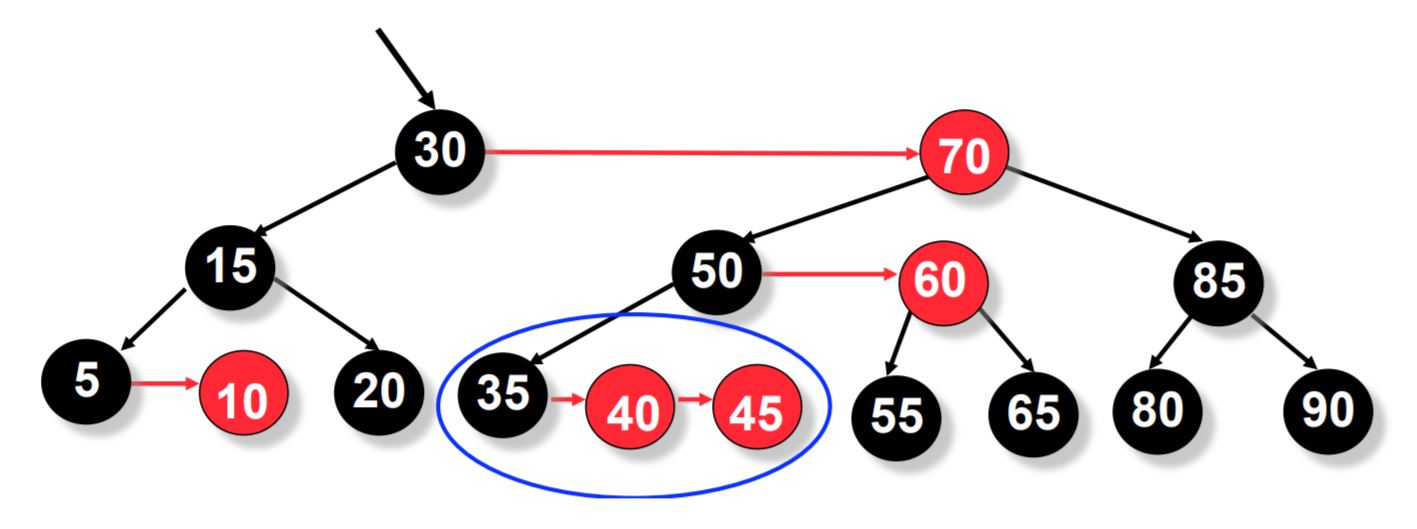
To explain thsis concept, let us insert 45 to this tree.

The steps to be followed are:

1. Insert every new node as a red node according to the rules of a Binary Search tree.
   
2. When we insert 45, we see that a double right-horizontal link is formed. We need to split the double right-horizontal link.

Split Operation

Here node G is the newly inserted element and it has violated one of the constraint of an AA tree. So to fix this, we make use of the split operation. Split is a simple left rotation between nodes X and P. By doing this, the level of P increases in the AA tree.

Psuedo code for the split operation

split(root)
{
    if root->right->right->level == root->level
        rotate_left(root)
}

Now after split, we again have a problem.

3. There is a left horizontal link at 50. If you recall from earlier, we are not supposed to have any left horizontal links in an AA tree. So now we make use of the skew operation.

Skew Operation

The skew operation invloves removing a left horizontal link in an AA tree.

Skew is a simple right rotation between X and P. Here P remains in the same level as before.

Psuedo code for the skew operation

skew(root)
{
    if root->left->level == root->level
        rotate_right(root)
}

Now after skew, we come back to the problem of double right horizontal links.

4. So we need to do a split operation.

5. Now after split, we get a left horizontal link at 70 and so we need to skew.

6. Now after skew, we again need to split because of a double horizontal link at 30.

7. After split at 30, we have finally completed the insertion of 45 to the tree.

As you can see from the process above, the insert operation is much simpler than that we have seen in a red-black tree. We make use of just 2 operations i.e. split and the skew operation.

Pseudo Code for Insert Operation

insert(Link &root, Node &add) {
    if (root == NULL) // have found where to insert y
        root = add;
    else if (add->key < root->key) // <= if duplicate ok
        insert(root->left, add);
    else if (add->key > root->key)
        insert(root->right, add);
    // else handle duplicate if not ok
    // do skew and split at each level
    
    skew(root); 
    split(root);
}

During insertion we do Skew first and then Split, this is because skew may cause double reds and then we do split if necessary. After a split, the middle node increases level, which may cause a problem for the original parent. So the parent may need to skew and then split.

Delete Operation

Rules to be followed while deleting a node from the tree:

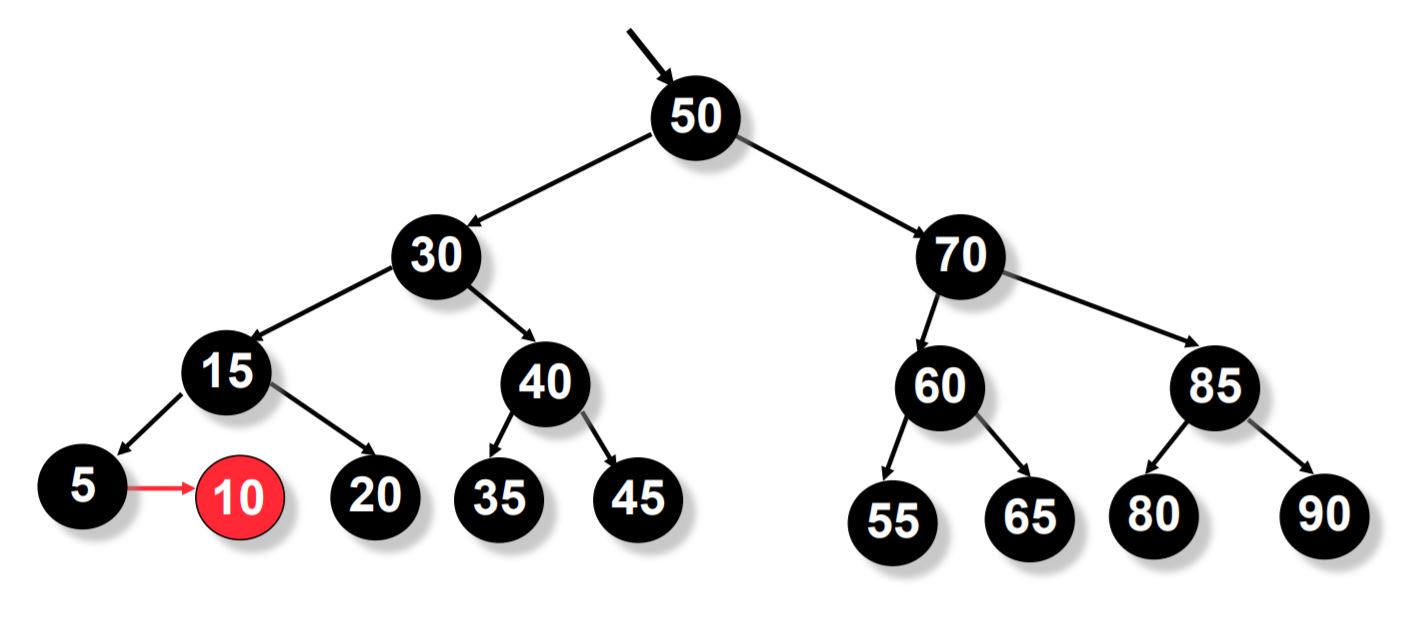
1. If the node to be deleted is a red leaf, just remove the leaf. For example in the above tree, node 10 is a red leaf. To delete that, just remove it and do not do any other changes.

2. If it is a parent to a single internal node, e.g. 5, it must be black. Replace with its child (must be red) and recolor child black.

3. If it has two internal-node children, swap node to be deleted with its in-order successor.

If in-order successor is red (must be leaf), remove leaf.
If in-order successor is a single child parent, then apply the second rule.

4. If in-order successor is a black leaf, or if the node to be deleted is a black leaf, we have to go through the below process.

Removal of a Black Leaf

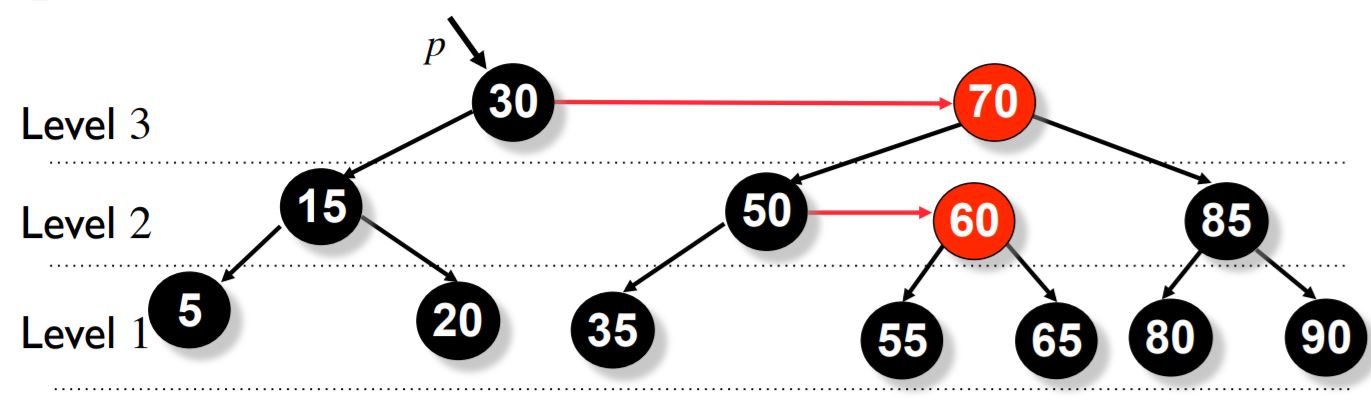
Follow the path from the removed node to the root. At each node p with 2 internal-node children do:

1. If either of p's children are 2 levels below p
   Decrease the level of p by one
   if p's right child was a red node, decrease its level too.
2. skew(p); skew(p->right); skew(p->right->right)
3. split(p); split(p->right).

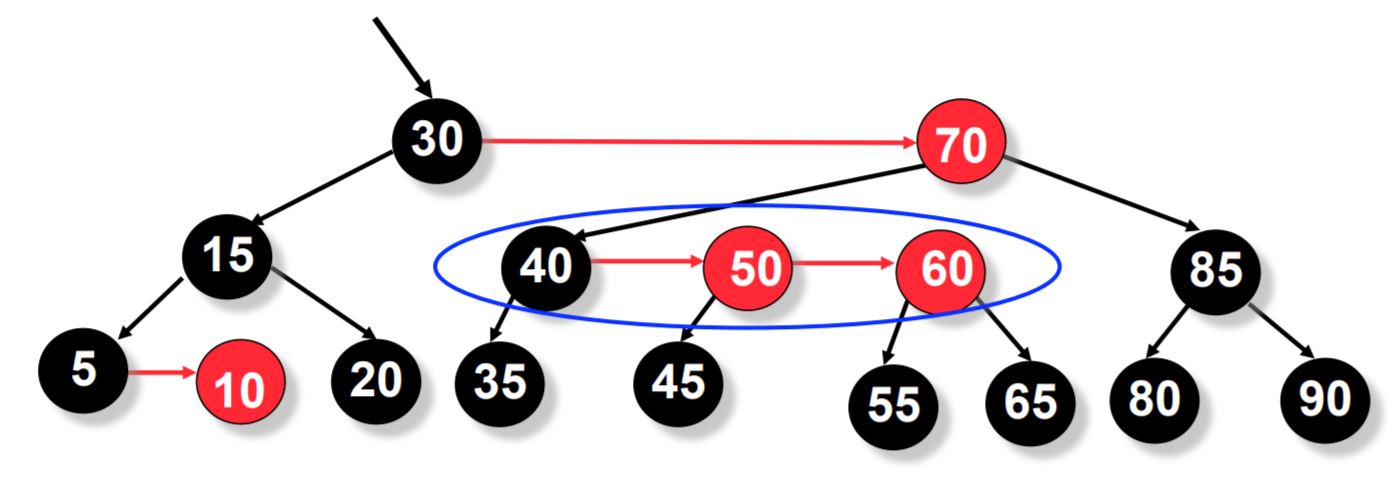
For an example let us delete node 5.

Here node 5 is a black leaf and hence we follow the below procedure to make the tree an AA tree after deletion.

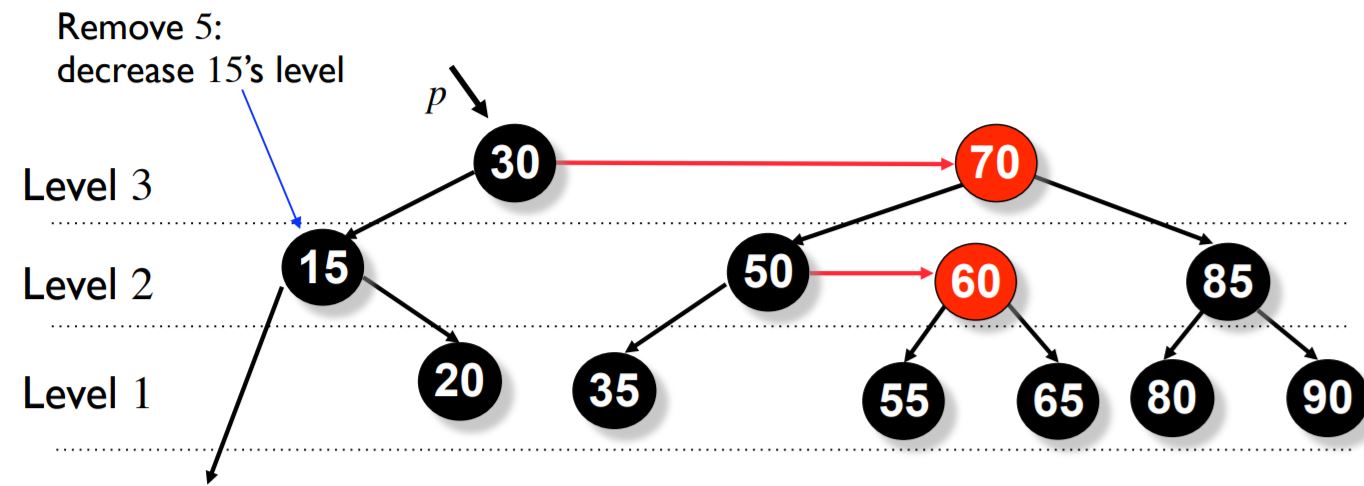
Now we decrease the level.

We follow the rules mentioned above and then decrese the level of p. Here p is a node with 2 internal children.

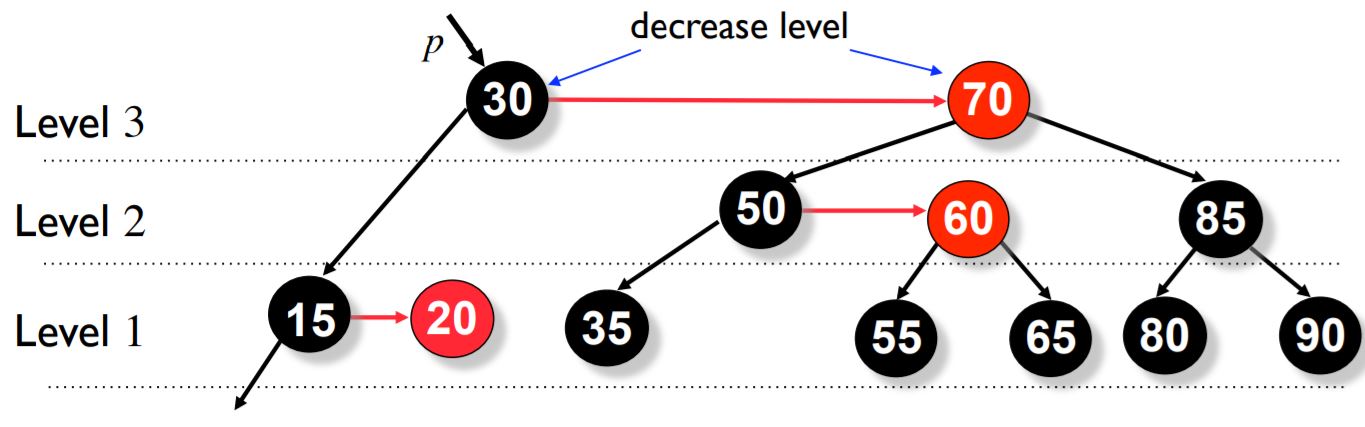
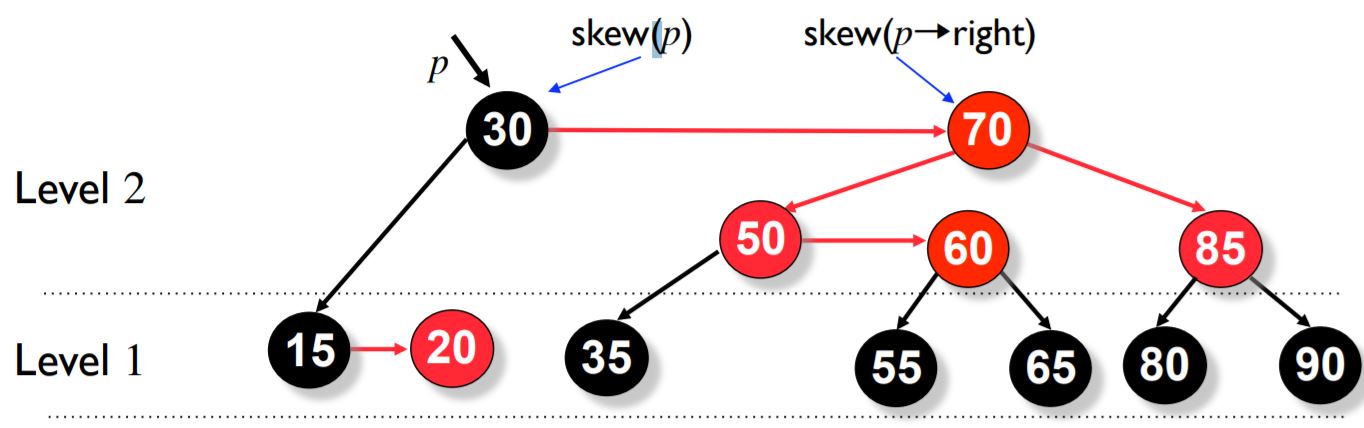
We now do the skew operation on p and p->right.

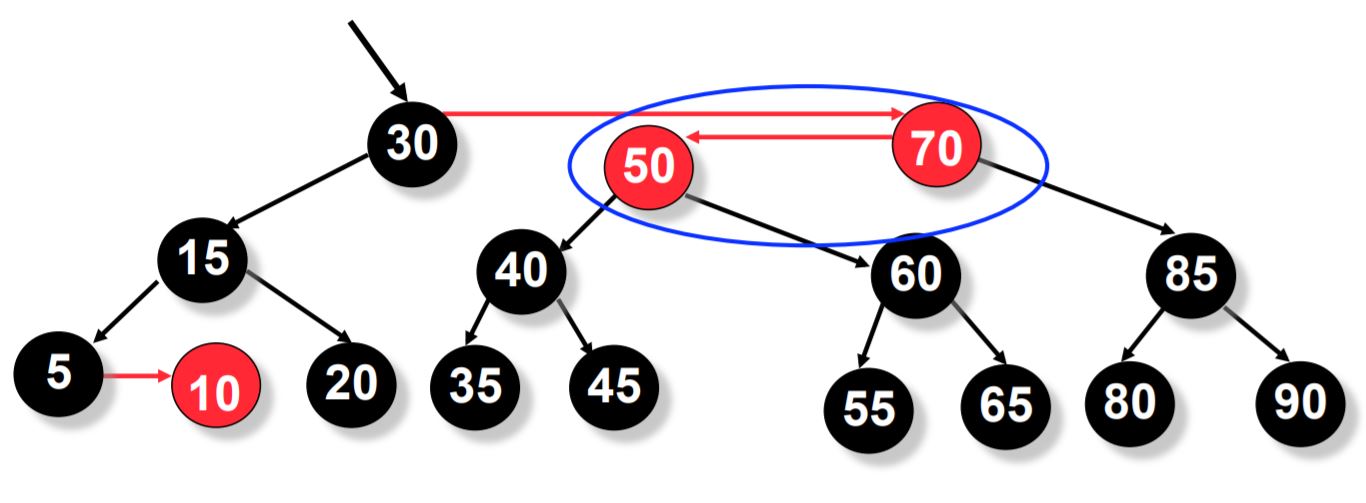
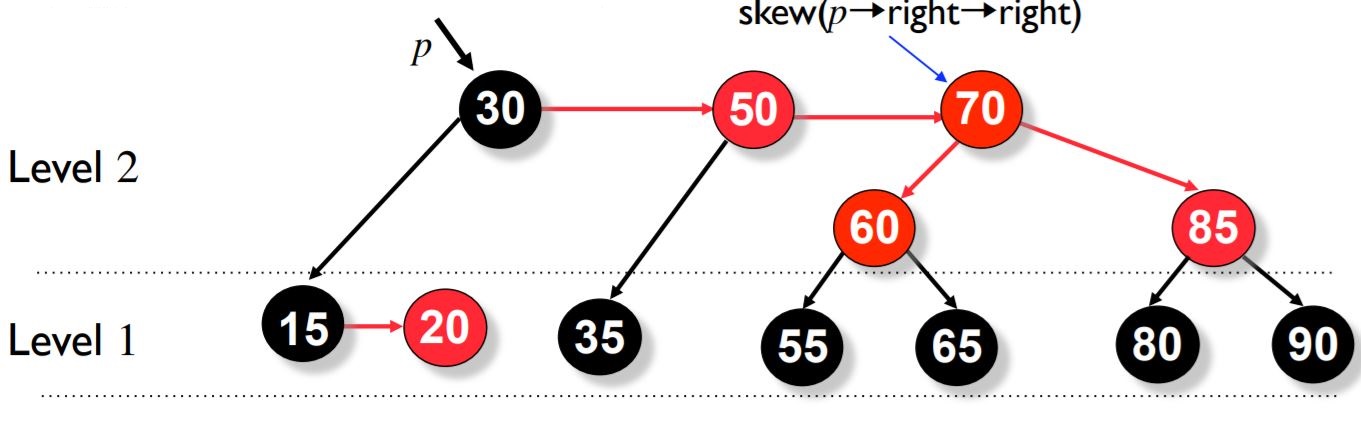
Now we do the skew operation on p->right->right.

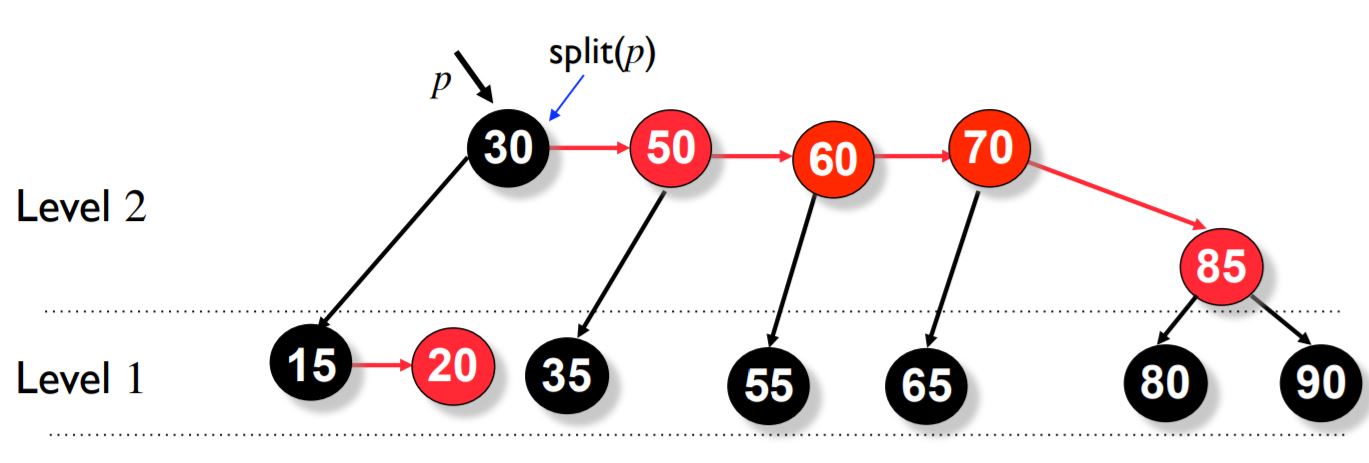
Now we do split operation on p.

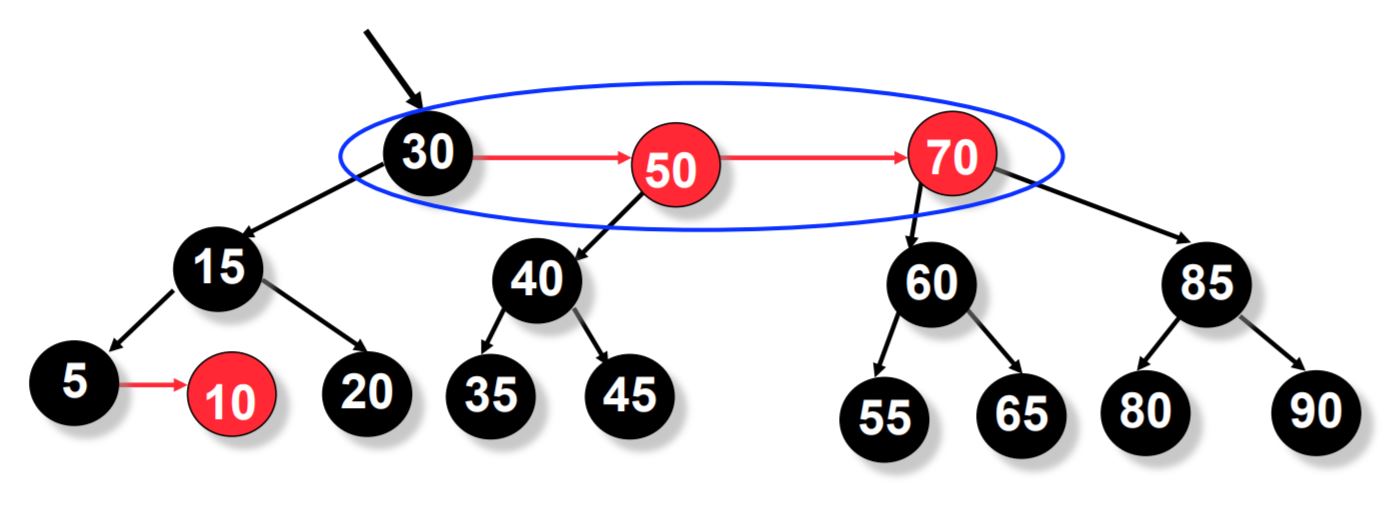
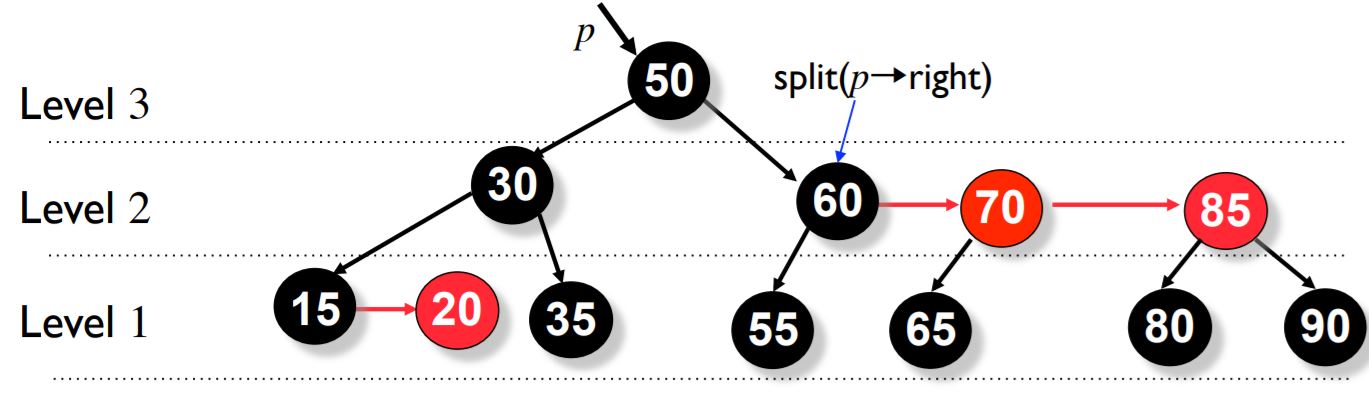
Now we do split operation on p->right.

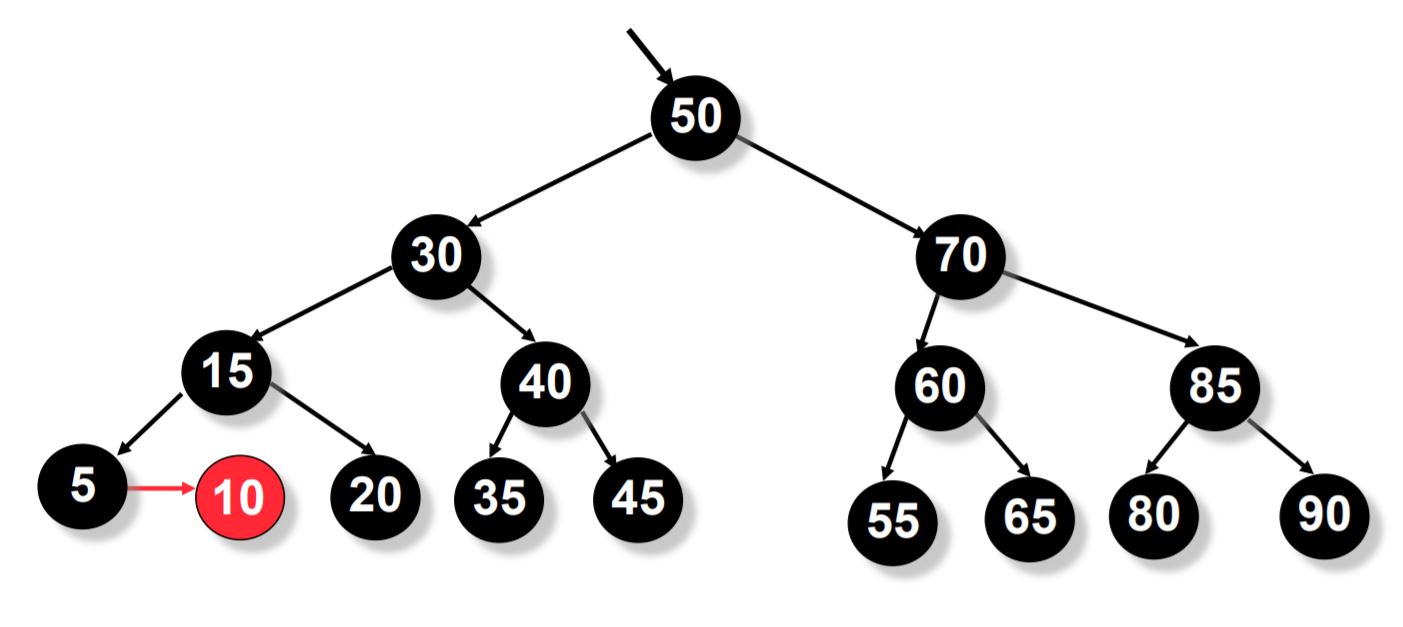
As you can see below, this tree is finally balanced and satisfies the properties of an AA tree.

Even in the worst case, it takes a maximum of 3 skew operations and 2 split operation. You can see this in the pseudo code below. This shows how much simpler an AA tree is compared to a red-black tree.

Psuedo code for the delete operation

//To rebalance the tree
if(root->left->level < root->level -1 || root->right->level < root->level -1)
{
    if(root->right->level > --root->level)
        root->right->level = root->level
    skew(root)
    skew(root->right)
    skew(root->right->right)
    split(root)
    split(root->right)
}

Conclusion

AA trees are self balacing binary search trees and guarantee fast operations in Θ(log n) time. The implementation code is also the shotest among all the balanced trees. It does this by eliminating half the restructuring process as we have already discussed above.

With this article at OpenGenus, you must have the complete idea of AA tree data structure and its various operations. Enjoy.