In this article, we have explained two approaches to find the Absolute value of Integer using Bitwise Operations namely Right shift, OR and XOR operations.

Contents

• Introduction
• Integers in binary
• Shifting bits
  • Positive Number
  • Negative Number
• XOR in binary
• Result
• A second approach
  • Sum Up

Introduction

If we define what's Absolute value, then it says that "The distance of some number from the zero is an Absolute Value".
Which means if there is some given number +/- N then the Absolute Value of this number should be N.

One way to find out the Absolute value of a number will be to check if the given value is negative or positive and if it's positive, then return n and if it's negative, then return n - 2*n.

Code for the above Example:

fn abs(n: i8) -> i8 {
    if n > 0 {
        n
    } else {
        (n - n) - n // Using this because,
        // Above mentioned can overflow.
    }
}

But, you see, this requires an if-else statement, and if we used binary operations to find Absolute Value, then one can avoid using if-else statements.

Note: we will be considering only 8-bit numbers here, but you can apply this method to others as well.
Just use size_of(n) * 8 to find out the number of bits for the data type you're using.

Integers in binary

I think if you're scrolling through this page, then you should already be familiar with how we represent integers in binary and how we know if a number is positive or negative but, to make sure that we're on the same page, we'll look at it once again.

There are two kinds of numbers one is signed and unsigned.

unsigned

• The range for unsigned numbers goes simply from 0 to 255 and in binary 0000_0000 to 1111_1111.

signed

• But the range for signed numbers goes from -128 to 127, and in binary, there are two ranges to make note of

  • 0 to 127 -> 0000_0000 to 0111_1111
  • -1 to -128 -> 1111_1111 to 1000_0000

Yep!! It counts backward.

And Of course, we will be using only signed integers here.

Shifting Bits

The rule is to have a 1 bit (the most left one) in signed integers as a sign bit, when it's 0 then, consider the number to be positive and negative if the sign bit is 1.

Now, shifting bits to the left will do the same things for both positive and negative integers.

But when we right shift the bits then, a positive integer will have no issue and, there will be a 0 in the sign bit before and even after the shift.
But, when we right shift a negative integer then, it is necessary that we make sure to preserve the sign bit. So, there will be 1 present in the sign bit.

For Example:

Positive Number

Let's consider a number n = 10 and, now if we right shift it, then it should look something like the given diagram:

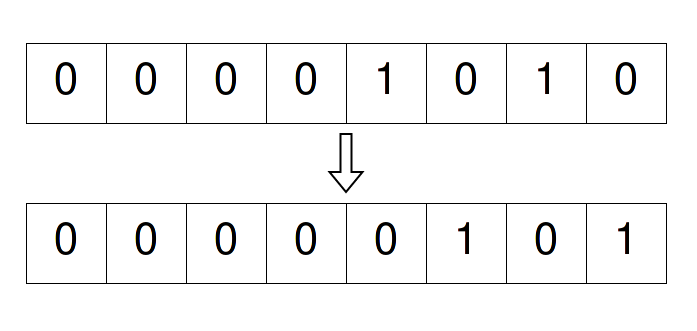
Negative Number

And for n = -10, it will look something like this:

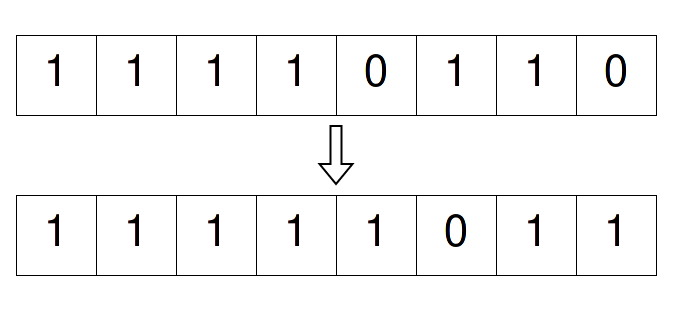
And if we think about this, then this thing gives us a really good trick to use, which will let us know if the given value of a number is negative or positive. How?

Well, if we right shift a positive integer then the bit that gets added to the left is 0, and for negative integer 1.

And if we keep doing the right shift then every bit in any negative number should become 1 and every bit in any positive number should become 0.

Therefore:

negative number >> 7 should give -1 (1111_1111).
positive number >> 7 should give 0 (0000_0000).

XOR in Binary

Here we are going to learn a trick regarding XOR operation, which is a necessary part to make a decision when we will be calculating the Absolute Value.

So, doing XOR operation is simple, only know that:

• if the given two bits are different then, the output will be 1.
• if the given two bits are same then, the output will be 0.

Now, let's try something where we consider some bits,

• a which, will be fixed to 1
  And
• b which, can be 1 or 0.
  So, if we take XOR for both 1 and 0 of b with a fixed bit a:
  Then,

0 ^ 1 = 1
1 ^ 1 = 0

So, we can conclude that for b, if XOR'ed with a, it should act as negation
that is, bit ^ 1 = !bit

And if we did same thing but, now a is fixed to 0, we see that:

0 ^ 0 = 0
1 ^ 0 = 1

then this tells us that,
bit ^ 0 = bit

And now, we can conclude that, if we take any number and XOR'ed it with a number where all bits are 1, then the result will be inverted version of the given number.

Example:

1 ^ 0b1111_1111 equals to -2
Remember, we're considering i8

Finding Absolute Value

Well, time to apply it all, to calculate Absolute Value the solution we have here can be divided in three steps:

1. Check if the number is negative or positive.
   For this, we can right shift the bits for the ( total number bits - 1 ). And this is our mask.

mask = n >> size_of(n) * 8 - 1

2. Add one to the number if negative and Add zero if positive.

Adding the mask will do this automatically.

n = n + mask
This step balances the number by filling the gap on the positive side of any unsigned number.

3. Now, invert the whole number using XOR if negative.
   Here also using mask should do this automatically because mask can choose to invert if the number is negative.

Example Code:

fn abs(n: i8) -> i8 {
    // 1st: right shift (sign check)
    let mask = n >> 7;
    
    // 2nd: Add the mask, `+` and `-` balance.
    let n = n + mask;
    
    // 3rd: Now, invert and return.
    n ^ mask
}

Time and Space Complexity

Assume we have to find the absolute value of a N-bit number

Time Complexity: O(N)

as the bitwise operations right shift and XOR along with add operation take O(N) time.

Space Complexity: O(N)

as we have to maintain the mask which is the same size of the input value.

Another Approach

When I was looking at 'the above' algorithm, I thought I would try to find some other way of doing this, So, after some tries, I figured one out, and when I told @aditya about this, he asked me to add it here.
So, here we are.

The idea for this approach is simple.

Whenever we multiply two different numbers then we make sure the signs are right and we have some rules for that. And one of them is, if we multiply two negative numbers then the result of this product should be a positive number.

And our goal is to change the number to positive if it's negative and return the same number if it's positive.

One thing we already learned is that if we use Right Shift we get

• -1 for negative numbers and,
• 0 for positive numbers.

So, if we use n >> 7 and multiply it with n, we can get a positive number for a given negative number.

Something like if n = -12:
then,

(n >> 7) * n will produce 12 as a result.

But you see if n = 12:
then,

(n >> 7) * n will produce 0 as a result.
Yep! A problem!

So, now we need to find a way which will change our mask to 1, when n >> 7 is 0 and do nothing when it's -1.

Let's look at the binary representation of -1, 0 and 1.

-1 --> 1111_1111
0 --> 0000_0000
1 --> 0000_0001

Here, we can see that we have to change the Right most bit to 1 if it's 0 or else all bits should remain 1.
And OR ( | ) is the operator that we can use for this task.

OR operator

So, what OR operator does is that, it returns 1 if any of the given input is 1, and it returns 0 only if bits of both sides are 0.

Now, if we try OR on our mascots -1 and 0, with 1, we get the following result:

-1 | 1 --> 1111_1111
0 | 1 --> 0000_0001

Their we go we got it.

Sum Up

Now, if we sum up all that, then again we have 3 Steps to do this:

1. Check, if the given number n is negative or positive.

if_neg = n >> size_of(n) * 8 - 1

2. Create mask. For that take the OR of if_neg and 1 (0000_0001).

mask = if_neg | 1

3. Now take product of the mask and the Number n to get the Absolute Value.

mask * n

Code Example

    fn abs(n: i8) -> i8 {
        let size = std::mem::size_of_val(n) * 8;
        
        // 1st step: do the right_shift
        let if_neg = n >> (size - 1);
        
        // 2nd step: change to 1 if 0 else remain -1
        let mask = if_neg | 1_i8;
        
        // 3rd step: multiply and return
        mask * n
    }

Time and Space Complexity

Assume we have to find the absolute value of a N-bit number

• Time Complexity: O(N logN)

as the bitwise operations right shift and OR take O(N) time
but the arithmetic operation Multiplication has a theoretical limit of O(N logN). In practice, the Time Complexity of Multiplication is O(N²).

In practice, the Time Complexity of this approach is O(N²) while the theoretical limit is O(N logN).

• Space Complexity: O(N)

as we have to maintain the mask which is the same size of the input value.

With this article at OpenGenus, you must have the complete idea of Absolute value of Integer using Bitwise Operations.