
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
A B+ tree is an N-ary tree with a variable but often large number of children per node. A B+ tree consists of a root, internal nodes and leaves. The root may be either a leaf or a node with two or more children.
A B+ tree can be viewed as a B-tree in which each node contains only keys (not key–value pairs), and to which an additional level is added at the bottom with linked leaves.
The B+-Tree consists of two types of nodes:
- internal nodes
- leaf nodes
Properties:
- Internal nodes point to other nodes in the tree.
- Leaf nodes point to data in the database using data pointers. Leaf nodes also contain an additional pointer, called the sibling pointer, which is used to improve the efficiency of certain types of search.
- All the nodes in a B+-Tree must be at least half full except the root node which may contain a minimum of two entries. The algorithms that allow data to be inserted into and deleted from a B+-Tree guarantee that each node in the tree will be at least half full.
- Searching for a value in the B+-Tree always starts at the root node and moves downwards until it reaches a leaf node.
- Both internal and leaf nodes contain key values that are used to guide the search for entries in the index.
- The B+ Tree is called a balanced tree because every path from the root node to a leaf node is the same length. A balanced tree means that all searches for individual values require the same number of nodes to be read from the disc.
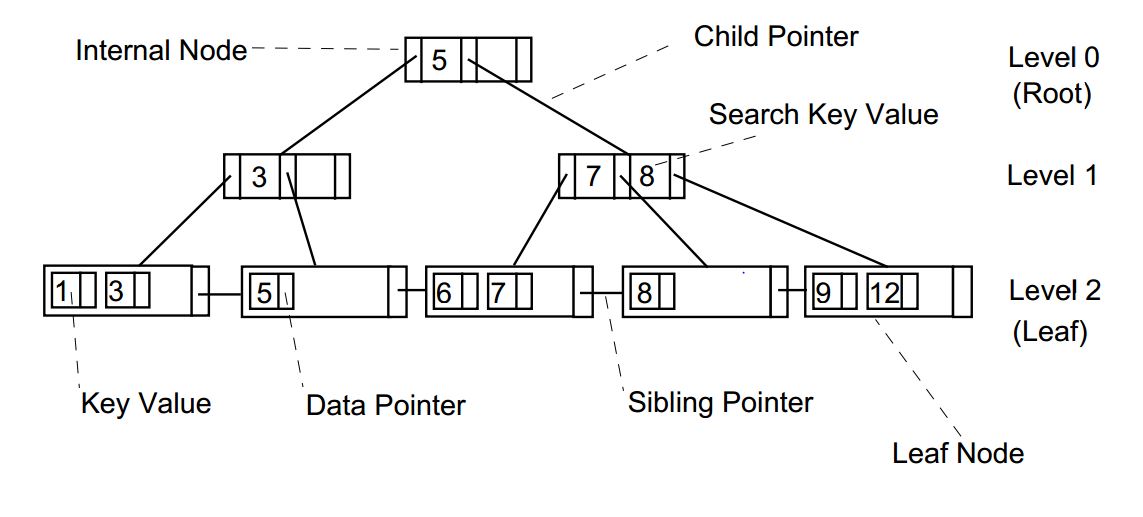
The figure depicts the basic structure of B+ Tree.
Algorithm
- Basic operations associated with B+ Tree:
-
Searching a node in a B+ Tree
- Perform a binary search on the records in the current node.
- If a record with the search key is found, then return that record.
- If the current node is a leaf node and the key is not found, then report an unsuccessful search.
- Otherwise, follow the proper branch and repeat the process.
-
Insertion of node in a B+ Tree:
- Allocate new leaf and move half the buckets elements to the new bucket.
- Insert the new leaf's smallest key and address into the parent.
- If the parent is full, split it too.
- Add the middle key to the parent node.
- Repeat until a parent is found that need not split.
- If the root splits, create a new root which has one key and two pointers. (That is, the value that gets pushed to the new root gets removed from the original node)
-
Deletion of a node in a B+ Tree:
- Descend to the leaf where the key exists.
- Remove the required key and associated reference from the node.
- If the node still has enough keys and references to satisfy the invariants, stop.
- If the node has too few keys to satisfy the invariants, but its next oldest or next youngest sibling at the same level has more than necessary, distribute the keys between this node and the neighbor. Repair the keys in the level above to represent that these nodes now have a different “split point” between them; this involves simply changing a key in the levels above, without deletion or insertion.
- If the node has too few keys to satisfy the invariant, and the next oldest or next youngest sibling is at the minimum for the invariant, then merge the node with its sibling; if the node is a non-leaf, we will need to incorporate the “split key” from the parent into our merging.
- In either case, we will need to repeat the removal algorithm on the parent node to remove the “split key” that previously separated these merged nodes — unless the parent is the root and we are removing the final key from the root, in which case the merged node becomes the new root (and the tree has become one level shorter than before).
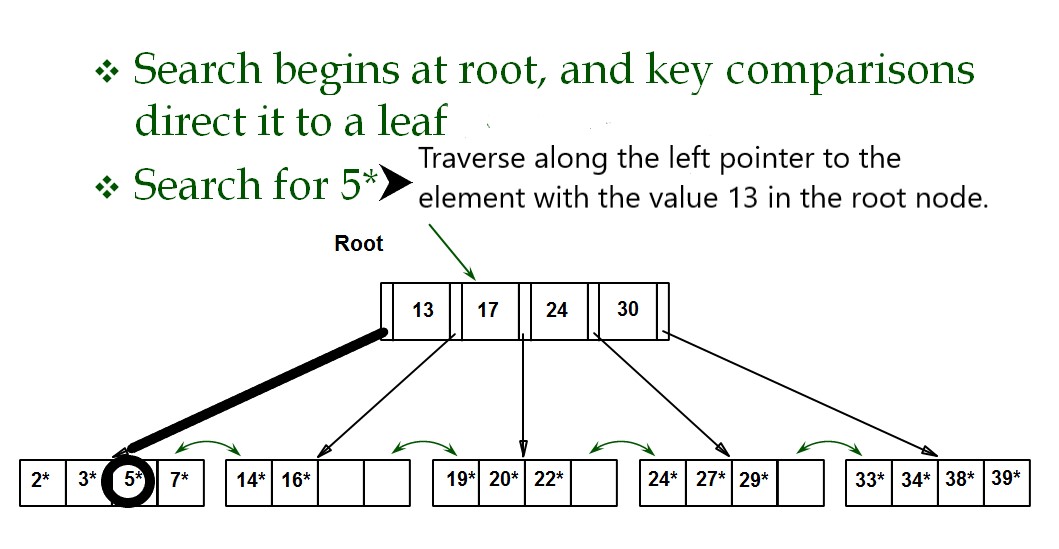
The figure depicts the searching of an element in a B-Tree.
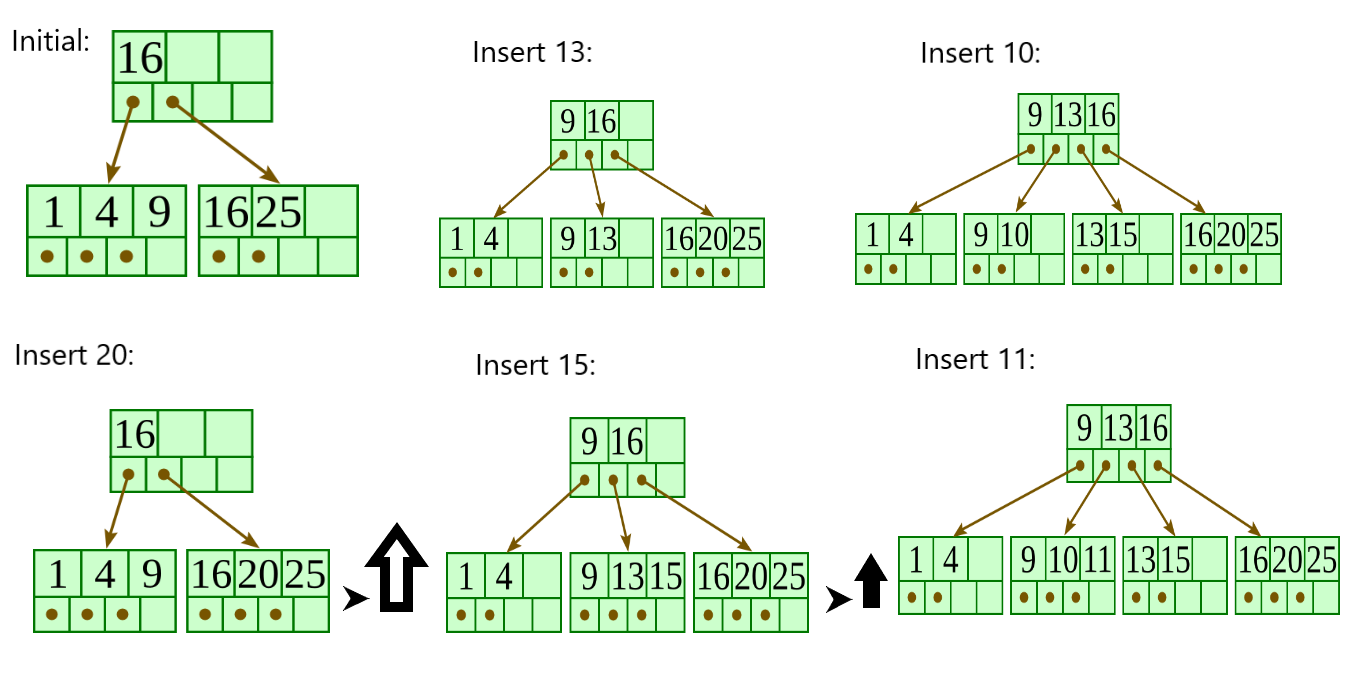
**The figure illustrates the insertion of an element in a B+ Tree. B+ tree grows at the root and not at the leaves.**
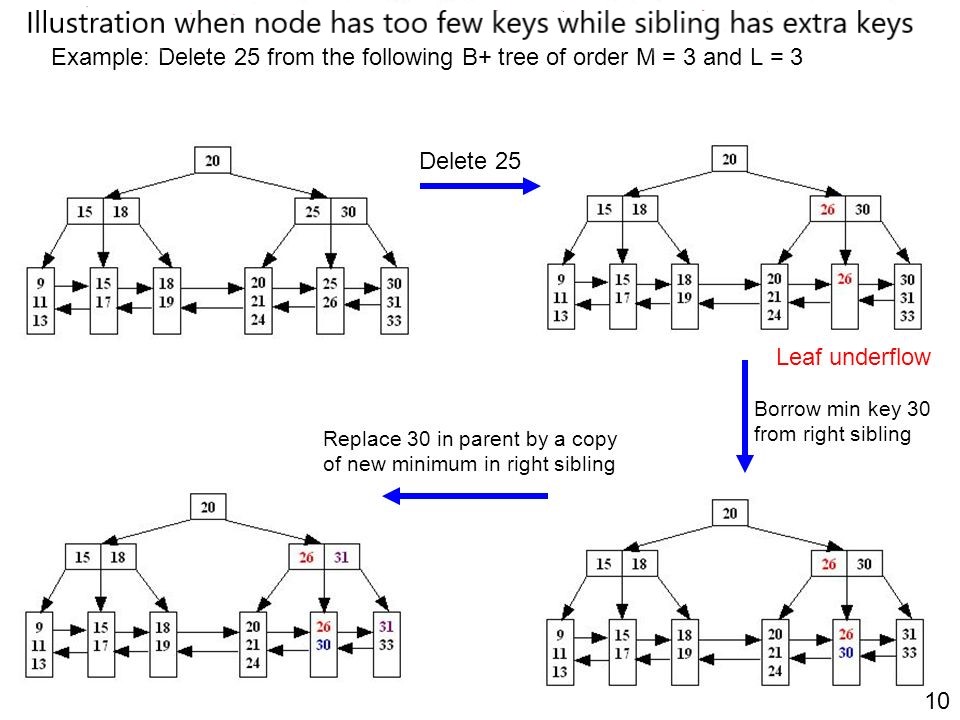
The figure illustrates the deletion of an element from a b+ tree.
Complexity
-
Worst case search time complexity:
Θ(logn) -
Average case search time complexity:
Θ(logn) -
Best case search time complexity:
Θ(logn) -
Worst case insertion time complexity:
Θ(logn) -
Worst case deletion time complexity:
Θ(logn) -
Average case Space complexity:
Θ(n) -
Worst case Space complexity:
Θ(n)
Pseudocode
Searching
1) Apply Binary search on records.
2) If record with the search key is found
return required record
Else if current node is leaf node and key not found
print Element not Found
Insertion
1) If the bucket is not full (at most b 1 entries after the insertion), add the record.
2) Otherwise, split the bucket.
1) Allocate new leaf and move half the buckets elements to the new bucket.
2) Insert the new leafs smallest key and address into the parent.
3) If the parent is full, split it too.
1) Add the middle key to the parent node.
4) Repeat until a parent is found that need not split.
3) If the root splits, create a new root which has one key and two pointers. (That is, the value that gets pushed to the new root gets removed from the original node)
Deletion
1) Start at the root and go up to leaf node containing the key K
2) Find the node n on the path from the root to the leaf node containing K
A. If n is root, remove K
a. if root has mode than one keys, done
b. if root has only K
i) if any of its child node can lend a node
Borrow key from the child and adjust child links
ii) Otherwise merge the children nodes it will be new root
c. If n is a internal node, remove K
i) If n has at lease ceil(m/2) keys, done!
ii) If n has less than ceil(m/2) keys,
If a sibling can lend a key,
Borrow key from the sibling and adjust keys in n and the parent node
Adjust child links
Else
Merge n with its sibling
Adjust child links
d. If n is a leaf node, remove K
i) If n has at least ceil(M/2) elements, done!
In case the smallest key is deleted, push up the next key
ii) If n has less than ceil(m/2) elements
If the sibling can lend a key
Borrow key from a sibling and adjust keys in n and its parent node
Else
Merge n and its sibling
Adjust keys in the parent node
Implementations
#include<stdio.h>
#include<conio.h>
#include<iostream>
using namespace std;
struct B+TreeNode
{
int *data;
B+TreeNode **child_ptr;
bool leaf;
int n;
}*root = NULL, *np = NULL, *x = NULL;
B+TreeNode * init()
{
int i;
np = new B+TreeNode;
np->data = new int[5];
np->child_ptr = new B+TreeNode *[6];
np->leaf = true;
np->n = 0;
for (i = 0; i < 6; i++)
{
np->child_ptr[i] = NULL;
}
return np;
}
void traverse(B+TreeNode *p)
{
cout<<endl;
int i;
for (i = 0; i < p->n; i++)
{
if (p->leaf == false)
{
traverse(p->child_ptr[i]);
}
cout << " " << p->data[i];
}
if (p->leaf == false)
{
traverse(p->child_ptr[i]);
}
cout<<endl;
}
void sort(int *p, int n)
{
int i, j, temp;
for (i = 0; i < n; i++)
{
for (j = i; j <= n; j++)
{
if (p[i] > p[j])
{
temp = p[i];
p[i] = p[j];
p[j] = temp;
}
}
}
}
int split_child(B+TreeNode *x, int i)
{
int j, mid;
B+TreeNode *np1, *np3, *y;
np3 = init();
np3->leaf = true;
if (i == -1)
{
mid = x->data[2];
x->data[2] = 0;
x->n--;
np1 = init();
np1->leaf = false;
x->leaf = true;
for (j = 3; j < 5; j++)
{
np3->data[j - 3] = x->data[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->data[j] = 0;
x->n--;
}
for(j = 0; j < 6; j++)
{
x->child_ptr[j] = NULL;
}
np1->data[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
root = np1;
}
else
{
y = x->child_ptr[i];
mid = y->data[2];
y->data[2] = 0;
y->n--;
for (j = 3; j < 5; j++)
{
np3->data[j - 3] = y->data[j];
np3->n++;
y->data[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a)
{
int i, temp;
x = root;
if (x == NULL)
{
root = init();
x = root;
}
else
{
if (x->leaf == true && x->n == 5)
{
temp = split_child(x, -1);
x = root;
for (i = 0; i < (x->n); i++)
{
if ((a > x->data[i]) && (a < x->data[i + 1]))
{
i++;
break;
}
else if (a < x->data[0])
{
break;
}
else
{
continue;
}
}
x = x->child_ptr[i];
}
else
{
while (x->leaf == false)
{
for (i = 0; i < (x->n); i++)
{
if ((a > x->data[i]) && (a < x->data[i + 1]))
{
i++;
break;
}
else if (a < x->data[0])
{
break;
}
else
{
continue;
}
}
if ((x->child_ptr[i])->n == 5)
{
temp = split_child(x, i);
x->data[x->n] = temp;
x->n++;
continue;
}
else
{
x = x->child_ptr[i];
}
}
}
}
x->data[x->n] = a;
sort(x->data, x->n);
x->n++;
}
int main()
{
int i, n, t;
cout<<"enter the no of elements to be inserted\n";
cin>>n;
for(i = 0; i < n; i++)
{
cout<<"enter the element\n";
cin>>t;
insert(t);
}
cout<<"traversal of constructed tree\n";
traverse(root);
getch();
}
Applications
Importance of B+ Tree:
-
Using B+, we can retrieve range retrieval or partial retrieval. Traversing through the tree structure makes this easier and quicker.
-
As the number of record increases/decreases, B+ tree structure grows/shrinks. There is no restriction on B+ tree size, like we have in ISAM.
-
Since we have all the data stored in the leaf nodes and more branching of internal nodes makes height of the tree shorter. This reduces disk I/O. Hence it works well in secondary storage devices.
