Aho Corasick Algorithm

Reading time: 25 minutes | Coding time: 15 minutes

Naive Approach

The obvious and naive approach is to just search each pattern in the string at every possible position but this will yield time complexity of O(n * m). Now, if you know the KMP Algorithm, it gives complexity of O(n+m). But, KMP works when there is a single pattern and single text string. So, for k patterns : Time Complexity is O(n + k*m) which is still decent for a few number of patterns of small lengths. As the length and number of patterns increases time taken by KMP will also increase. So, we need something else here.

Efficient Approach

To solve this problem efficiently we need a tree like data structure called Trie. It is an efficient data structure to represent multiple strings. We can construct a trie out of our pattern strings.

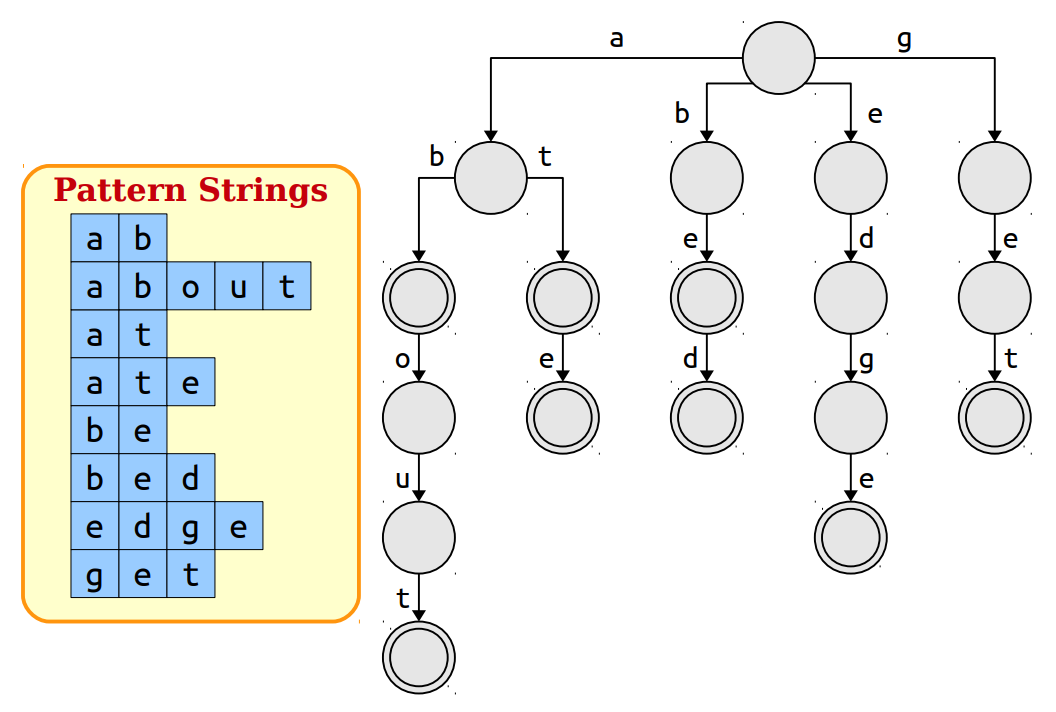
We can mark all the nodes where the strings end and then run our pattern searching. There are many ways to implement the trie but on average it takes linear time to build a trie. But overall time comlexity of searching patterns using trie is still O(m * Lmax) where L_max is maximum length of pattern. We need something else to make this more efficient.

Suffix/Failure Links

The main problem with our previous approach is that when we follow the trie and suppose at any point we don't have further nodes to follow i.e. pattern might not exist thereafter, we will have to start from the root of trie again. To avoid starting again and again from root after every mismatch we can follow node which share the longest suffix with our current node. Longest common suffix will guarantee that we don't need to check that much string again and we continue right after every mismatch. These links which point to node which esssentially are the longest suffix are called suffix links or failure links because we use them in case when wwe fail to match the current character with any node on our current path on trie.

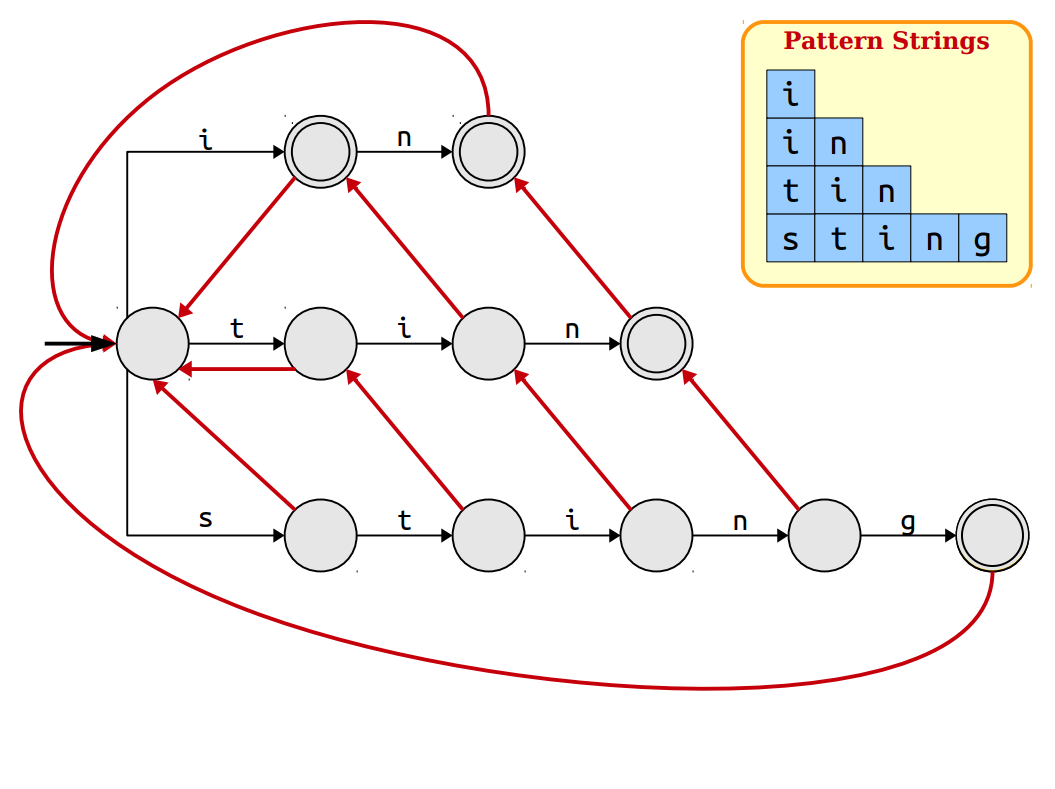
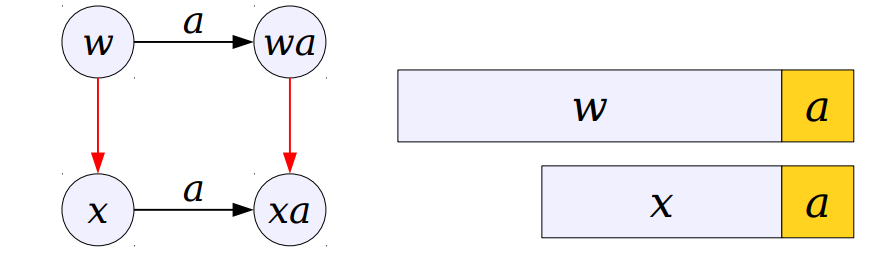
If we can compute our suffix links efficiently we can do our search in O(m) time. Suppose there is a string w with longest common suffix as a string x in trie. Now if we want a suffix link for string "wa" we can check x , if it has a node with character 'a' as it child we can make "xa" a suffix link of "wa".

If "xa" doesn't exist we will now follow x's suffix because if "x" is a suffix of "w" then a suffix of "x" will also be a suffix of "w".

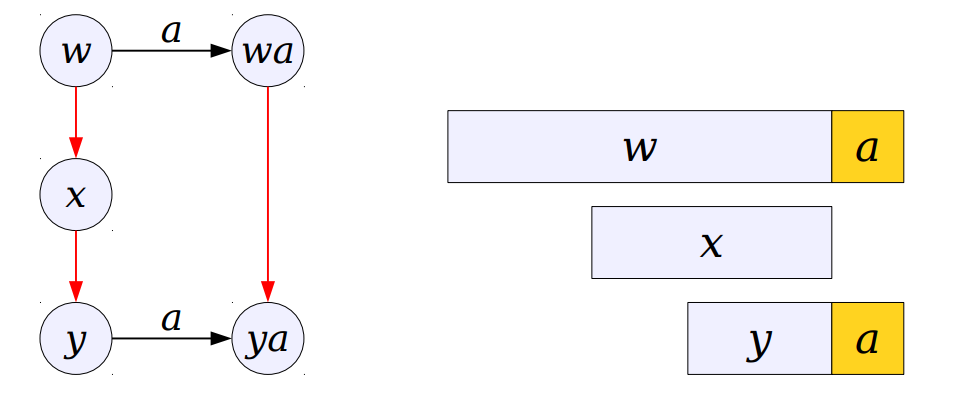
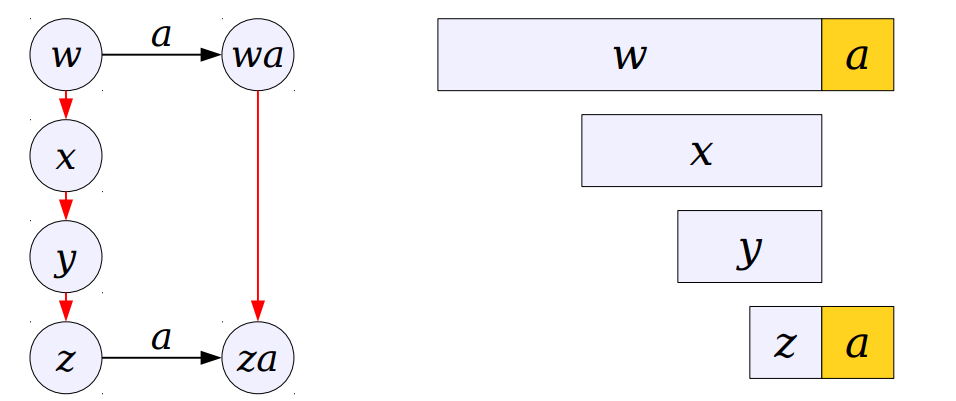
It is evident we do this until we find proper link or conclude that such link doesn't exist. In that case, our suffix link will point back to root. In the picture above links of red colour are appropriate suffix link for that particular trie.

Output Links

Their is one more problem with our approach that needs to be addressed. When we were building suffix links, you've noticed that we will miss some patterns when one pattern is possibly a suffix of another pattern. So, for every node in trie we will also need a output link which points to the possible patterns occuring at that position. This will form a linked list at every node pointing to every possible pattern occurring at that position.

To construct output link we need to see suffix links. As the suffix link points to pattern sharing longest common suffix, that suffix might be the pattern. If it is indeed a pattern we will point the output link to the same node where suffix links points and if not we will point output link to the suffix link node's output link.

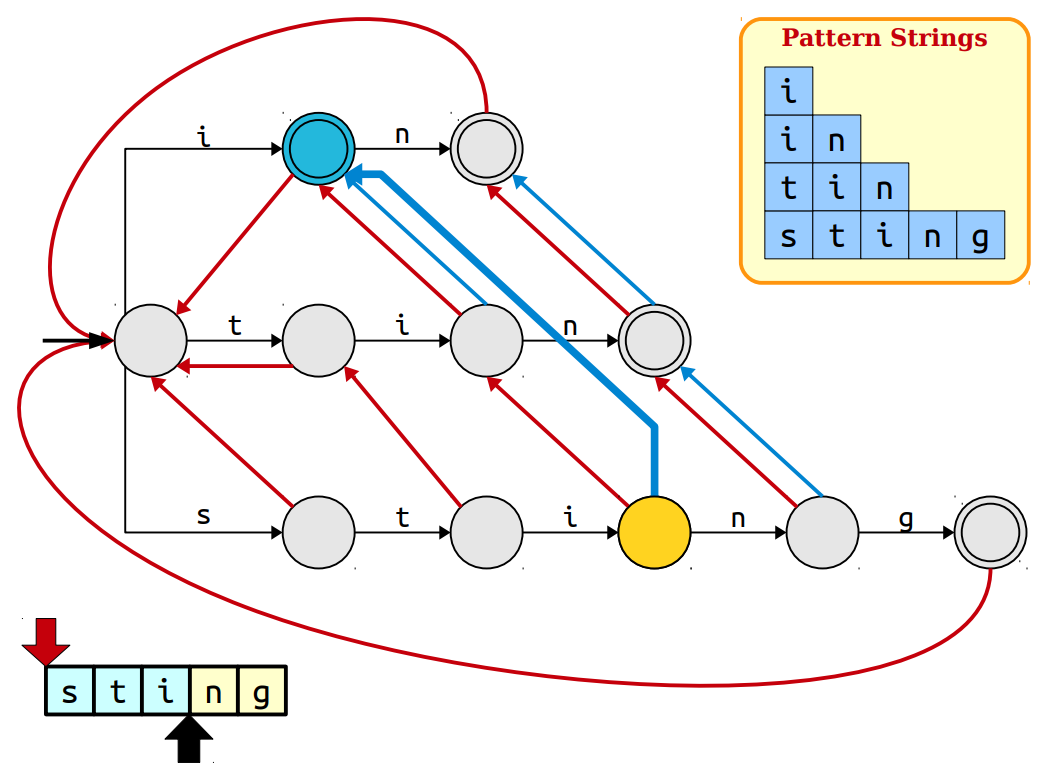
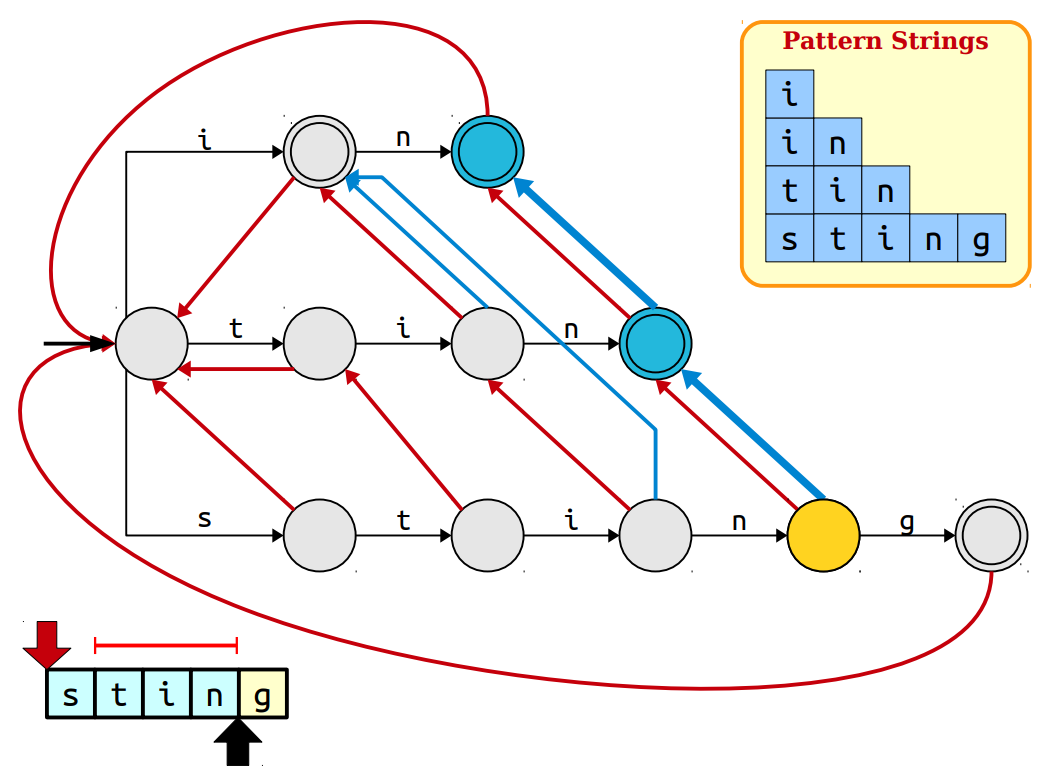
Now, we are all set to use our trie which is a automata. In a way we formed an automata where we change our states according to input. This matching will be done in O(m + z) time complexity where z is number of occurrences. If you've not noticed, both the suffix links construction and output links construction will be done using Breadth First Search as our computations depend on the previous level node.

Pseudocode

1. Construct a trie out of input patterns.
2. Construct suffix and output links in Breadth First Order.
3. Use the constructed automata to traverse the string.
4. If current character matches any of children then follow it otherwise follow the suffix link.
5. At every node follow the output links to get patterns occurring till the current position.

Time Complexity

Trie Contruction: O(n)
Suffix/Output Link Construction: O(n)
Searching: O(m + z)

Time Complexity: O(n + m + z)

where z is number of occurrences

Implementation

There are many ways to implement trie. You may choose whichever suits your needs or whichever you may find easy. In this post I've used maps to implement trie but similarly arrays, hash tables, linked list etc. can be used. Note: According to the method used to implement trie time complexity may vary. Here, we are considering O(n) time construction of trie.

#include <iostream>
#include <vector>
#include <map>
#include <queue>
using namespace std;

struct trie_node{ // structure of trie node
    map<char, trie_node*> child;
    trie_node* suffix_link;
    trie_node* output_link;
    int pattern_ind;
};

typedef struct trie_node node;

node* add_node(){ // to add new trie node
    node* temp = new node; // allocating memory for new trie node

    // assigning default values
    temp ->suffix_link = nullptr;
    temp ->output_link = nullptr;
    temp ->pattern_ind = -1;

    return temp;
}

void build_Trie(node* root, vector<string> &patterns){
    for(int i = 0; i < patterns.size() ;i++){ // iterating over patterns
        node* cur = root;
        for(auto c : patterns[i]){ // iterating over characters in pattern[i]
            if(cur ->child.count(c)) // if node corresponding to current character is already present, follow it
                cur = cur ->child[c];
            else{
                node* new_child = add_node(); // if node is not present, add new node to trie
                cur ->child.insert({c, new_child});
                cur = new_child;
            }
        }
        cur ->pattern_ind = i; // marking node as i-th pattern ends here
    }
}

void build_suffix_and_output_links(node* root){
    root ->suffix_link = root; // pointing suffix link of root back to itself

    queue<node*> qu; // taking queue for breadth first search

    for(auto &it : root ->child){
        qu.push(it.second); // pushing nodes directly attached to root
        it.second ->suffix_link = root; // setting suffix link of these nodes back to the root
    }

    while(qu.size()){
        node* cur_state = qu.front();
        qu.pop();

        for(auto &it : cur_state ->child){ // iterating over all child of current node
            char c = it.first;
            node* temp = cur_state ->suffix_link;

            while(temp ->child.count(c) == 0 && temp != root) // finding longest proper suffix
                temp = temp ->suffix_link;

            if(temp ->child.count(c))
                it.second ->suffix_link = temp ->child[c]; // if proper suffix is found
            else it.second ->suffix_link = root; // if proper suffix not found

            qu.push(it.second);
        }

        // setting up output link
        if(cur_state ->suffix_link ->pattern_ind >= 0)
            cur_state ->output_link = cur_state ->suffix_link; 
        else cur_state ->output_link = cur_state ->suffix_link ->output_link;
    }
}

void search_pattern(node* root, string &text, auto &indices){
    node* parent = root;

    for(int i = 0; i < text.length() ;i++){
        char c = text[i];
        if(parent ->child.count(c)){ // if link to character exists follow it
            parent = parent ->child[c];

            if(parent ->pattern_ind >= 0)
                indices[parent ->pattern_ind].push_back(i); // if this node is marked then a pattern ends here

            node* temp = parent ->output_link;
            while(temp != nullptr){ 
                indices[temp ->pattern_ind].push_back(i); // follow all output links to get patterns ending at this position
                temp = temp ->output_link;
            }
        }
        else{
            while(parent != root && parent ->child.count(c) == 0) // follow suffix links till matching suffix or root is found
                parent = parent ->suffix_link;

            if(parent ->child.count(c))
                i--;
        }
    }
}

/*void BFS(node* root){ // utility function to print the automata
    queue<pair<char, node*>> qu;
    cout <<"\n" <<root <<"\n" <<root ->suffix_link <<"\n" <<root ->output_link <<"\n" <<root ->pattern_ind <<"\n\n";

    for(auto &it : root ->child)
        qu.push(it);

    while(qu.size()){
        auto temp = qu.front();
        qu.pop();

        cout <<temp.second <<"\n" <<temp.first <<"\n" <<temp.second ->suffix_link <<"\n" <<temp.second ->output_link <<"\n" <<temp.second ->pattern_ind <<"\n\n";

        for(auto &it : temp.second ->child)
            qu.push(it);
    }
}*/

int main(){
    int k; //Number of patterns
    cin >>k;

    string text; // given string in which pattern is to be searched
    vector<string> patterns(k); // vector or array of patterns

    for(int i = 0; i < k ;i++)
        cin >>patterns[i];

    cin >>text;

    node* root = add_node(); // allocating memory for root node

    build_Trie(root, patterns); // building trie out of patterns

    build_suffix_and_output_links(root); // creating appropriate suffix and output links

    vector<vector<int>> indices(k, vector<int>());
    search_pattern(root, text, indices);

    // BFS(root); to check the structure of created automata

    for(int i = 0; i < k ;i++){
        cout <<"Total occurrences of \"" <<patterns[i] <<"\": " <<indices[i].size();

        if(indices[i].size())cout <<"\nOccurrences: ";

        for(auto &j : indices[i])
            cout <<j - patterns[i].length() + 1 <<" ";
        cout <<"\n\n";
    }

    return 0;
}

It is to be noted that time complexity of this algorithm depends upon the number of matches. So, the time complexity can tend to be quadratic if there are several occurrences like in case of: a, aa, aaa, aaaa .....

Image Source