
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explained the algorithmic approach for Bottom up traversal of Trie.
Table of content
- What is Trie?
- What is bottom-up traversal of Trie?
- Algorithm
- Code approach
- Complexity
What is Trie?
Trie is a special data structure used to store the data(generally, we store strings) in an efficient way. It is similar to Tree. It is an n-ary tree in which each branch consists of n components. It is also known as prefix tree or digital tree. It consists of nodes and edges. It is an Indexed Structure, often used in information retrieval and organistion.
It is used in dictionary (In Store, Remove, Searching), finding prefix strings. It is an ordered data structure.
Structure of Trie data structure
struct trie-node{
trie-node *child[26]; //26 because english have 26 alphabets
//child will have 26 values
bool we; //"we" stands for end of word
};
- "we" will tell whether the alphabet is the end of word or not?
- "we" will have one(1) or True for last alphabet of the word and zero(0) or False for the remaining the alphabets.
- Structure of trie data structure will look like, given below
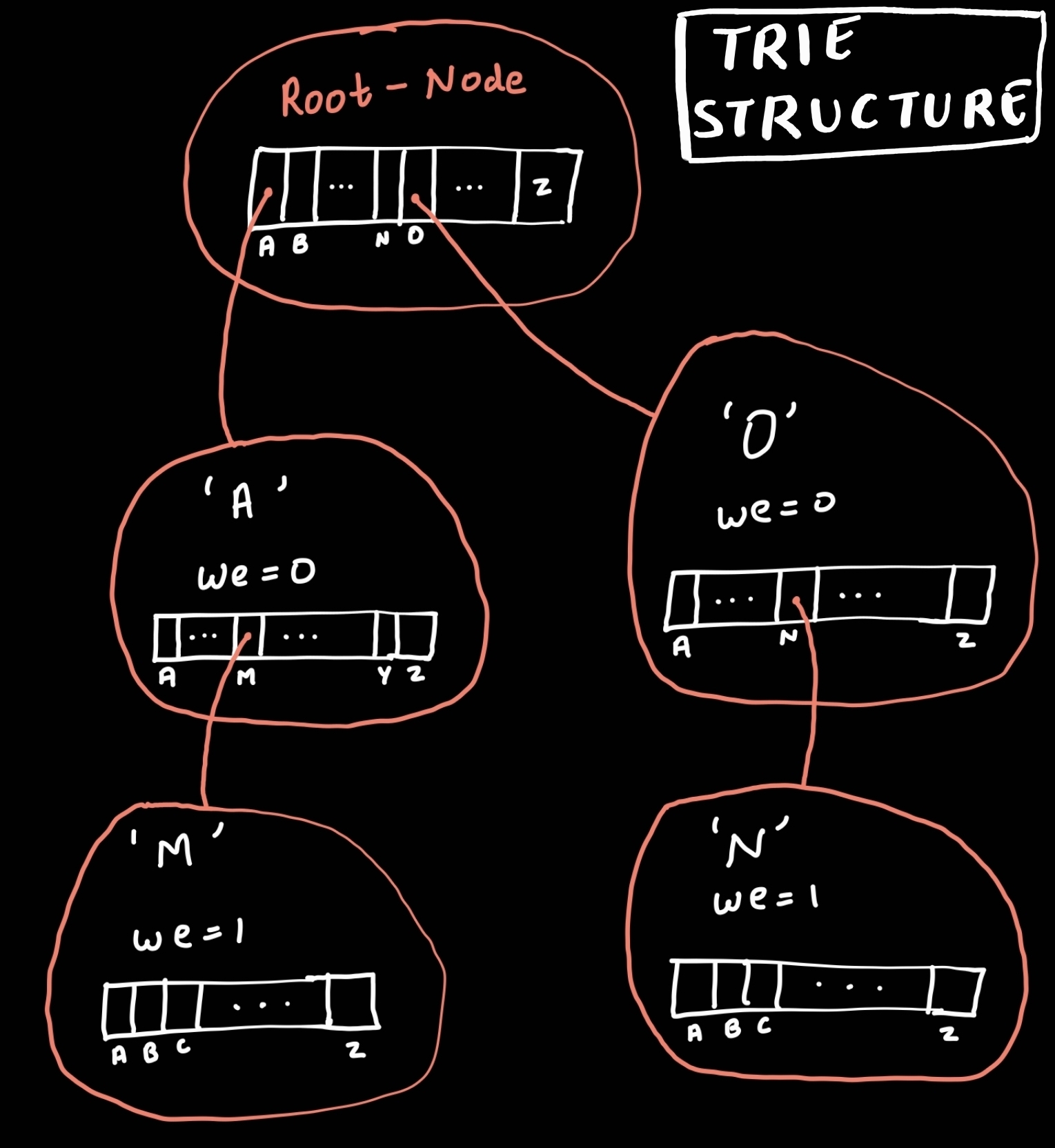
Bottom-up Traversal of a Trie
Bottom-up Traversal of a trie is a way of printing alphabets in bottom to top manner. It is a recursive fuction.
Example: Let's store { cat, coa, bat, bar, on } in Trie. Trie will look like, given below:
Trie:
Root-Node
/ | \
b c o
| / \ |
a a o n
/ \ | |
r t t a
Now, while printing we will first print the left most subtree in bottom-up fashion, then print second left most subtree in bottom-up fashion, then third left most subtree in same manner and soon upto the right most subtree.
In bottom-up, we start printing from bottom alphabet to top alphabet in tree. Therefore, the output will be:
Output: r, t, a, b, t, a, a, o, c, n, o
Bottom-up Traversal of a trie is similar post-order traversal of a tree.
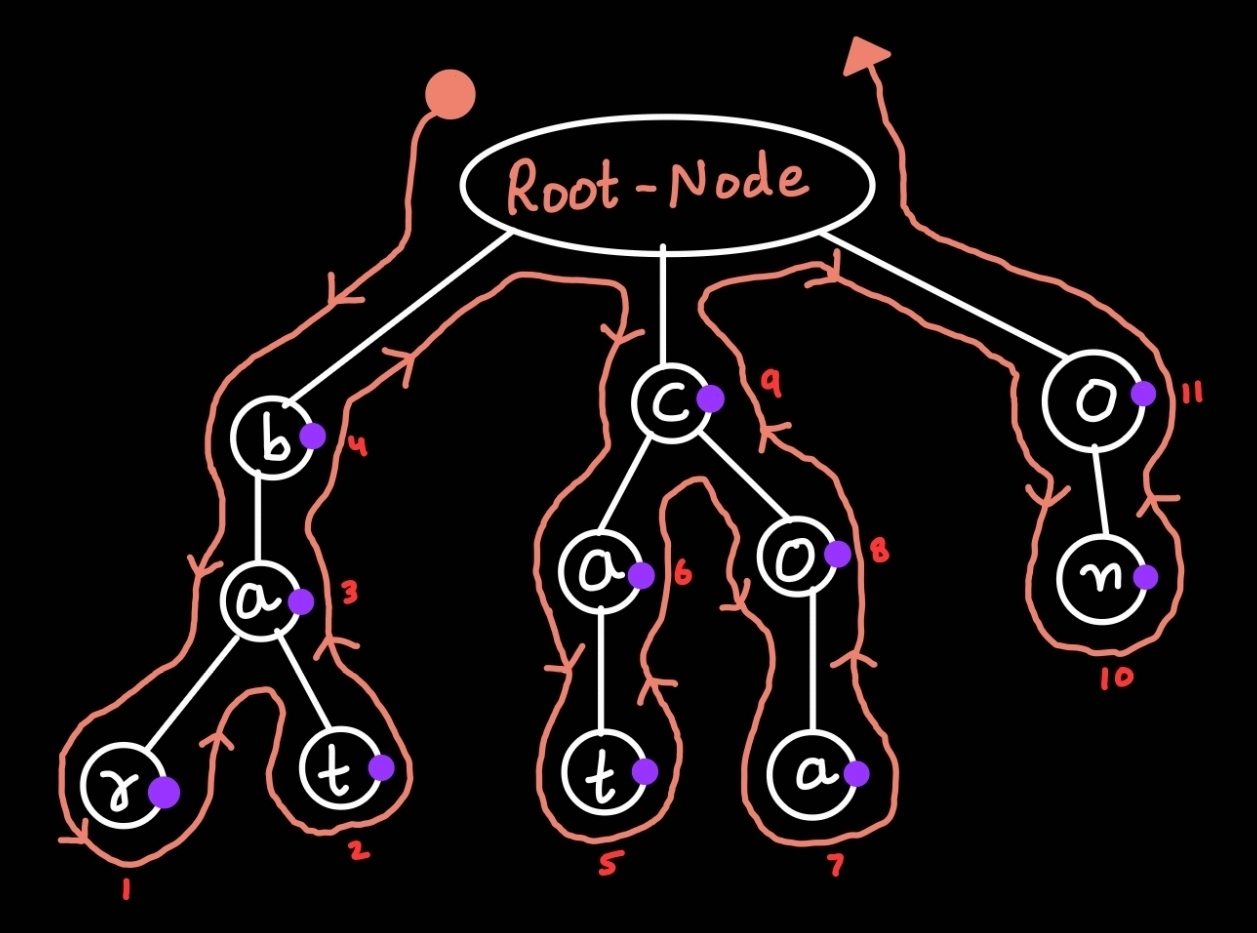
Post-order output of this tree is: { r, t, a, b, t, a, a, o, c, n, o }
Algorithm
Begin B-print:
- We move from top to bottom in recursive fashion.
- If (head is NULL) then return.
- If (head is NOT-NULL) then move to next node(child node) recursively.
- We go down till we don't find the node which contain value of "we = 1" because alphabet in that will be the last alphabet of the word.
- Print the value/alphabet of node when we return.
End B-print.
Code
#include <bits/stdc++.h>
using namespace std;
/*------------Structure of trie-node-------------*/
struct T_node {
bool we;
T_node *child[26];
T_node() //To create new node
{
we = false;
for (int i = 0; i < 26; ++i) {
child[i] = NULL; //Initializing all child value to null
}
}
};
class trie {
public:
T_node *root;
trie() //Constructor
{
root = new T_node();
}
void insert(string ); //Fuction to insert
void b_print(T_node *); //Function to print in Bottom-up manner
};
/*-------------Function to insert the string--------------*/
void trie::insert(string data) {
T_node *head = root; //assigning root to head
int length = data.size(); //length of word
int in= 0; //"in" is for index for child[]
int h = 0; //'h' is for height or level of tree
while (h < length) {
in = data[h] - 'a';
if (head->child[in] == NULL) {
head->child[in] = new T_node();
}
head = head->child[in];
h++;
}
if (head != NULL) {
//assign the "we" true which represent the end of word
head->we = true;
}
}
/*-----------B-print Function to print data--------------*/
void trie::b_print(T_node *head) {
if (head == NULL)
return;
int i = 0;
while (i <= 25) {
if (head->child[i] != NULL && head->we != true) {
b_print(head->child[i]); //Recursive call
cout <<" "<< (char)(i + 97); //To print alphabet
}
i++;
}
}
/*--------------Driver Function--------------*/
int main() {
trie t1; //"t1" is the Object of trie
/*
Root-Node
/ | \
b c o
| / \ |
a a o n
/ \ | |
r t t a
*/
t1.insert("cat");
t1.insert("coa");
t1.insert("bar");
t1.insert("bat");
t1.insert("on");
t1.b_print(t1.root);
return 0;
}
Output: r t a b t a a o c n o
Complexity
Time efficiency depends on the trie data structure and is dependent of the keyword string entered by the user.
Time complexity: O(K), where 'K' is the Total length of the given words(approx). Since, Program will go through each and every node in the trie to print, i.e. like,
If given words are {cat, rat, hat, set}
Length of "cat"= 3
Length of "rat"= 3
Length of "hat"= 3
Length of "set"= 3
then K = (3 + 3 + 3 + 3)
K = 12
Space complexity: O(K), where 'K' represent the number of alphabets in the trie. Since, Program will go to each and every node in trie to print.
