Lexicographic sorting using Trie

Lexicographic sorting is a way of sorting a set of strings based on their alphabetical order We can also say that the order in which those words appear in a dictionary.

Table of contents

• Approach
• Implementation details
• Working
• Output
• Time & space complexity
• Entire code
• Conclusion

Approach

We can divide the approach as following:

• Accept number of words going to be entered
• Insert the word into the trie as we are accepting it
• Iterate through the trie and print the words in order.

Lets look at the approach in detail.

So here we will be using trie to sort these words in lexicographic order. For this first we will store all the words entered by the user in a trie. Then we will traverse through the trie in order and will print the words which we encounter.

To insert a word into the trie we start at the root node and traverse the trie, following the appropriate child node for each letter of the word. If there are no child for a particular letter then we eill create one and make it the child of the current node. Once we reach the end of the word then we will set a bool value to true.

To print the words stored in the trie in a sorted order, we will traverse the trie recursively from the root and then append each letter to the result and when we encounter the bool to be true we will print that word. We do this until we have visited all the nodes in the trie.

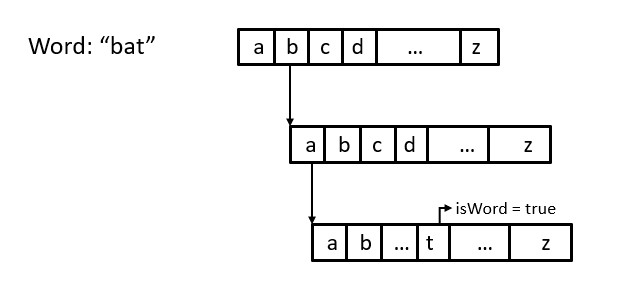
The above image shows how we will be traversing the trie while inserting and printing the word.

Trie is a tree data structure and time complexity to insert n words into the trie is O(n*l) where l is the maximumm length of a word. The time complexity to traverse the trie and to print the words is O(n*l). Since the number of english alphabet is constant, the space complexity of the trie is O(n*l).

Implementation details

• Trie: Trie is a tree-like data structure used for effitient string searchingg and storage. It is also known as a prefix tree, as each of the nodes represent a prefix of one or more strings. This effitient storage and searching property can be useful for applications autocomplete and spell-checking. Checkout the article where I discussed everything on spell-checker. The one disadvantage it has is, it can be memory-intensive, especially when storing large number of long strings but techniques like compression and pruning can be done to reduce the memory usage without sacrificing the performance characteristics.
• struct: struct is a user-defined data type that groups together variables of different data types under a single name. Sounds similar to classes right? Yes but some key differences are there. Unlike classes all memebers in structs can be accessed outside the struct, it can be initialized using the same syntax like an array, and the default accecebility in a struct is public.

Now lets look at the working of the code

Working

So first we will create a struct, which has an array of pointers to its 26 children (26 letters, so one for each) and a boolean flag isWord which will be set to true if a word ends at that node.

truct TrieNode
{
    TrieNode *children[26];
    bool isWord;
}

Now we will create a function which will return us a new node with all its children set to NULL and assign false to the boolean value inside the node. In this function we will first create a new node and then we will iterate through all its childrean and will point it to NULL and give false to the isWord variable.

TrieNode *getNewNode()
{
    TrieNode *node = new TrieNode;
    node->isWord = false;
    for (int i = 0; i < 26; i++)
    {
        node->children[i] = NULL;
    }
    return node;
}

Now we will create an insert function which will insert all the words we enter into the trie using the insert function. In the insert function we will accept root node and the string. First we will initialize a temp node to the root. Then we will iterate through the characters in the string we recieved, and will find the index value by subtracting a from the character then. Now we will check if that index of the node is pointing to NULL or not. If it is then we will create a new node and move the temp to the index of the new node. When that particular word ends we will assign the isWord value to true.

void insert(TrieNode *root, string key)
{
    TrieNode *temp = root;
    for (char c : key)
    {
        int idx = c - 'a';
        if (!temp->children[idx])
        {
            temp->children[idx] = getNewNode();
        }
        temp = temp->children[idx];
    }
    temp->isWord = true;
}

Now we will make the traverse() which will be used to print all the words in order. This function accepts the current node and the string prefix. Inside the function we will iterate through the indexes and will check if an index has a child or not, if not then we will move on to the next index, but if it has a child then we will recursivly call the traverse function and pass it the current node and the current prefix. If a node comes up with isWord is true then we will print the prefix which would be a word. With this function we will be able to print all the words in a lexicographic order.

void traverse(TrieNode *node, string prefix)
{
    if (node->isWord)
    {
        cout << prefix << endl;
    }
    for (int i = 0; i < 26; i++)
    {
        if (node->children[i])
        {
            traverse(node->children[i], prefix + char(i + 'a'));
        }
    }
}

Now we will create the int main(). Here first we will create a root node using the getNewNode() then we will take in the number of words the user will input. Then we will accept the word and pass it to the insert() inside the for loop. After accepting all the words we will call the traverse() which would print all the words in the required order.

int main()
{
    TrieNode *root = getNewNode();
    int n;
    cout << "Enter the number of words: ";
    cin >> n;
    cout << "Enter the words: ";
    for (int i = 0; i < n; i++)
    {
        string s;
        cin >> s;
        insert(root, s);
    }
    cout << "The sorted words are: " << endl;
    traverse(root, "");
    return 0;
}

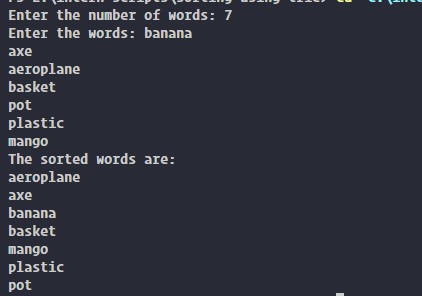
Output

Time & space complexity

Time & space complexity

Here this program implements a trie data structure to store a the collection of words and then to print them ina lexicographic order.

The time complexity of the insert function is O(l), where l is the length of the input string, since we iterate through each character in the string and perform a constant time operation for each character. We do this for each of the n words, so the overall time complexity of building the trie is O(l*n).

The time complexity of the traverse function is O(n*m), where n is the total number of nodes in the trie and m is the maximum number of child nodes of any node in the trie (in this case, m = 26). This is because we visit each node in the trie exactly once and perform a constant-time operation for each child of each node. Since the trie has at most n*l nodes, the overall time complexity of the traverse function is O(n*l) or O(n*l*26).

The space complexity of the insert function is O(l), since we create a new node for each character in the input string, and each node contains a constant number of pointers.

The space complexity of the traverse function is O(l*m*n), (m = 26) since we store the prefix string for each node in the trie, and there are at most n nodes and the length of the prefix string for each node is at most l.

The overall space complexity of the program is O(n*l) or O(n*l*26), since that is the maximum number of nodes that can be created in the trie.

Entire code

The following is the entire code for this operation.

#include <bits/stdc++.h>
using namespace std;

struct TrieNode
{
    TrieNode *children[26];
    bool isWord;
};

TrieNode *getNewNode()
{
    TrieNode *node = new TrieNode;
    node->isWord = false;
    for (int i = 0; i < 26; i++)
    {
        node->children[i] = NULL;
    }
    return node;
}

void insert(TrieNode *root, string key)
{
    TrieNode *temp = root;
    for (char c : key)
    {
        int idx = c - 'a';
        if (!temp->children[idx])
        {
            temp->children[idx] = getNewNode();
        }
        temp = temp->children[idx];
    }
    temp->isWord = true;
}

void traverse(TrieNode *node, string prefix)
{
    if (node->isWord)
    {
        cout << prefix << endl;
    }
    for (int i = 0; i < 26; i++)
    {
        if (node->children[i])
        {
            traverse(node->children[i], prefix + char(i + 'a'));
        }
    }
}

int main()
{
    TrieNode *root = getNewNode();
    int n;
    cout << "Enter the number of words: ";
    cin >> n;
    cout << "Enter the words: ";
    for (int i = 0; i < n; i++)
    {
        string s;
        cin >> s;
        insert(root, s);
    }
    cout << "The sorted words are: " << endl;
    traverse(root, "");
    return 0;
}

Conclusion

With this article at OpenGenus, you must have the complete idea of Lexicographic sorting using Trie.

Here we have discussed the way we can use trie to arrange the words in lexicographic order. This is the same principle which is used in a variety of real world application like spell-checker, auto complete etc.