Introduction

Binary search tree contains nodes with each having maximum of 2 child nodes. Nodes are arranged such that the search operation consumes O(logn). In a BST, value of elements in left subtree are less than root's and value of elements in right subtree are greater than root's; this property shall be valid for any subtree and whole tree itself.

The article tries to explain how a BST can be reconstructed when pre-order traversal of the BST is given in an incremental manner: A version of the method is discussed, and the method is improved to cover another set of different case, code is modified to cover the updated method.

Edition 1

Consider the below binary search tree and corresponding pre-order traversal as in picture

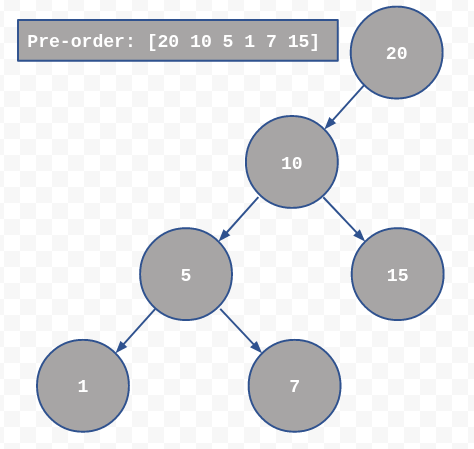
It's clear that the first element is root and the next element is left if it's value is less than current else right child.

root->data = preorder[0], cur = root
for i in preorder array
    if i > cur->data
         then, cur->right = new bst node (i), cur = cur->right
    else
        cur->left = new bst node (i), cur = cur->left

Below tree is the outcome of above algorithm.

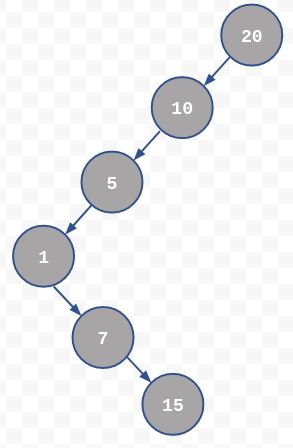
It's clear that the tree produced by this algorithm is not a BST!

Edition 2

We shall somehow reach back to the node whose value is 5 & attach node 7 to it's right & similar case goes for 15 too. One apprach is to remember the node that gets attached as soon as it becomes part of tree. Stack fits fine for this case as accessing tree is done in LIFO manner (last attachned node 5 is accessed before 10 is accessed).

So the algorithm goes something like this,
If peek element in stack is greater than current element in pre-order traverse then the new element can be directly attached to peek's left as below

if top(stack)->data > preorder[i]
    top(stack)->left = new bst node (i)

but, if the pre-order element is greater than peek, then element needs to be attached to rght side. For a given node in BST all/any element/s in left subtree are lesser than the node itself & right subtree element/s are greater. Consider 15 in the actual BST, it can't be in left subtree of the node 10. So the right element of a node is greater than node & is less than node's parent.
Keep popping stack till the top of stack is less than pre-order element. Attach the element as right child of last pop node & also push the newly attached node into stack.

Step-by-step algorithm:

1. Input pre-order traversal of the BST
2. Initialise a BST with root's data having first element of the input array
3. Initialise a stack which can hold a BST node & push the above element
4. Initialise an index variable say i with 1
5. Read i'th value from preorder array into data
6. if data is greater than top element in stack then
7. pop elements from stack into say temp till stack is not empty or till data is greater than top
8. Create a BST node with data as it's data and attach it to temp's right and push temp's right to stack
9. if the condition in step 6 failed to be true then,
10. Create a BST node with data as it's data and attach it to top's left and push the newly created BST node to stack
11. increment i and goto repeat from step 5 till i becomes invalid

C code

#include <stdio.h>
#include <stdlib.h>

struct _bst {
	int data;
	struct _bst *left, *right;
};
typedef struct _bst bst_t;

struct _stack {
	bst_t *data;
	struct _stack *next;
};
typedef struct _stack stack_t;

stack_t* push(stack_t *s, bst_t *data) {
	stack_t *t;

	t = malloc(sizeof(*t));
	t->next = s;
	t->data = data;
	return t;
}

stack_t* pop(stack_t *s, bst_t **data) {
	stack_t *t = NULL;
	if (s) {
		t = s->next;
		if (data) *data = s->data;
		free(s);
	}
	else
		if (data) *data = NULL;
	return t;
}

bst_t* top(stack_t *s) {
	return (s) ? s->data : NULL;
}

// it does not need to be function at all
// you may inline if you really want a seperate
// function for this;
#define isempty(s) ((s) == NULL)

bst_t* preorder_to_bst(int *preorder, unsigned int n) {
	bst_t *root = NULL, *temp = NULL, *cur = NULL;
	stack_t *s = NULL;
	int i, data;

	// step 2
	root = malloc(sizeof(*root));
	root->data = preorder[0], root->left = root->right = NULL;

	// step 3
	s = push(s, root);

	// step 4-11
	for (i = 1; i < n; ++i) {
		// step 5
		data = preorder[i];
		// step 6
		if (data > top(s)->data) {
			// step 7
			while (!isempty(s) && data > top(s)->data) {
				s = pop(s, &temp);
			}
			// step 8
			temp->right = malloc(sizeof(*temp->right));
			temp->right->data = data, temp->right->left = temp->right->right = NULL;
			s = push(s, temp->right);
		}
		else
			// step 9
			if (data < top(s)->data) {
				// step 10
				top(s)->left = malloc(sizeof(bst_t));
				top(s)->left->data = data,
					top(s)->left->right = top(s)->left->left = NULL;
				s = push(s, top(s)->left);
			}
	}

	return root;
}

// inorder traversal of the given BST is displayed
void bst_inorder(bst_t *root) {
	if (root) {
		bst_inorder(root->left);
		printf("%d ", root->data);
		bst_inorder(root->right);
	}
}

int main() {
	// let the below array be output of preorder traversal
	// of a valid BST
	int preorder[] = {20, 10, 5, 1, 7, 15, 30, 25, 32, 40};
	unsigned int n = sizeof(preorder) / sizeof(preorder[0]);

	// get root for the reconstructed BST
	bst_t *root = preorder_to_bst(preorder, n);

	// validate answer by displaying corresponding
	// BST's inorder traversal
	bst_inorder(root);
	puts("");
	return 0;
}

Notes: The above code tries to explain the concept, but some of the basic validations are not included in the code such as,

• Validation of malloced memory
• Memory freeing post it's usage
• NULL pointer validation of function arguments

Applications

• Storing data in a data-structure helps process it easily depending on type of processing. Let's say system would need to access tree after the process is restarted, in that case tree data might need to be written to a file. Tree data might need to be written sequentially using a traversal mechanism. When data needs to be represented in tree format again, method discussed in this article might be used.
• There may be a need of transferring tree to other processes or even over network. In these cases, data is transmitted sequentially either via pipes or via sockets. Tree can be reconstructed on receiving end with the method discussed in this article efficiently as it uses no recursion.

Complexity

• Time complexity of the algorithm is O(n²).
• Space complexity of the algorithm is O(2n) - If there are n elements in the input array then, n amount of space might be consumed by stack and another n amount of space will be consumed by the tree itself.

Readers are encouraged to improve the code and may be even the algorithm itself. One possible & simple improvement to the code would be to input array via command-line arguments, stdin, files and providing choice of selecting any of the method. To validate your improvements, please rebuild the input from a valid BST and never interchange array elements.

With this article at OpenGenus, you must have the complete idea of constructing Binary Search Tree (BST) from a given pre-order traversal. Enjoy.