
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Inverting a binary tree (or reversing) is one of the most common questions asked in the interviews of many companies. In this article, we will see in detail as to how one can understand and tackle this task of inverting a binary tree using recursion, stack and queue.
Table of Contents:
- Binary tree
- Inversion of a binary tree
- Methods of Inversion
- Recursion
- Iterative solution using stack
- Iterative solution using queue
- Time and space complexities of different solutions
Binary Tree
When every non-leaf node in a tree has atmost 2 children, its called a binary tree. Given below is an example of a binary tree.
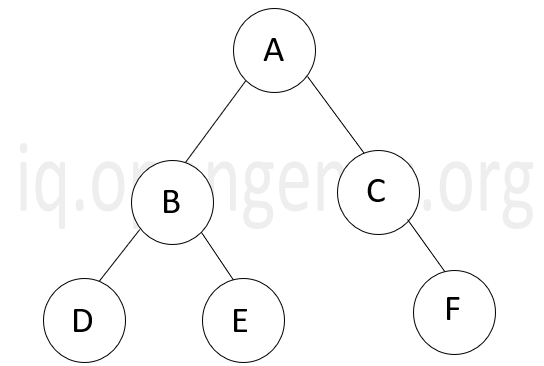
Inversion of a Binary tree
Inverting a binary tree is producing another binary tree as output where all the left and right nodes of all non-leaf nodes of the original binary tree are interchanged. The inverted binary tree is also known as a Mirror tree. For example:
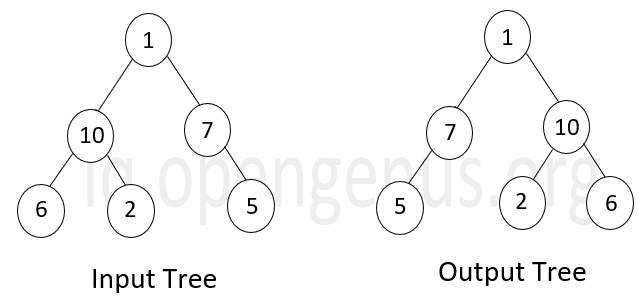
Methods of inversion
A binary tree can be inverted using either recursion or iteration. For both cases, the basic code for the binary tree node is as follows:
class Node:
def __init__(self,val=0):
self.data=val
self.left=None
self.right=None
Recursion
In this method, we invert the given binary tree by swapping the left and right nodes and recursively carrying out the same process for each non-leaf node until we reach the leaf node.
Steps to invert a Binary Tree:
- If root/ current node is NULL, inverting is done.
- For current node N, swap left and right child nodes.
- Process new left and right child with step 1 and 2 recursively.
Code snippet:
Following is the code to invert a Binary Tree recursively:
class Inversion:
def invert(self,root:Node):
if root == None:
return None
//Swapping the children
temp = root.left
root.left = root.right
root.right = temp
//Recursion
self.invert(root.left)
self.invert(root.right)
return root
Explanation:
In the above code snippet, the invert function first checks whether the tree is empty. If not, it first swaps the two children of the root and the recursively swaps the two sub-trees until the the root has some value. Once the root is NULL, the recursive calls are stopped.
Iterative solution using stack
This method is similar to the preorder traversal . The given binary tree is inverted using a stack created where the roots are stored and inversion is carried out using the stack operations.
Steps to invert a Binary Tree iteratively using Stack:
- If root/ current node is NULL, inverting is done.
- Define a stack S.
- Add root node to stack S.
- While stack S is not empty:
4.1. Pop node N from stack S
4.2. Swap left and right child of node N
4.3. Push new left and right child of node N to stack S. - The Binary Tree is inverted.
Code snippet:
class Inversion:
def swap(root):
if root == None:
return
//Swapping the children
temp = root.left
root.left = root.right
root.right = temp
def invert(root:Node):
if root == None:
return
stack = []
stack.append(root)
while (stack.empty()!=True):
current = stack.pop()
swap(current)
if(current.right):
stack.append(current.right)
if(current.left):
stack.append(current.left)
Explanation: In the above code snippet,the class Inversion contains two functions: a swap function to swap the left and right children of the root and an invert function to perform the inversion.
In the invert function, a stack is created and the root is pushed into it at first. Then the top element of the stack is popped and is sent through the swap function and the resultant right and left nodes are pushed into the stack in the same order. This is repeated till the stack is empty.
Iterative solution using queue
In this method, the code is similar to level order traversal. A queue is created instead of a stack which stores the roots and the inversion is performed in an orderly manner. For performing queue operations, the queue module is imported as follows:
from queue import Queue
Steps to invert a Binary Tree iteratively using Queue:
- If root/ current node is NULL, inverting is done.
- Define a queue Q.
- Add root node to queue Q.
- While queue Q is not empty:
4.1. Pop node N from queue Q from left side.
4.2. Swap left and right child of node N
4.3. Push new left and right child of node N to queue Q. - The Binary Tree is inverted.
Code snippet:
class Inversion:
def swap(root):
if root == None:
return
//Swapping the children
temp = root.left
root.left = root.right
root.right = temp
def invert(root:Node):
if root == None:
return
q = Queue()
q.put(root)
while(q.empty()!=True):
current = q.popleft()
swap(current)
if current.left:
q.put(current.left)
if current.right:
q.put(current.right)
Explanation: In the above cone snippet too, the class Inversion contains a swap function and an invert function which is for the same purpose as the ones given in
' Iterative solution using stack ' even though both the invert functions differ logically.
In the invert function, a queue is created and the root is added to it at first. Then the left most element i.e. front node of the queue is dequeued and sent through the swap function to swap its left and right children. First, the left child of the popped node is enqueued followed by the right child. This is repeated until the queue is empty.
Time and space complexities different soutions
The time complexity and space complexity for different solutions are given below.
| Method | Time Complexity | Space Complexity |
|---|---|---|
| Recursion | O(n) | O(h) |
| Iterative solution using stack | O(n) | O(n) |
| Iterative solution using queue | O(n) | O(n) |
In the above table, n is the total number of nodes in the tree and h is the height of the tree.
When the iterative methods of inverting a binary tree are considered, in cases of both stack and queue, the addition and deletion operation takes place only once for every node present in the tree. Therefore, the total number of operations perfomed = 2n. And since each node is visited only once, the time complexity is O(n) in both cases. We notice that in both these cases, memory space is occupied only by the stack or queue created whose maximum number of elements can be n (Worst case scenario). So, the space complexity is O(n) for both the cases.
When the recursive method of inverting a binary tree is considered, the time complexity is O(n) as each node of the tree is traversed only once. Since there is recursion, function calls are stored in an auxillary recursion stack. It is to be noted that that the recursive function is called for every level and the worst case scenario is when the function calls of all levels are placed in the auxillary stack. Therefore if h is the height of the binary tree, the space complexity in this case will be O(h).
Upon completion of this article at OpenGenus, you must have a clear understanding on how to invert a binary tree.
