
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we discuss how to delete the middle element of a queue without using other data structures. We have explained both iterative and recursive approach.
Table of contents:
- Introduction to Queue
- Problem statement: Delete the middle element from queue
- Iterative Approach
- Recursive Approach
- Time and Space Complexity Analysis
Pre-requisites:
Introduction to Queue
A queue is an abstract linear data structure that stores elements in a sequential order.
It uses FIFO(first in first out) approach for accessing elements.
Picture a line of people in a bank, all waiting to get served by the teller. A new person joins the queue from the end and the first person on the queue would be leaving the queue.(first come first serve).

Common types of queues.
1. Simple queue.
Just like we have described above, insertions and deletions take place in the back and front respectively.
Applications include; process scheduling, I/O buffer, disk scheduling.
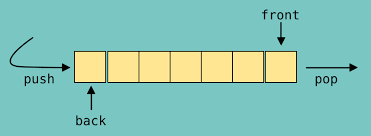
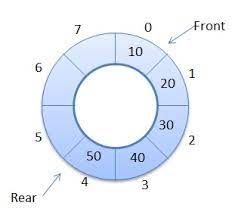
2. Circular queue.
The first node is connected to the last node, also known as a ring buffer.
Insertions take place at the front and deletions at the end of the queue.
Applications include; memory management, CPU-scheduling, computer controlled traffic systems.
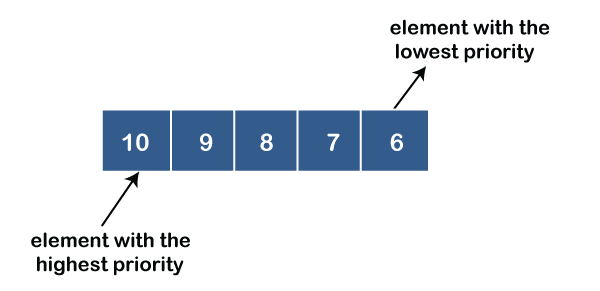
3. Priority queue.
Nodes in the queue have an assigned priority therefore a node with the highest/lowest priority will be the first to be removed.
They can be asceding or descending priority queues.
Applications include; CPU-scheduling algorithms, prims algorithm, heap sort.
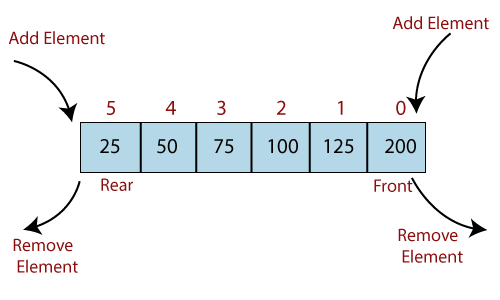
4. Doubly ended queues(dequeue) 'deck'.
Insertions and deletions take place at both the front and ends of the queue.
Applications include; saving browser history, stack implementation.
Queue operations
- enqueue(): add element to end of queue.
- dequeue(): removing an element from the front of the queue.
- peek()/front(): returns the element at the front of the queue.
- rear(): returns the last element of the queue.
- isFull(): returns boolean true or false based on capacity of queue.
- isEmpty(): returns boolean true if queue is empty, false otherwise.
Problem statement: Delete the middle element from queue
Example:
Input: queue[] = [1, 2, 3, 4, 5], n = 5, mid = 3.
Output: [1, 2, 4, 5]
Explanation
The queue size is an odd number, therefore the middle element is 3.
Input: queue[] = [1, 2, 3, 4, 5, 6, 7, 8], n = 8, mid = 4.
Output: [1, 2, 3, 5, 6, 7, 8]
Explanation
The queue size is an even number thus we have two elements in the middle that is 4 and 5, we remove the first to appear.
Iterative Approach
We initialize a curr variable to store the current position in the iteration, while curr is not equal to size of the queue we pop elements from the queue and push them back except the case where curr is the middle element.
Steps:
- Initialize curr variable to store current position.
- Loop through the queue while it has elements and pop all elements, store front element before popping it from queue.
- Push the elements popped to the queue excluding the mid element (queue-size / 2).
- The queue now has all its previous elements excluding the mid element.
Code
#include<iostream>
#include<queue>
using std::queue;
using std::cout;
using std::endl;
class RemoveMid{
public:
//iterative approach
void removeMidIter(queue<int> &q){
int n = q.size(), curr = 0;
int x = ((n % 2) == 0) ? (n/2-1) : (n/2);
//pop from main queue and push to temp queue except where curr = n/2
while(curr != n){
int i = q.front();
q.pop();
if(curr != x){
q.push(i);
}
curr += 1;
}
}
//helper to print queue
void printQueue(queue<int> q){
while(!q.empty()){
int s = q.front();
q.pop();
cout << s << " ";
}
cout << endl;
}
};
int main(){
RemoveMid rm;
queue<int> q;
for(int i = 1; i <= 7; i++)
q.push(i);
rm.printQueue(q);
rm.removeMidIter(q);
rm.printQueue(q);
return 0;
}
Recursive Approach
We use a recursive approach whereby we pop elements from the queue and push them back to the queue this time skipping the middle element.
The algorithm terminates when the base case(empty queue) is triggered.
Steps:
- Initialize current variable to store the current position.
- Store the front element of queue in a variable then pop the queue.
- Check the condition of mid element if curr is not equal to mid, push the front element to the queue
- Recursively repeat the above steps, the recursion will stop when the queue is empty or curr is equal to queue size.
- Finally we have a queue without the middle element.
Code
#include<iostream>
#include<queue>
using std::queue;
using std::cout;
using std::endl;
class RemoveMid{
public:
//recursive approach
void removeMidRec(queue<int> &q, int n, int curr = 0){
//base case (queue is empty, all elements popped)
if(q.empty() || curr == n)
return;
//if queue size is even remove the first mid element else remove mid element
int x = ((n % 2) == 0) ? (n/2-1) : (n/2);
//remove from front element
int i = q.front();
q.pop();
//add elements back to front of queue except mid element
if(curr != x)
q.push(i);
removeMidRec(q, n, curr + 1);
}
//helper to print queue
void printQueue(queue<int> q){
while(!q.empty()){
int s = q.front();
q.pop();
cout << s << " ";
}
cout << endl;
}
};
int main(){
RemoveMid rm;
queue<int> q;
for(int i = 1; i <= 7; i++)
q.push(i);
rm.printQueue(q);
//rm.removeMidRec(q, q.size());
rm.removeMidIter(q);
rm.printQueue(q);
return 0;
}
Output
1 2 3 4 5 6 7
1 2 3 5 6 7
what happens
Given the queue q = [1, 2, 3, 4, 5]
Recursive calls:
1st call: curr = 0, x = 1, queue = [2, 3, 4, 5, 1]
2nd call: curr = 1, x = 2, queue = [3, 4, 5, 1, 2]
3rd call: curr = 2, x = 3, queue = [4, 5, 1, 2], curr == to mid, so we don't push to queue
4th call: curr = 3, x = 4, queue = [5, 1, 2, 4]
5th call: curr = 4, x = 5, queue = [1, 2, 4, 5]
queue is empty, base case is triggered, algorithm terminates.
Time and Space Complexity Analysis
All queue operations take constant time and traversing the queue of size n takes O(n) time complexity.
We need no extra space, we use the same queue therefore this makes the space complexity constant O(1).
Questions:
- Can you think of another approach to solve this problem?
- Implement a queue using stacks and a stack using queue.
