
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
Fenwick Tree / Binary indexed tree (BIT) is a data structure used to process interval/range based queries. Compared to segment tree data structure, Fenwick tree uses less space and is simpler to implement.
One disadvantage of Fenwick tree is that it can be only used with an operation that is invertible. For example,
Addition is an invertible operation:
if a + b = c
then c - a = b (where - acts as inverse of addition)
Maximum is a non-invertible operation:
given max(a, b) = c
We don't have any inverse operation to get back a or b.
Although Fenwick tree is generally used for storing dynamic cumulative frequency tables, it can be used with any operation that satisfies above criterion. Fenwick tree allows processing range queries and updates in logarithmic time and thus, it must be used where several such queries are to be processed.
And important operation in implementation of Fenwick tree is finding position of least significant one. Considering 2-complement form of negative numbers, we can perform bitwise and to get position of least significant one:
int LSB(int i){
return i & (-i);
}
for example:
LSB(12) = 001100 & (-001100)
= 001100 & 110100
= 000100
Fenwick tree is typically implemented as an array and is indexed using bits of integer keys. These integer keys fall in range [1...n], skipping 0.
Let ft[] be the array representing Fenwick tree. Then the element ft[i] is responsible for the range [(i - LSB(i) + 1) ... i].
This feature is used to build up the Fenwick tree and so it can be seen that Fenwick tree is a multi-way tree.
The basic idea behind Fenwick tree is that since any integer can be represented as sum of powers of 2, we can represent cumulative frequencies as sum of non-overlapping sub-frequencies.
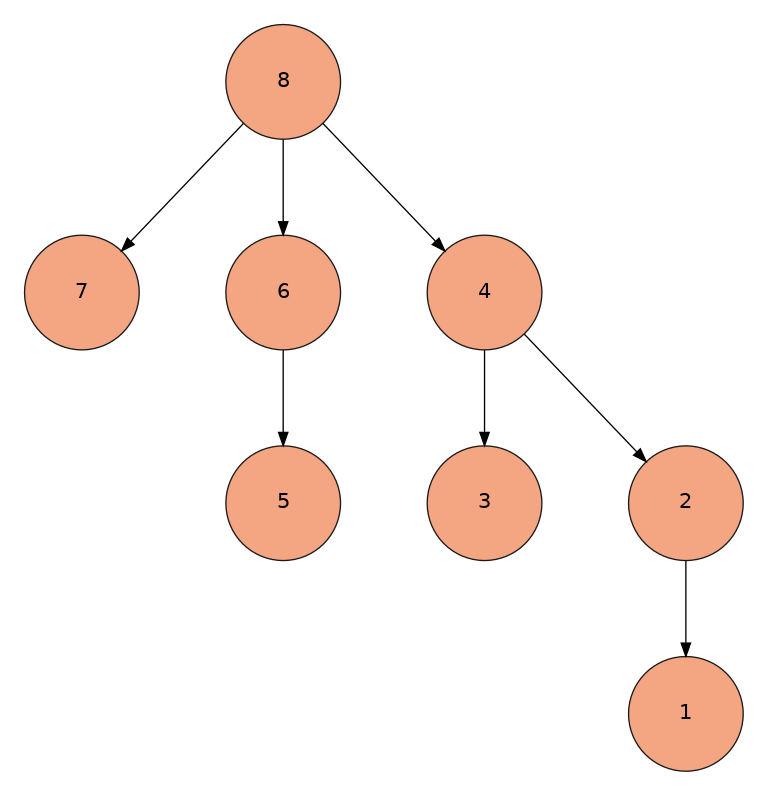
Above diagram shows responsibility of each indices from 1 to 8 where each node is responsible for its own index in array and that of its children. Suppose ft[] is Fenwick tree and ar[] is the original array, then:
ft[1] is responsible for ar[1 - LSB(1) + 1 ... 1]
i.e. ar[1 ... 1] or just ar[1]
.
.
ft[4] is responsible for ar[4 - LSB(4) + 1 ... 4]
i.e. ar[4 - 4 + 1 ... 4]
ar[1 ... 4]
or ar[1, 2, 3, 4]
ft[5] is responsible for ar[5 - LSB(5) + 1 ... 5]
i.e. ar[5 - 1 + 1 ... 5]
ar[5 ... 5]
ar[5]
.
.
ft[8] is responsible for ar[8 - LSB(8) + 1 ... 4]
i.e. ar[8 - 8 + 1 ... 4]
ar[1 ... 8]
or ar[1, 2, 3 ... 7, 8]
So ft[8] will give sum of range 1 to 8, ft[5] is just element ar[5] and so on.
To query a range 1 to b:
let b' = b - LSB(b)
then query(1 ... b) = ft[b] + ft[b'] + ft[b''] + ... ft[1]
It has to be noted that:
- Adding LSB(x) to x allows it to traverse its responsibility tree upwards.
- Subtracting LSB(x) from x gives the largest index that is not responsibility of x.
Pseudocode
Below is pseudocode for a Fenwick tree that returns interval sum.
- array[] is the array upon which Fenwick tree is to be built with length n.
- ft[] is the Fenwick tree. It is a 1-indexed array of length n.
- Least significant bit operation :
function LSB(i): return i & (-i)&isbitwise and. - Querying an interval : This uses 2 functions. One function returns sum for interval [1, x] while second function calls the first function to return sum for interval [start, end].
function query(x): sum = 0 while x > 0: # Process appropriately sum = sum + ft[x] x = x - LSB(x) return sum function Query(start, end): return query(end) - query(start - 1) - Updating array at index x : Fenwick tree doesn't use any build function. Rather, it is considered that the tree is built from an array of length n with all elements 0. Update operation has to be used to insert every element of array[] into ft[] one by one.
function update(pos, value): while pos <= n: ft[pos] = ft[pos] + val pos = pos + LSB(pos)
Complexity
Space complexity : O(n)
Worst case time complexities:
- Update : O(log2(n))
- Query : O(log2(n))
Where n is the length of array.
Implementations
C++ 11
#include <iostream>
#include <vector>
class FenwickTree{
private:
std::vector<int> ft;
public:
// Function to get least significant bit
int LSB(int x){
return x & (-x);
}
int query(int x){
int sum = 0;
while(x > 0){
sum = sum + ft[x];
x = x - LSB(x);
}
return sum;
}
int query(int start, int end){
return query(end) - query(start - 1);
}
void update(int pos, int value){
// array[pos] += value
while(pos <= ft.size()){
ft[pos] += value;
pos = pos + LSB(pos);
}
}
FenwickTree(std::vector<int> array){
int n = array.size();
// Initialize array ft
ft.assign(n + 1, 0);
for(int i = 0; i < n; ++i){
update(i + 1, array[i]);
}
}
};
int main(){
//sample code
std::vector<int> array = {1, 2, 3, 4, 5, 6};
FenwickTree ft(array);
std::cout << "Array is\n";
for(int i = 0; i < 6; ++i)
std::cout << array[i] << ' ';
std::cout << '\n';
std::cout << "Sum of interval [1, 4] is " << ft.query(1, 4) << '\n';
std::cout << "After changing 3 to 10, array is\n";
array[3 - 1] += 7;
ft.update(3, 7);
for(int i = 0; i < 6; ++i)
std::cout << array[i] << ' ';
std::cout << '\n';
std::cout << "Sum of interval [1, 4] is " << ft.query(1, 4) << '\n';
return 0;
}Applications
- Is much more space efficient than the Segment tree.
- The queries can be processed in O(log2n) time.
- Used for finding range sum/product, prefix sum/product etc.
- Cannot be used for range min/max.
