Segment Tree

Reading time: 30 minutes | Coding time: 12 minutes

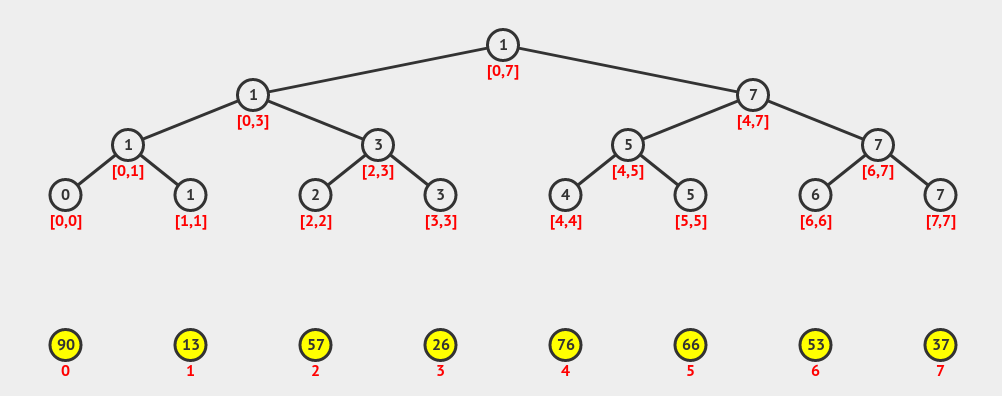
The image above shows structure of a segment tree used to store index of minimum element in the respective intervals of array. The root, as can be seen above, represents the complete array, while its left child represent the left half of array and right child represents the right half, and its same for their children.
Since the leaves represent just one element of array, they store the information about that single element. The internal nodes merge the information from its children nodes, which is in the above diagram, done by comparing the 2 elements stored by its children and storing the index of smaller element. The process of merging depends entirely on the type of information being stores, for example, a segment tree that stores sum of elements in a segment just adds the value stored in left and right children and stores it in parent node.

It is obvious the the height of segment tree ceil(log₂n) where n is length of the array. is A segment tree is expected to perform two primary operations both in logarithmic time:

1. Query : Return the information about some segment or interval.
2. Update : Update value of an element and reflect changes in tree accordingly.

Pseudocode

• Structure of node : A node stores atleast the following
  1. Interval represented by the node.
  2. Information of the interval represented.
  3. Left child.
  4. Right Child.
• Construction of segment tree from the linear array (recursive function) :

    function build(current_node, L, R):
        current_node.interval = (L, R)
        # if leaf node
        if L == R:
            current_node.value = array[L]
            return
        current_node.left = new node
        current_node.right = new node
        # left node represents first half
        build(current_node.left, L, (L + R)/2)
        # right node represents right half
        build(current_node.right, (L + R)/2 + 1, R)
        current_node.value = merge(current_node.left, current_node.right)
        return
    
    n = length of array
    build(root, 0, n - 1)

Above algorithm assumes array to be 0-indexed.
The function merge is written based on type of information to be stored.
For a segment tree that stores minimum element of a segment, merge would be like:

function merge(left_node, right_node):
        if left_node.value < right_node.value:
            return left_node.value
        return right_node.value

Meanwhile for a segment tree that stores sum of elements in an interval, merge would be:

    function merge(left_node, right_node):
        return left_node.value + right_node.value

• Querying an interval (start, end) :

    function query(current_node, start, end):
        (L, R) = current_node.interval
        # if requested range outside interval represented by node
        if R < start or L > end:
            return None
        # if node interval completely inside requested range
        if start <= L and end >= R:
            return current_node.value
        
        # otherwise, recursively go deeper
        left_value = query(current_node.left, start, end)
        right_value = query(current_node.right, start, end)
        # merge is modified to handle None values
        return merge(left_value, right_value)

• Updating array at index x :
  Below pseudocode updates array to a new value.

    function update(current_node, int x, new_value):
        (L, R) = current_node.interval
        # if current node is target leaf node
        if L == R:
            current_node.value = new_value
            # update array
            array[L] = new_value
            return
        
        # if target index within left half node interval, update left child
        if L <= x and (L + R)/2 => x:
            update(current_node.left, x, new_value)
        # if target node in right child
        else:
            update(current_node.right, x, new_value) 
        # merge updated children nodes to update parent node
        merge(current_node.left, current_node.right)        

Complexity

Space complexity : O(2 * n - 1)
Worst case time complexities

• Build : O(1) + O(2) + O(4) ... O(2^{ceil(log₂n)}) = O(2 * n - 1))
• Update : O(log₂(n))
• Query : O(log₂(n))
  Where n is the length of array.

Implementations

Code in C++ 11:

/*
Min Segment Tree : Processes "the minimum element in interval/range" query
*/

#include <iostream>
#include <utility>
#include <vector>

struct Node{
    // store the index of minimum element in interval
    int min_index;
    // store the interval in a pair of integers
    std::pair<int, int> interval;
    Node *left;
    Node *right;
};


/* merge fucntion compares the two indices and return the index which
   has the smallest element. */
int merge(std::vector<int> array, int i, int j){
    // Hnadle NULL cases. If bith NULL, just return NULL
    if(i == -1)
        return j;
    if(j == -1)
        return i;

    if(array[i] < array[j])
        return i;
    else
        return j;
}

void build(std::vector<int> array, Node *cur_node, int L, int R){
    cur_node->interval = std::make_pair(L, R);
    if(L == R){
        // if current node is a leaf node
        cur_node->min_index = L;
        return;
    }
    cur_node->left = new Node;
    cur_node->right = new Node;

    build(array, cur_node->left, L, (L + R) / 2);
    build(array, cur_node->right, (L + R) / 2 + 1, R);

    cur_node->min_index = merge(array, cur_node->left->min_index,
                                cur_node->right->min_index);
    return;
}

// returns the index of smallet element in the range [start, end]
int query(std::vector<int> array, Node *cur_node, int start, int end){
    if(start > end)
        return -1;
    int L = cur_node->interval.first;
    int R = cur_node->interval.second;

    if(R < start || L > end){
        // -1 used here as NULL
        return -1;
    }

    if(start <= L && end >= R){
        return cur_node->min_index;
    }

    int left_index = query(array, cur_node->left, start, end);
    int right_index = query(array, cur_node->right, start, end);

    return merge(array, left_index, right_index);
}

// update adds new value to array[x] rather than replace it
void update(std::vector<int> &array, Node *cur_node, int x, int value){
    int L = cur_node->interval.first;
    int R = cur_node->interval.second;

    if(L == R){
        array[L] += value;
        // since node actually stores the index, no need to change value in
        // leaf node
        return;
    }

    if(L <= x && (L + R)/2 >= x){
        // x is in left subtree
        update(array, cur_node->left, x, value);
    }
    else{
        // x is in right subtree
        update(array, cur_node->right, x, value);
    }

    //update current node
    cur_node->min_index = merge(array, cur_node->left->min_index,
                                cur_node->right->min_index);
}

// To clear allocated memory at end of program
void clearMem(Node *cur_node){
    int L = cur_node->interval.first;
    int R = cur_node->interval.second;

    if(L != R){
        clearMem(cur_node->left);
        clearMem(cur_node->right);
    }
    delete cur_node;
}


int main(){
    // define n and array
    int n = 8;
    std::vector<int> array = {5, 4, 3, 2, 1, 0, 7, 0};

    Node *root = new Node;
    build(array, root, 0, n - 1);

    // sample query
    std::cout << "The smallest element in the interval [1, 6] is "
              << array[query(array, root, 0, 5)] << '\n';

    // change 0 at index 5 to 8
    update(array, root, 5, 8);

    std::cout << "The smallest element in the interval [1, 6] after update is "
              << array[query(array, root, 0, 5)] << '\n';

    clearMem(root);
    return 0;
}

Applications

• Segment tree allows segments to be stored in an arbitrary manner.
• The queries can be processed in O(log₂n) time.
• Used for finding range sum/product, range max/min, prefix sum/product etc.

References/ Further reading

• Wikipedia page on segment trees. Also look up the ppt presentation cited as source.
• Steven Halim's website for visualizing algorithms. Figure used above is a screen-shot from this website. Extremely helpful for beginners.
• Lazy Propagation allow range updates in O(log₂n) time as opposed to O(log₂n) point updates in classic segment tree.
• Persistent segment tree allows keeping history of updates which is used for advanced applications like k^th smallest element in an interval.