Fibonacci Heap

Reading time: 35 minutes

A Fibonacci heap is a heap data structure similar to the binomial heap. It uses Fibonacci numbers and also used to implement the priority queue element in Dijkstra’s shortest path algorithm which reduces the time complexity from O(m log n) to O(m + n log n), giving the algorithm a huge boost in terms of running time.

Structure

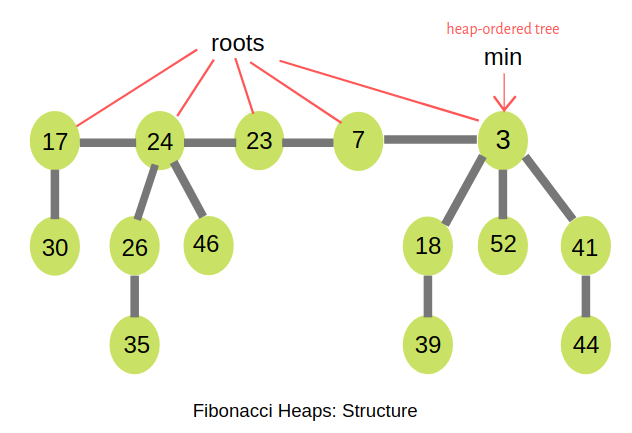
A Fibonacci heap is a collection of rooted trees that are min-heap ordered. That is, each tree obeys the min-heap property: the key of a node is greater than or equal to the key of its parent. Fibonacci heaps are similar to binomial heaps but Fibonacci heaps have a less rigid structure. Each tree has an order just like the binomial heap that is based on the number of children. Nodes within a Fibonacci heap can be removed from their tree without restructuring them, so the order does not necessarily indicate the maximum height of the tree or number of nodes it contains.
An example of Fibonacci Heap consisting of five min-heap-ordered trees and 14 nodes. The minimum node of the heap is the node containing the key 3.

Marked Nodes

An important part of the Fibonacci Heap is how it marks nodes within the trees. The decrease key operation marks a node when its child is cut from a tree, this allows it to track some history about each node. Essentially the marking of nodes allows us to track whether:

• The node has had no children cut (unmarked)
• The node has had a single child cut (marked)
• The node is about to have a second child cut (removing a child of a marked node)

When a second child is cut from its parent, the parent is moved to the root list. This ensures that the structure of the Fibonacci heap does not stray too far from that of the binomial heap, which is one of the properties that enables the data structure to achieve its amortised time bounds.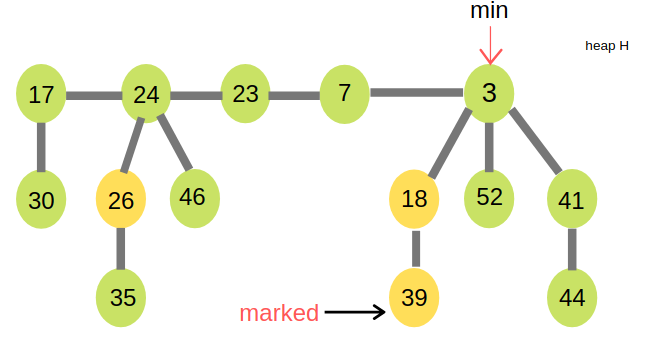

Notation

• n = number of nodes in heap.
• rank(x) = number of children of node x.
• rank(H) = max rank of any node in heap H.
• trees(H) = number of trees in heap H.
• marks(H) = number of marked nodes in heap H.

Then Potential Function of Fibonacci Heaps: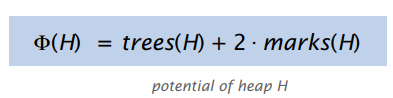
For the figure above,
n = 14, rank = 3, trees(H) = 5, marks(H) = 3
Then, potential of the heap = 5 + 2.3 = 11

Operations

The different operations supported by Fibonacci heap are:

• Find minimum 【O(1)】
• Insertion 【O(1)】
• Union 【O(1)】
• Extract minimum 【O(log N)】
• Decrease key 【O(1)】
• Deletion 【O(log N)】

Find Minimum

Finding minimum is one of the most important operations regarding Fibonacci heaps. A pointer to minimum node of the root list is always kept up to date.

Insertion

Insertion to a Fibonacci heap is similar to the insert operation of a binomial heap. A heap of one element is created and the two heaps are merged with the merge function. The minimum element pointer is updated if necessary. The total number of nodes in the tree increases by one.
To insert a node in a Fibonacci heap H, the following algorithm is followed:

1. Create a new node 'x'.
2. Check whether heap H is empty or not.
3. If H is empty then:
   • Make x as the only node in the root list.
   • Set H(min) pointer to x.
4. Else:
   • Insert x into root list and update H(min).

Example: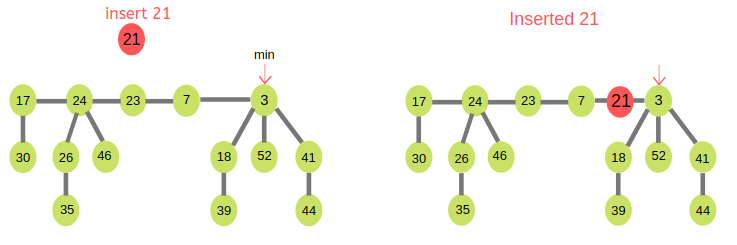

Union

Union concatenates the root lists of two Fibonacci heaps and sets the minimum node to which ever tree’s minimum node is smaller. Union of two Fibonacci heaps Tree1 and Tree2 can be accomplished by following algorithm:

1. Join root lists of Fibonacci heaps Tree1 and Tree2 and make a single Fibonacci heap H.
2. If Tree1(min) < Tree2(min) then:
   • H(min) = Tree1(min).
3. Else:
   • H(min) = Tree2(min).

Example: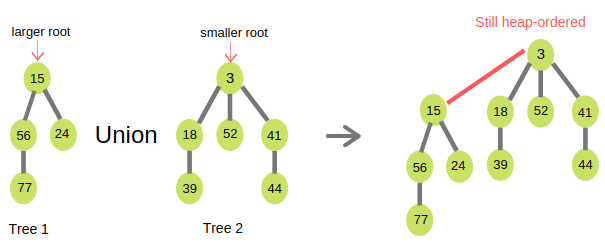

Implementation

//c++ code for creating and 
//inserting a node in Fibonacci heap
#include <iostream> 
#include <algorithm> 
#include <vector> 
using namespace std;
   
struct node
{
   
    node* parent;
    node* child;
    node* left;
    node* right;
    int key;
};
   
//creating a min pointer as NULL
struct node* min = NULL;
   
//for counting the number of nodes in heap
int count = 0;
   
//function to insert a node in the heap
void insert(int val)
{

    struct node* new_node = (struct node*)malloc(sizeof(struct node));
    new_node->parent = NULL;
    new_node->child = NULL;
    new_node->left = new_node;
    new_node->right = new_node;
    new_node->key = val;
       
    if(min != NULL)
    {
        
        (min->left)->right = new_node;
        new_node->right = min;
        new_node->left = min->left;
        min->left = new_node;
        if(new_node->key > min->key){
            min = new_node;
        }
    }
    else
    {
        min = new_node;
    }
    count++;
}
   
// Function to display the heap 
void display(struct node* min) 
{ 
    
    node* ptr = min; 
    if (ptr == NULL)
    {
            
        cout << "The Heap is Empty" << endl; 
    }
    else { 
        cout << "The root nodes of Heap are: " << endl; 
        do { 
        cout << ptr->key; 
        ptr = ptr->right; 
        if (ptr != min) { 
            cout << "-->"; 
                } 
        } while (ptr != min && ptr->right != NULL); 
        cout << endl << "The heap has " << count << " nodes << endl; 
    } 
} 

// Function to find min node in the heap 
void find_min(struct node* min) 
{ 

        cout << "min of heap is: " << min->key << endl; 
} 

Extract Min

It works by first making a root out of each of the minimum node’s children and removing the minimum node from the root list. It then consolidates the root list by linking roots of equal degree until at most one root remains of each degree.
It is one of the most important operations regarding Fibonacci heaps. Much of a Fibonacci heap’s speed advantage comes from the fact that it delays consolidating heaps after operations until extract-min is called. Binomial heaps, on the other hand, consolidate immediately. Consolidation occurs when heap properties are violated, for example, if two heaps have the same order, the heaps must be adjusted to prevent this.
Following algorithm is used for Extract min in a Fibonacci Heap -

1. Delete the min node.
2. Set head to the next min node and add all the tree of the deleted node in root list.
3. Create an array of degree pointers of the size of the deleted node.
4. Set degree pointer to current node.
   Move to the next node.
   • If degrees are different then set degree pointer to next node.
   • If degrees are same then join the Fibonacci trees by union operation.
5. Repeat steps 4 and 5 until the heap is completed.
   

Example: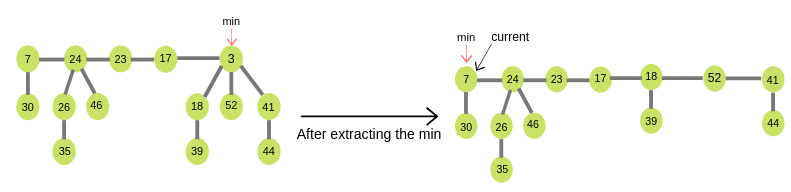

Decrease Key

Decrease key lowers the key of a node. The node is then cut from the tree, joining the root list as its own tree. The parent of the node is then cut if it is marked, this continues for each anscestor until a parent that is not marked is encountered, which is then marked. The pointer to the minimum node is then updated if the node’s new value is less than the current minimum.

Algorithm

1. Decrease the value of the node ‘x’ to the new chosen value.
2. CASE 1 - If min heap order not violated,
   • Update min pointer if necessary.
3. CASE 2 - If min heap order violated and parent of ‘x’ is unmarked,
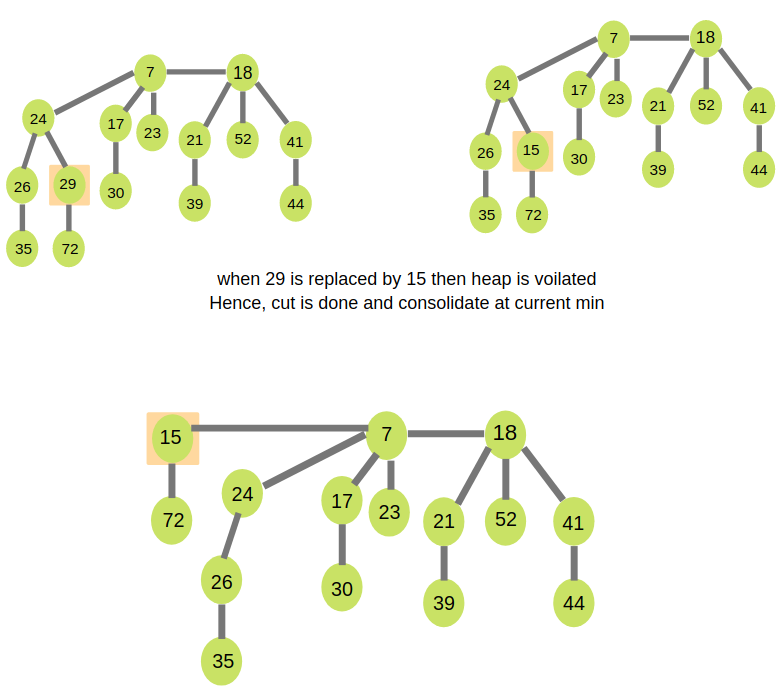
   • Cut off the link between ‘x’ and its parent.
   • Mark the parent of ‘x’.
   • Add tree rooted at ‘x’ to the root list and update min pointer if necessary.
4. CASE 3 - If min heap order is violated and parent of ‘x’ is marked,
   • Cut off the link between ‘x’ and its parent p[x].
   • Add ‘x’ to the root list, updating min pointer if necessary.
   • Cut off link between p[x] and p[p[x]].
   • Add p[x] to the root list, updating min pointer if necessary.
   • If p[p[x]] is unmarked, mark it.
   • Else, cut off p[p[x]] and repeat steps 4.2 to 4.5, taking p[p[x]] as ‘x’.

Example: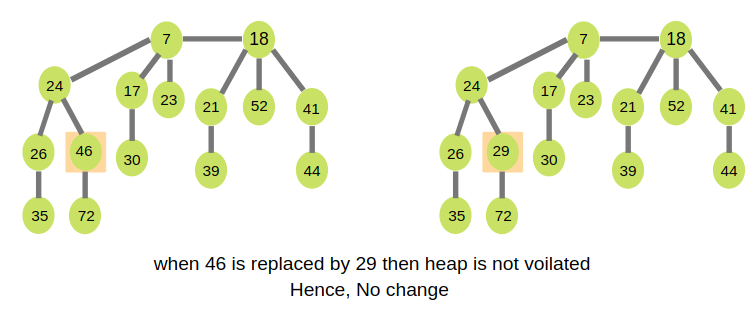

Deletion

Delete is performed by calling decrease key to reduce the node to negative infinity which pulls the node to the top of the tree. Extract minimum is then called on the node to remove it from the heap.

Algorithm

1. Decrease the value of the node to be deleted ‘x’ to minimum by Decrease Key function.
2. By using min heap property, heapify the heap containing ‘x’, bringing ‘x’ to the root list.
3. Apply Extract Min algorithm to the Fibonacci heap.

Implementation

//C++ program to demonstrate Extract min, Deletion() and
//Decrease key() operations in a fibonacci heap
#include <iostream> 
#include <algorithm> 
#include <vector> 
using namespace std;
   //Creating a structure to represent a node in the heap 
    struct node
    { 
        
        node* parent; // Parent pointer 
        node* child; // Child pointer 
        node* left; // Pointer to the node on the left 
        node* right; // Pointer to the node on the right 
        int key; // Value of the node 
        int degree; // Degree of the node 
        char mark; // Black or white mark of the node 
        char c; // Flag for assisting in the Find node function 
    }; 
    
// Creating min pointer as "mini" 
struct node* mini = NULL; 

// Declare an integer for number of nodes in the heap 
int no_of_nodes = 0; 


// Function to insert a node in heap 
void insertion(int val) 
{ 

        struct node* new_node = (struct node*)malloc(sizeof(struct node)); 
        new_node->key = val; 
        new_node->degree = 0; 
        new_node->mark = 'W'; 
        new_node->c = 'N'; 
        new_node->parent = NULL; 
        new_node->child = NULL; 
        new_node->left = new_node; 
        new_node->right = new_node; 
        if (mini != NULL) { 
            (mini->left)->right = new_node; 
            new_node->right = mini; 
            new_node->left = mini->left; 
            mini->left = new_node; 
            if (new_node->key < mini->key) 
                mini = new_node; 
        } 
        else { 
            mini = new_node; 
        } 
        no_of_nodes++; 
} 
    
// Linking the heap nodes in parent child relationship 
void Fibonnaci_link(struct node* ptr2, struct node* ptr1) 
{ 

        (ptr2->left)->right = ptr2->right; 
        (ptr2->right)->left = ptr2->left; 
        if (ptr1->right == ptr1) 
            mini = ptr1; 
        ptr2->left = ptr2; 
        ptr2->right = ptr2; 
        ptr2->parent = ptr1; 
        if (ptr1->child == NULL) 
            ptr1->child = ptr2; 
        ptr2->right = ptr1->child; 
        ptr2->left = (ptr1->child)->left; 
        ((ptr1->child)->left)->right = ptr2; 
        (ptr1->child)->left = ptr2; 
        if (ptr2->key < (ptr1->child)->key) 
            ptr1->child = ptr2; 
        ptr1->degree++; 
}

// Consolidating the heap 
void Consolidate() 
{ 

        int temp1; 
        float temp2 = (log(no_of_nodes)) / (log(2)); 
        int temp3 = temp2; 
        struct node* arr[temp3]; 
        for (int i = 0; i <= temp3; i++) 
            arr[i] = NULL; 
        node* ptr1 = mini; 
        node* ptr2; 
        node* ptr3; 
        node* ptr4 = ptr1; 
        do { 
            ptr4 = ptr4->right; 
            temp1 = ptr1->degree; 
            while (arr[temp1] != NULL) { 
                ptr2 = arr[temp1]; 
                if (ptr1->key > ptr2->key) { 
                    ptr3 = ptr1; 
                    ptr1 = ptr2; 
                    ptr2 = ptr3; 
                } 
                if (ptr2 == mini) 
                    mini = ptr1; 
                Fibonnaci_link(ptr2, ptr1); 
                if (ptr1->right == ptr1) 
                    mini = ptr1; 
                arr[temp1] = NULL; 
                temp1++; 
            } 
            arr[temp1] = ptr1; 
            ptr1 = ptr1->right; 
        } while (ptr1 != mini); 
        mini = NULL; 
        for (int j = 0; j <= temp3; j++) { 
            if (arr[j] != NULL) { 
                arr[j]->left = arr[j]; 
                arr[j]->right = arr[j]; 
                if (mini != NULL) { 
                    (mini->left)->right = arr[j]; 
                    arr[j]->right = mini; 
                    arr[j]->left = mini->left; 
                    mini->left = arr[j]; 
                    if (arr[j]->key < mini->key) 
                        mini = arr[j]; 
                } 
                else { 
                    mini = arr[j]; 
                } 
                if (mini == NULL) 
                    mini = arr[j]; 
                else if (arr[j]->key < mini->key) 
                    mini = arr[j]; 
                } 
           } 
} 

// Function to extract minimum node in the heap 
void Extract_min() 
{ 

        if (mini == NULL) 
            cout << "The heap is empty" << endl; 
        else { 
            node* temp = mini; 
            node* pntr; 
            pntr = temp; 
            node* x = NULL; 
            if (temp->child != NULL) { 
                x = temp->child; 
                do { 
                    pntr = x->right; 
                    (mini->left)->right = x; 
                    x->right = mini; 
                    x->left = mini->left; 
                    mini->left = x; 
                    if (x->key < mini->key) 
                        mini = x; 
                    x->parent = NULL; 
                    x = pntr; 
                } while (pntr != temp->child); 
            } 
            (temp->left)->right = temp->right; 
            (temp->right)->left = temp->left; 
            mini = temp->right; 
            if (temp == temp->right && temp->child == NULL) 
                mini = NULL; 
            else { 
                mini = temp->right; 
                Consolidate(); 
            } 
            no_of_nodes--; 
        } 
} 

// Cutting a node in the heap to be placed in the root         list 
void Cut(struct node* found, struct node* temp) 
{ 

        if (found == found->right) 
            temp->child = NULL; 

        (found->left)->right = found->right; 
        (found->right)->left = found->left; 
        if (found == temp->child) 
            temp->child = found->right; 

        temp->degree = temp->degree - 1; 
        found->right = found; 
        found->left = found; 
        (mini->left)->right = found; 
        found->right = mini; 
        found->left = mini->left; 
        mini->left = found; 
        found->parent = NULL; 
        found->mark = 'B'; 
} 

// Recursive cascade cutting function 
void Cascase_cut(struct node* temp) 
{ 

        node* ptr5 = temp->parent; 
        if (ptr5 != NULL) { 
            if (temp->mark == 'W') { 
                temp->mark = 'B'; 
            } 
            else { 
                Cut(temp, ptr5); 
                Cascase_cut(ptr5); 
            } 
        } 
} 

// Function to decrease the value of a node in the heap 
void Decrease_key(struct node* found, int val) 
{ 

        if (mini == NULL) 
            cout << "The Heap is Empty" << endl; 

        if (found == NULL) 
            cout << "Node not found in the Heap" << endl; 

        found->key = val; 

        struct node* temp = found->parent; 
        if (temp != NULL && found->key < temp->key) { 
            Cut(found, temp); 
            Cascase_cut(temp); 
        } 
        if (found->key < mini->key) 
            mini = found; 
} 

// Function to find the given node 
void Find(struct node* mini, int old_val, int val) 
{ 
	
        struct node* found = NULL; 
        node* temp5 = mini; 
        temp5->c = 'Y'; 
        node* found_ptr = NULL; 
        if (temp5->key == old_val) { 
            found_ptr = temp5; 
            temp5->c = 'N'; 
            found = found_ptr; 
            Decrease_key(found, val); 
        } 
        if (found_ptr == NULL) { 
            if (temp5->child != NULL) 
                Find(temp5->child, old_val, val); 
            if ((temp5->right)->c != 'Y') 
                Find(temp5->right, old_val, val); 
        } 
        temp5->c = 'N'; 
        found = found_ptr; 
} 

// Deleting a node from the heap 
void Deletion(int val) 
{ 

        if (mini == NULL) 
            cout << "The heap is empty" << endl; 
        else { 

            // Decreasing the value of the node to 0 
            Find(mini, val, 0); 

		// Calling Extract_min function to 
		// delete minimum value node, which is 0 
            Extract_min(); 
            cout << "Key Deleted" << endl; 
        } 
} 

// Function to display the heap 
void display() 
{ 

        node* ptr = mini; 
        if (ptr == NULL) 
            cout << "The Heap is Empty" << endl; 

        else { 
            cout << "The root nodes of Heap are: " << endl; 
            do { 
                cout << ptr->key; 
                ptr = ptr->right; 
                if (ptr != mini) { 
                    cout << "-->"; 
                } 
            } while (ptr != mini && ptr->right != NULL); 
            cout << endl << "The heap has " << no_of_nodes << " nodes" << endl << endl; 
        } 
}

Complexity + Comparison

Comparision of time complexities for various operations:

To determine the amortized cost of FIB-HEAP-INSERT, let H be the input Fibonacci heap and H' be the resulting Fibonacci heap. Then, t(H') = t(H) + 1 and m(H') = m(H) and the increase in potential is (t(H) + 1) + 2m(H)) - (t(H) + 2m(H)) = 1.Since the actual cost is O(1), the amortized cost is O(1) + 1 = O(1).

The minimum node of a Fibonacci heap H is given by the pointer H.min, so we can find the minimum node in O(1) actual time. Because the potential of H does not change, the amortized cost of this operation is equal to its O(1) actual cost.