Kosaraju's Algorithm for Strongly Connected Components 【O(V+E)】

Reading time: 30 minutes | Coding time: 15 minutes

Did you know that our Internet is a strongly Connected Graph? and we can test this in linear time. Read on to find more.

The Kosaraju algorithm is a DFS based algorithm used to find Strongly Connected Components(SCC) in a graph. It is based on the idea that if one is able to reach a vertex v starting from vertex u, then one should be able to reach vertex u starting from vertex v and if such is the case, one can say that vertices u and v are strongly connected - they are in a strongly connected sub-graph.

Algorithm

The algorithm consists of three steps:

1. Do a DFS on the original graph: Do a DFS on the original graph, keeping track of the finish times of each node. This can be done using a stack, when a DFS finishes put the source vertex on the stack. This way node with highest finishing time will be on top of the stack.
2. Reverse the original graph: Reverse the graph using an adjaceny list.
3. Do DFS again: Do DFS on the reversed graph, with the source vertex as the vertex on top of the stack. When DFS finishes, all nodes visited will form one Strongly Connected Component. If any more nodes remain unvisited, this means there are more Strongly Connected Component's, so pop vertices from top of the stack until a valid unvisited node is found. This will have the highest finishing time of all currently unvisited nodes. This step is repeated until all nodes are visited.

Pseudocode

stack STACK
void DFS(int source) {
    visited[s]=true
    for all neighbours X of source that are not visited:
        DFS(X)
    STACK.push(source)
}

CLEAR ADJACENCY_LIST
for all edges e:
    first = one end point of e
    second = other end point of e
    ADJACENCY_LIST[second].push(first)
    
while STACK is not empty:
    source = STACK.top()
    STACK.pop()
    if source is visited :
        continue
    else :
        DFS(source)

Implementation

#include <bits/stdc++.h>
#define MAX_N 20001

using namespace std;

int n, m;
struct Node
{
    vector<int> adj;
    vector<int> rev_adj;
};
Node graph[MAX_N];

stack<int> S;
bool visited[MAX_N];

int component[MAX_N];
vector<int> components[MAX_N];
int numComponents;

void DFS1(int x)
{
    visited[x] = true;
    for (int i=0;i<graph[x].adj.size();i++)
    {
        if (!visited[graph[x].adj[i]]) DFS1(graph[x].adj[i]);
    }
    S.push(x);
}

void DFS2(int x)
{
    cout << x << " "; 
    component[x] = numComponents;
    components[numComponents].push_back(x);
    visited[x] = true;
    for (int i=0;i<graph[x].rev_adj.size();i++)
    {
        if (!visited[graph[x].rev_adj[i]]) DFS2(graph[x].rev_adj[i]);
    }
}

void Kosaraju()
{
    for (int i=0;i<n;i++)
    {
        if (!visited[i]) DFS1(i);
    }
    
    for (int i=0;i<n;i++)
    {
        visited[i] = false;
    }
    
    while (!S.empty())
    {
        int v = S.top(); S.pop();
        if (!visited[v])
        {
            printf("Component %d: ", numComponents);
            DFS2(v);
            numComponents++;
            printf("\n");
        }
    }
}

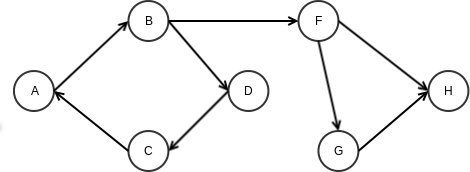
Example

Consider the following graph:



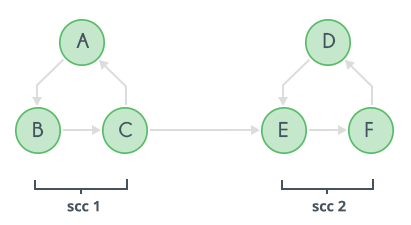
It has two strongly connected components scc1 and scc2.

• Upon performing the first DFS with scc1 as the source, we get the following scenario:

• Upon reversing the graph and performing DFS again with scc2 as the source, we get the following scenario:
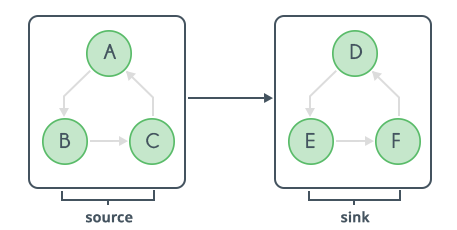
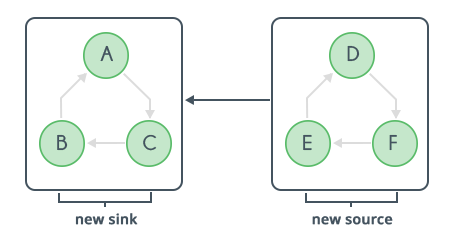We infer that after both the DFS passes, the strongly connected components are clustered together.

Complexity

The time complexity of this algorithm is O(V+E), where V is the number of vertices and E is the number of edges.

Application

• Kosaraju's algorithm is used to find the Strongly Connected Components in a graph in linear time.