Heavy Light Decomposition,a competitive programming algorithm is very useful in solving queries efficiently. We will see its usecase, implementation and finally solve few problems based on it.

Heavy Light Decomposition is an interesting topic and it needs quite a few prequisites which we will be covering through.

Basic Terms:

Segment trees

Segment trees store the sum of elements of an array and are broken down as they move down.
So the array given is of size 5.HereA[x:y] denotes the sum of all elements from A[x] to A[y].The root always stores the total sum.Then we begin by splitting it into left node as A[0:(n-1)/2] and the right node as A[(n-1)/2+1:n-1] as given in the figure.

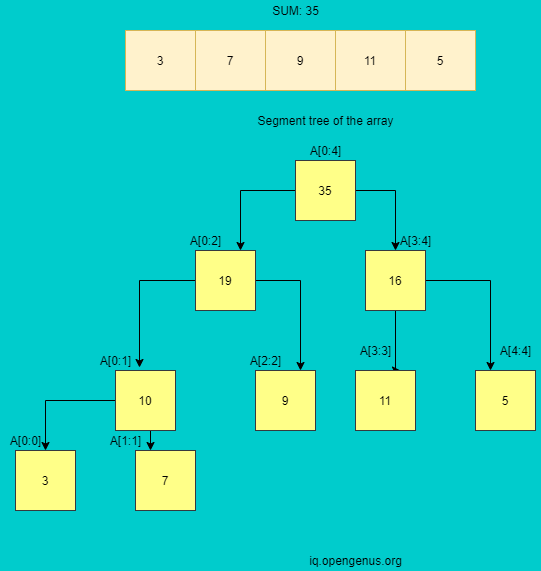
In segment tree, as the node is divided into two halves,its children represent two halves.So the height of the tree is (log2N) .All the leaves are the elements of the array.There are N nodes as leaves.There are N-1 internal nodes.So,total number of nodes:

N-1+N
2N-1

The structure of the segment cannot be changed,but the elements can be updated.We can perform two operations with segment trees:

• Update- to update the element in array A and reflect changes in the segment tree.
• Query-We can return required value like the sum of the path ,maximum or minimum sum and so on .

Segment trees are implemented in the form of arrays.Suppose ith element is parent then their children are 2i ,2i+1.

How to make a segment tree?

//original array and segment tree array.
int orig[N],st[N*6];
//to build the segment tree
void build_seg(int i,int s,int e)
{
//if only node,then its stored in that array.

 if(s==e-1)
   {
    st[i]=orig[e-1];
    return;
   }
   int mid=(s+e)/2;
   
   //for the left part
   
   build_seg(2*i,s,m);
   
   //for the right part
   
   build_seg(2*i+1,m+1,e);
   
   //the node stores the sum of its children
   
   st[i]=st[2*i]+st[2*i+1];
    
}

How to update a value in segment tree?

void update_seg(int v,int l,int r,int pos,int val)
{ //if only one element in st:

    if(l==r)
      {st[v]=val;return;}
      
      int mid=(l+r)/2;
      
     //if the updation is before or at mid index:
     
      if(pos<=mid)
      update_seg(v*2,l,mid,pos,val);
      
     //if its after the mid:
     
      else
      update_seg(2*v+1,mid+1,r,pos,val);
      
      //the node will store the sum of children
      
      st[v]=st[2*v]+st[2*v+1];
}

Depth First Search(DFS)

1. Inorder (left,root,right)
2. Preorder (root,left,right)
3. Postorder(left,right,root)

//let adj[][] be a tree 
void dfs(int cur,int prev,int depths)
{
//store the parent(i.e. prev) of cur node

 parent[0][cur]=prev;
 
 //store the level of the cur node
 depth[cur]=depths;
 //
 subtree_size[cur]=1;
 for(int i:adj[cur].size())
 {
     if(adj[cur][i]!=prev)
       {
          
           dfs(adj[cur][i],cur,depths+1);
           subtree_size[cur]+=subtree_size[adj[cur][i]];
           
       }
 }
}

Lowest Common Ancestor(LCA)

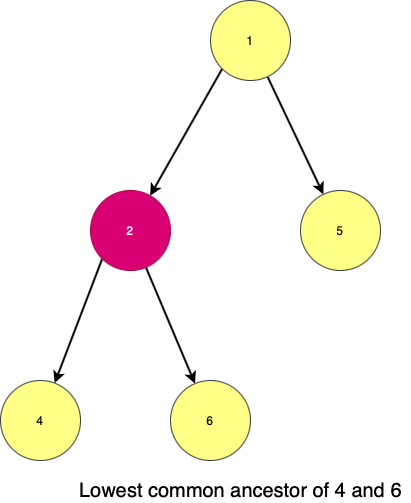
Lowest Common Ancestor : is the node which is at the lowest or the nearest level that is common to both the nodes.
Here in the image,

• 1 is also the common node of 4 and 6 but it is not the nearest node.
• Therefore, 2 being the common node and the nearest to both of them is adjudged as the lowest common ancestor(LCA)
• We will see how we can find ancestors using Recursion,Euler tour and Binary Lifting

Lets find out what is binary lifting before implementing it..

Binary Lifting

Binary Lifting is an efficient method to find the LCA of two nodes in a binary tree.Though we can use recursion and other techniques but this method is good in terms of time complexity.

When you want to find LCA of two nodes,there are two cases:
a. Both of them are at same level.
b. One of them is at lower level.

In case b, we try to make it case a. We bring it to the same level.
And later for both of them alike,we make both the nodes jump together until they reach the LCA.We jump at the rate of 2^k nodes,until we reach the LCA or root reducing complexity to logn time.
We stop both the nodes right at the bottom of the LCA or root.Then we return the LCA .

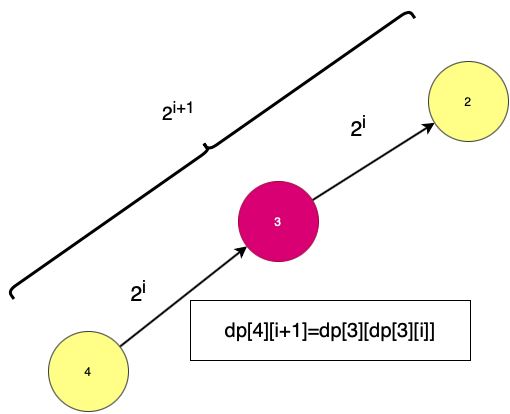
According to the above image,4th node which is 2^(i+1)th distance/level away then the 3rd node is 2^ith distance away.We get the same node when we use both of them.And this way we jump with 2^k jumps.For simplification,we use powers of 2 i.e. k instead of 2^k.

dp[4][i+1]=dp[i][dp[3][i]]
//dp[4][i+1] denotes the 2^(i+1)th ancestor of node 4.

Finding lca

//to store the parent/ancestor of each node
for(int i=1; i<LN; i++)
			for(int j=0; j<n; j++)
				if(parent[i-1][j] != -1)
					parent[i][j] = parent[i-1][parent[i-1][j]];

int lca(int u,int v)
{  
 /*assuming u is at lower level but if actually v is at lower level
 then we swap them*/
 
    if(depth[u]<depth[v]) swap(u,v);
    
    int diff=depth[u]-depth[v];
    
    // we make jumps till the difference is 0
    //a>>b is equivalent to a/2^b
    
    for(int i=0;i<LN;i++)
    if((diff>>i)&1) u=parent[i][u];
    
    //if anyone reaches one another then it is proved that v or 
    //u is the ancestor,so return u.
    
    if(u==v) return u;
    
    //we then make jumps till we reach below lca
    for(int LN-1;i>=0;i--)
    {
        if(parent[i][u]!=parent[i][v])
          u=parent[i][u],v=parent[i][v];
    }
    //we return the ancestor
    return parent[0][u];
    
}

HLD

Introduction

Heavy Light Decomposition is a way through which we can solve or perform queries on trees in a very less amount of time.In heavy light decomposition,as per its name, the tree is cut into many parts-heavy and light.Later on queries can be performed on the tree. For example: Through HLD we can find out the sum in between two edges i and j of the kth ancestor of the element say, p[m]!

• Break the tree into disjoint chains from top to bottom.
• The maximum subtree size's child will be the heavy edge(special child) and the others will be light edge(normal child).
• A new chain starts after every light node.

Properties of a HLD

• Every vertex is part of only one chain.
• Every chain forms a subarray in linearised tree.
• Subtree size reduces by atleast half when traversing the light edge.

To have a special child it should have atleast half of the weight of its parent.So naturally the subtree size reduces by half while going through light edges/normal chilren.

Why do we club all the special children into one chain?
We club all the special children or heavy edges into one chain so as to reduce traversals/jumpings from one segment to other thus decreasing the time complexity.
Nodes of different segment's lca is the root.So to perform any query we just need to keep on moving upwards and perform the required number of operations.

So in query(a,b) , where a and b are part of different segments ,the query can be performed like query(a,LCA) * query(b,LCA) where
(*) is any binary operation like sum for instance.
To find LCA , binary lifting is being used due to its grand jumps to get to the LCA.

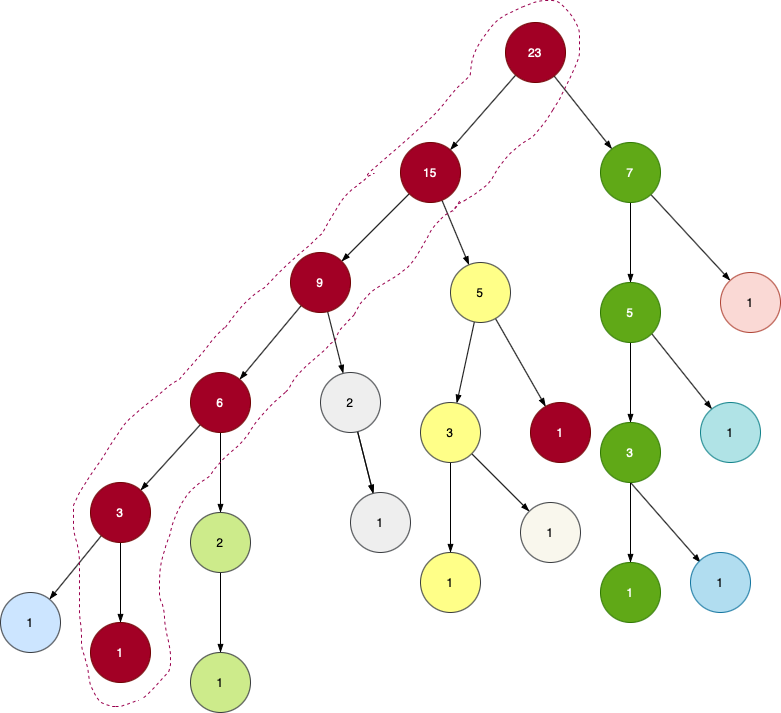
Examine the above tree.We have clubbed all the highest valued nodes in each level into a chain.And then we took the leftover nodes and followed exactly the same procedure.In this manner we are able to break the tree into different and disjoint chains.Each chain's nodes are colored in a specific way.
This tree is looking like a segment tree.So we can definitely use the concept of segment tree to realise HLD.As we see in the figure,that almost all nodes are grouped into chains,this shows that all these chains denote segment trees.

To update any element we need to change in that particular segment tree and simultaneously update the ancestors' values too.

So traversing a segment tree is O(logn) and hence O(logn) time complexity against other methods which have O(n) complexity,which is inefficient in case of long computations.

To perform queries we need to traverse between different chains.We know that since there are atmost logn nodes and traversing each segment trees is O(logn) ,so there can be atmost logn segment trees.

The worst time complexity is O(logn*(total nodes))
(logn*logn)

Implementation

Algorithm

We extend the heavy chain if we find heavy child and form new chains for the normal or light children.When we reach leaf node we stop.

HLD(curNode,curChain):
add current node to current chain
if curNode is a leaf node : return
heavy:=choose child node with max subtree size
Extend the heavy chain: HLD(heavy,curChain)
for every normal or light child:
    if ch not heavy:
         HLD(ch,newChain) // forms different and new normal chains

Pseudocode

//adj[][] is the tree here.

HLD(curNode):
//if the ith chain has no elements then make the curNode as head 

if ith chain is new: chainHead[i]=curNode

//Store the chain number,i.e, of curNode 

chainInd[curNode]=i

//Store the  size of ith chain 

chainPos[curNode]=chainSize[i]

//increment the size of ith chain as a node is added to it
chainSize[i]++

//extend the heavy chain by choosing the heaviest children

for(k:adj[cur].size())
   if(subtree_size[adj[cur][k]]>max_ssize)
     max_ssize=subtree_size[adj[cur][k]],index=k
     
 if(index>=0) HLD(adj[curNode][index])
 
 //for normal children,make a new chain by increasing the chain number i
 
 for(k:adj[curNode].size())
   if(k!=index)
     i++,HLD(adj[curNode][k])

HLD code

//tree 
vector<int> adj[N];

//chain no,size of each chain,the first node of each chain,
//position of each chain,chain index of each node respectively.

int chainNo=0,chainSize[N],chainHead[N],chainPos[N],chainInd[N],subtree_size[N];

void HLD(int currNode)
{
//if the chain has no elements

if(chainHead[chainNo]==-1)
chainHead[chainNo]=currNode;

//store the chain no for the current node

chainInd[currNode]=chainNo;

//store the chain size for the current node

chainPos[currNode]=chainSize[chainNo];

//increment the size of the chain
chainSize[chainNo]++;

//FOR HEAVY NODES

int maxi=-1,index=-1;

for(int i:adj[currNode].size())
{
//find heaviest child ,store the index

if(subtree_size[adj[currNode][i]]>maxi)
maxi=subtree_size[adj[currNode][i]],index=i;
}
//add the node to the heavy chain

if(index>=0) HLD(adj[currNode][index]);

//FOR LIGHT NODES

for(int i:adj[currNode].size())
{
//if the currnode is not a heavy child

if(i!=index)
//form a new chain,run HLD for it.

 chainNo++,HLD(adj[currNode][i]);
 
 }

We will now clearly see the proper application in the problems given below.

Problems

Q.Given a tree with N nodes, and edges numbered 1, 2, 3...N-1.

Perform the following operations:

CHANGE (i,x) : change the cost of the i-th edge to x
or
QUERY (a ,b): ask for the maximum edge cost on the path from node a to node b

(source: SPOJ-Qtree problem)

#include <iostream>
#include <math.h>
#include<vector>
using namespace std;
#define N 10100
#define LN 14

vector <int> adj[N], costs[N], indexx[N];
int chainNo, posInOrig[N],subtree_size[N],otherEnd[N];
int orig[N],st[N*6],depth[N],pa[LN][N],chainInd[N],chainHead[N],qt[N*6];

void build_seg(int i,int s,int e)
{ if(s==e-1)
   {
    st[i]=orig[e-1];
    return;
   }
   int mid=(s+e)/2;
   //for the left part
   build_seg(2*i,s,m);
   //for the right part
   build_seg(2*i+1,m+1,e);
   //the node stores the sum of its children
   st[i]=st[2*i]+st[2*i+1];
    
}
void update_seg(int v,int l,int r,int pos,int val)
{. //if only one element in st:
    if(l==r)
      {st[v]=val;return;}
      
      int mid=(l+r)/2;
     //if the updation is before or at mid index:
      if(pos<=mid)
      update_seg(v*2,l,mid,pos,val);
     //if its after the mid:
      else
      update_seg(2*v+1,mid+1,r,pos,val);
      //the node will store the sum of children
      st[v]=st[2*v]+st[2*v+1];
}
//to find maximum value in between a and b
void query_tree(int cur,int s,int e,int a,int b)
{
//base case
 if(a>=e or s>=b )
 {qt[cur]=-1;return;}
 
 //only one node
 if(s>=a && e<=b)
 {
 qt[cur]=st[cur];
 return;
 }
 //a>>1=> a/2 ;a<<1=>2*a; c|1 => bits(c)+1;
 int c1=cur<<1,c2=c1|1,m=(s+e)>>1;
 
 
  query_tree(c1,s,m,a,b);
  
  query_tree(c2,m,e,a,b);
  
  
  qt[cur]=max(qt[c1],qt[c2]);
  
}
//bring both u and v in same chain;condition: v as ancestor of u
int query_up(int u,int v)
{
    if(u==v) return 0;
    int uc,vc=chainInd[v],res=-1;
    while(true)
    {
    uc=chainInd[u];
    while(true)
    {
    if(u==v) break;
    query_tree(1,0,ptr,posInOrig[v]+1,posInOrig[u]+1);
    if(qt[1]>res) res=qt[1];
    break;
    }
    query_tree(1, 0, ptr, posInOrig[chainHead[uc]], posInOrig[u]+1);
    if(qt[1]>res) res=qt[1];
    u=chainHead[uc];
    u=pa[0][u];
    }
    return res;
}
int lca(int u,int v)
{
    if(depth[u]<depth[v]) swap(u,v);
    int diff=depth[u]-depth[v];
    for(int i=0;i<LN;i++)
    if((diff>>i&1)) u=pa[i][u];
    if(u==v) return u;
    for(int LN-1;i>=0;i--)
    {
        if(pa[i][u]!=pa[i][v])
          u=pa[i][u],v=pa[i][v];
    }
    return pa[0][u];
    
}
void hld(int curNode, int cost, int prev)
{
if(chainHead[chainNo] == -1) {
		chainHead[chainNo] = curNode; // Assign chain head
	}
	chainInd[curNode] = chainNo;
	posInOrig[curNode] = ptr; // Position of this node in baseArray which we will use in Segtree
	orig[ptr++] = cost;

	int sc = -1, ncost;
	// Loop to find special child
	for(int i=0; i<adj[curNode].size(); i++) if(adj[curNode][i] != prev) {
		if(sc == -1 || subsize[sc] < subsize[adj[curNode][i]]) {
			sc = adj[curNode][i];
			ncost = costs[curNode][i];
		}
	}

	if(sc != -1) {
		
		HLD(sc, ncost, curNode);
	}

	for(int i=0; i<adj[curNode].size(); i++) if(adj[curNode][i] != prev) {
		if(sc != adj[curNode][i]) {
			
			chainNo++;
			HLD(adj[curNode][i], costs[curNode][i], curNode);
		}
	}
}
//function to find the max edge
void maxEdge(int u,int v)
{
 int LCA=lca(u,v);
 int chain1=query_up(u,LCA);
 int chain2=query_up(v,LCA);
 if(chain1>chain2) cout<<chain1<<endl;
}
//to change ith element to x
void change(int i,int x)
{
   int k=otherEnd[i];
   update_seg(1,0,ptr,posInOrig[i],x);
}
//let adj[][] be a tree 
void dfs(int cur,int prev,int depths)
{
//store the parent(i.e. prev) of cur node

 parent[0][cur]=prev;
 
 //store the level of the cur node
 depth[cur]=depths;
 //
 subtree_size[cur]=1;
 for(int i:adj[cur].size())
 {
     if(adj[cur][i]!=prev)
       {
          otherEnd[indexx[cur][i]] = adj[cur][i];
           dfs(adj[cur][i],cur,depths+1);
           subtree_size[cur]+=subtree_size[adj[cur][i]];
           
       }
 }
}
int main()
{
//take all the inputs
chainNo=0;
// set all nodes of pa[i][j]=-1,chainHead[i]=-1,ptr=0,root=-1;
dfs(root,-1);
hld(root,-1,-1);
build_seg(1,0,ptr);
//enter values of a,b within range of the orig array.
maxEdge(a-1,b-1);
change(a-1,b);


}

You can practice more problems on HLD here:

HLD problems

Applications

There are many applications.Here are some real life problems for which HLD is being used:

• Used in fault diagnosis of fiber-optic networks.
• In decoding grammar-based codes
• Graph drawing and greedy embedding.

Now you know what is HLD and how it is used to fastly solve various range query and update problems.We have also seen how HLD can be used to solve real life problems too.HLD is one of the most important competitive coding algorithm and a fun learn too!
Thankyou!