
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes | Coding time: 20 minutes
K Dimensional tree (or k-d tree) is a tree data structure that is used to represent points in a k-dimensional space. It is used for various applications like nearest point (in k-dimensional space), efficient storage of spatial data, range search etc.
Although it might look like a quadtree and octree's generalized version, its implementation quite different. Any internal node in this structure divides the space into 2 halfs. The left child of the node represents the left half while right child represents right half. The space is divided into 2 halves irrespective of the number of dimensions. To be more accurate, every internal node represents a hyperplane that cuts the space in 2 parts. For 2-dimensional space, that is a line and for 3 dimensional space, that is a plane.
Every node in the tree represents a point in the space. General procedure to construct a k-d tree is to recursively divide the space in 2 parts along the axis that has widest spread. Every node in the tree indicates along which dimension the space was divided by the node.
Algorithm
The algorithms below consider the space to be 2 dimensional but can be applied to any space.
-
Search(x, y): This function checks if the point exists in space. Start with root node as current node.
- If the current node represents the point (x, y), return true.
- If current node is not a leaf node, goto step 3, otherwise return false.
- Let current node be the point (X, Y). If the node divides space along x-axis, compare x with X. If x < X, set current node as left child, otherwise set current node as right child. If the node divided the space along y-axis, compare y and Y.
Goto step 1.
-
Insert(x, y): Every insert operation divides the space. The algorithm here considers space to be 2-dimensional but is applicable in all dimensions:
- Search the tree for (x, y) until a leaf node is reached.
- If the tree is empty, add a new node as root representing the point (x, y). Here, the space can be divided along any axis. Indicate the axis along which the space is divided and end insertion.
- Insert a new node where the point (x, y) should have existed and have it store (x, y). If the parent divided the space along x-axis, have the point divide the space along y-axis, otherwise have it divide space along x-axis.
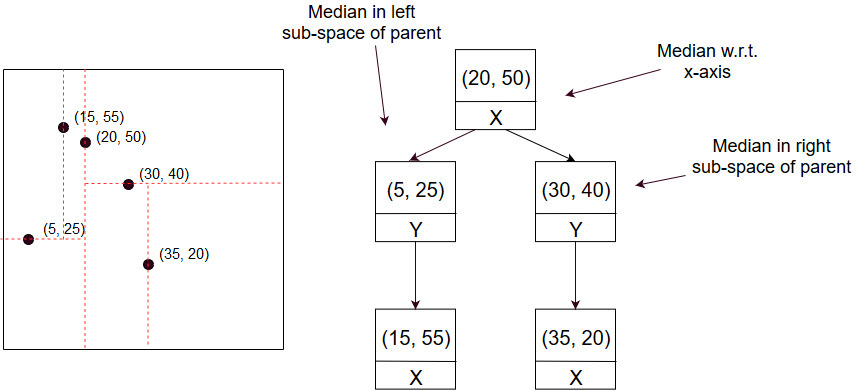
In case the tree is to be built from a given set of points, the strategy to follow is to find the median point with respect to space to be divided. Insert that point using above method and repeat to find children nodes.
Consider the insertion of points: (5, 25), (15, 55), (30, 40), (35, 20), (50, 50) in order. It can be illustrated as:
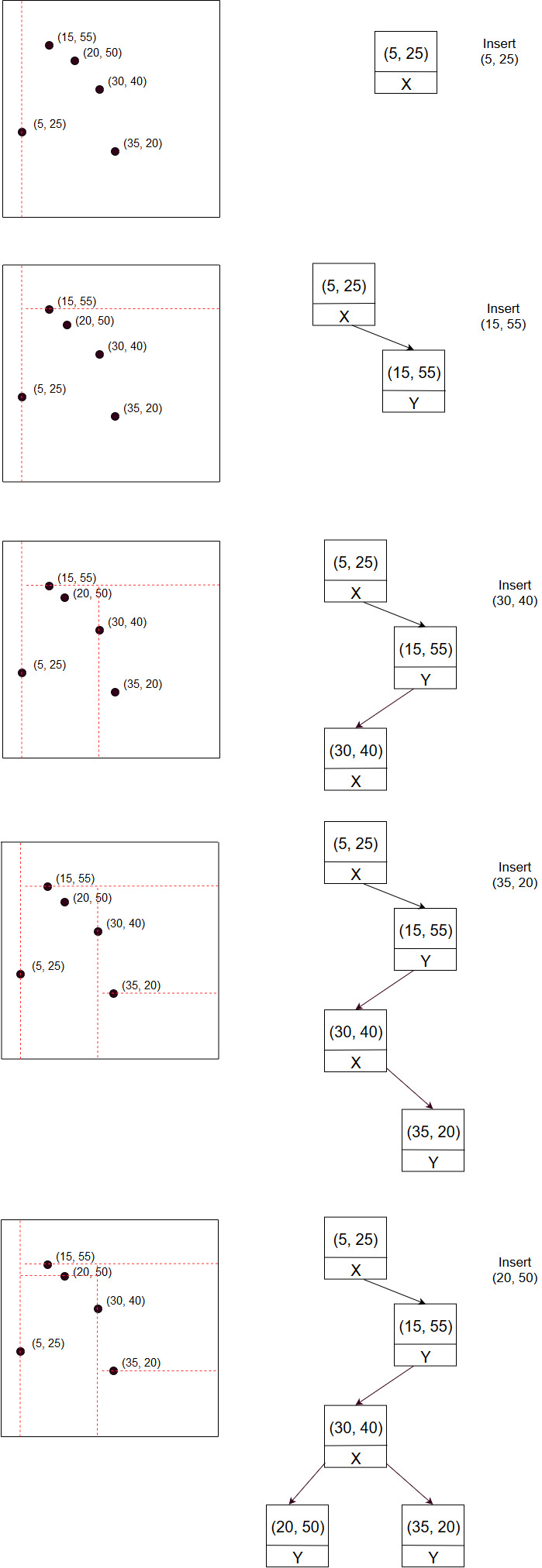
It is important to note that building the tree from a given set of points gives a balanced tree while there is no such gurantee on consecutive inserions. Using median stratergy, the tree would look like:
Complexity
- Time complexity:
- Find: θ(log2N), O(N)
- Insert: θ(log2N), O(N)
- Search: θ(log2N), O(N)
- Space complexity: O(N)
Where N is the count of points.
Implementations
C++ 11
/*
* Code for a k-d tree implementaion for a 2-dimensional space.
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <functional>
#include <utility>
struct point{
int x, y;
};
struct Node{
point *p;
Node *left;
Node *right;
Node(point &p_){
p = new point({p_.x, p_.y});
left == nullptr;
right == nullptr;
}
};
class KDTree{
private:
Node *root;
Node * insert(point &p, Node *node){
if(node == nullptr){
node = new Node(p);
return node;
}
if(node->p->x > p.x){
node->left = insert(p, node->left);
}
else{
node->right = insert(p, node->right);
}
return node;
}
void traverse(Node *node){
if (node == nullptr)
return;
std::cout << node->p->x << ' ' << node->p->y << '\n';
traverse(node->left);
traverse(node->right);
}
int getMedian(std::vector<point> &points, int l, int r, bool x){
if(l == r){
return l;
}
if(x){
return (l + r) >> 1;
}
std::priority_queue<std::pair<int, int>> p1;
std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>,
std::greater<std::pair<int, int>>> p2;
int mid = points[l].y;
p1.push(std::make_pair(mid, l));
for(int i = l + 1; i <= r; ++i){
int temp = points[i].y;
if(p1.size() > p2.size()){
if(temp < mid){
p2.push(p1.top());
p1.pop();
p1.push(std::make_pair(temp, i));
}
else{
p2.push(std::make_pair(temp, i));
}
mid = p1.top().first;
}
else if(p1.size() == p2.size()){
if(temp < mid){
p1.push(std::make_pair(temp, i));
mid = p1.top().first;
}
else{
p2.push(std::make_pair(temp, i));
mid = p2.top().first;
}
}
else{
if(temp < mid){
p1.push(std::make_pair(temp, i));
}
else{
p1.push(p2.top());
p2.pop();
p2.push(std::make_pair(temp, i));
}
mid = p2.top().first;
}
}
if(p2.size() > p1.size()){
return p2.top().second;
}
else{
return p1.top().second;
}
}
void insert(std::vector<point> &points, int l, int r, bool x){
// std::cout << l << ' ' << r << '\n';
if(l > r)
return;
int median = getMedian(points, l, r, x);
insert(points[median]);
insert(points, l, median - 1, x ^ 1);
insert(points, median + 1, r, x ^ 1);
}
public:
KDTree(){
root = nullptr;
}
void insert(point p){
if(root == nullptr){
root = new Node(p);
return;
}
insert(p, root);
}
void insert(std::vector<point> &points){
// function to insert medians.
// proper implementation would require use of a data
// structure like segment tree
// sort the points with respect to x
std::sort(points.begin(), points.end(),
[](const point &l, const point &r) -> bool {
if (l.x == r.x)
return l.y < r.y;
else
return l.x < r.x;
});
insert(points, 0, points.size() - 1, true);
}
void traverse(){
// preorder traversal
traverse(root);
}
};
int main(){
std::vector<point> points = {{20, 50},
{5, 25},
{15, 55},
{30, 40},
{35, 20}};
KDTree tree;
tree.insert(points);
// tree.insert(point({1, 2}));
// tree.insert(point({-1, 2}));
// tree.insert(point({3, 2}));
// tree.insert(point({2, 2}));
tree.traverse();
return 0;
}Applications
- Used extensively in 3D computer graphics, especially game design.
- Used for nearest neighbour search
- Used in spatial database engines.
References/ Further reading
- Rosetta code.
- Wikipedia article on K-Dimensional tree.
