
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
Quadtree is a tree data structure which is used to represent 2-dimensional space. It finds major applications in computer graphics where it is used to represent relations between objects in a 2D space. Quadtrees can also used for image compression, where each internal node has 4 children and stores the average of its children.
Like a binary tree divides a 1-dimensional space into two segments, a quadtree subdivides the space into four quadrants with each quadrant represented by a node.
A point-region quadtree, i.e. PR Quadtree is discussed here. This is used to store to store points in a 2D space such that each leaf represents only one point or no point at all. The internal nodes represents rectangular regions in 2D space. A PR quadtree is used to answer search queries in logarithmic time.
The image below shows how a quadtree changes with insertion:
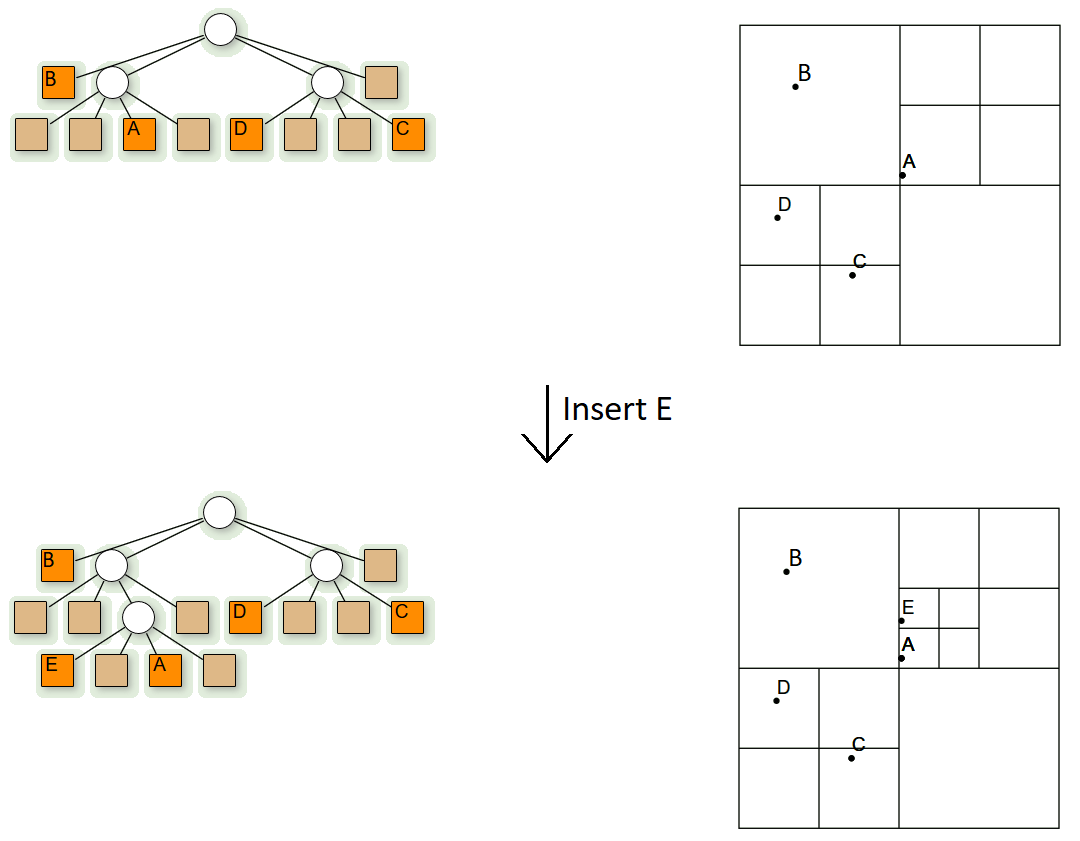
Algorithm
- Three types of nodes are used in quadtree:
- Point node: Used to represent of a point. Is always a leaf node.
- Empty node: Used as a leaf node to represent that no point exists in the region it represent.
- Region node: This is always an internal node. It is used to represent a region.
A region node always have 4 children nodes that can either be a point node or empty node.
Insertion in QuadTree
- Insertion: This is a recursive function used to store a point in the quadtree.
1. Start with root node as current node.
2. If the given point is not in boundary represented by current node, stop insertion
with error.
3. Determine the appropriate child node to store the point.
4. If the child node is empty node, replace it with a point node representing the
point. Stop insertion.
5. If the child node is a point node, replace it with a region node. Call insert for
the point that just got replaced. Set current node as the newly formed region
node.
6. If selected child node is a region node, set the child node as current node.
Goto step 2.Search in QuadTree
- Search: This is a boolean function used to determine weather a point exists in 2D space or not.
1. Start with root node as current node.
2. If the given point is not in boundary represented by current node, stop search
with error.
3. Determine the appropriate child node to store the point.
4. If the child node is empty node, return FALSE.
5. If the child node is a point node and it matches the given point return
TRUE, otherwise return FALSE.
6. If the child node is a region node, set current node as the child region node.
Goto step 2.Complexity
- Time complexity:
- Find: O(log2N)
- Insert: O(log2N)
- Search: O(log2N)
- Space complexity: O(k log2N)
Where k is count of points in the space and space is of dimension N x M, N >= M.
Implementations
C++ 11
/*
* PR Quad tree. Macros are used to easily access children nodes.
*/
#include <iostream>
#include <vector>
#define TL 0 // top left
#define TR 1 // top right
#define BR 2 // bottom right
#define BL 3 // bottom left
struct Point{
int x;
int y;
Point() : x(-1), y(-1) {}
Point(int a, int b) : x(a), y(b) {}
};
class QuadTree{
// if point == NULL, node is regional.
// if point == (-1, -1), node is empty.
Point *point;
Point *top_left, *bottom_right; // represents the space.
std::vector<QuadTree *> children;
public:
QuadTree(){
// to declare empty node
point = new Point();
}
QuadTree(int x, int y){
// to declare point node
point = new Point(x, y);
}
QuadTree(int x1, int y1, int x2, int y2){
if(x2 < x1 || y2 < y1)
return;
point = nullptr;
top_left = new Point(x1, y1);
bottom_right = new Point(x2, y2);
children.assign(4, nullptr);
for(int i = TL; i <= BL; ++i)
children[i] = new QuadTree();
}
void insert(int x, int y){
if(x < top_left->x || x > bottom_right->x
|| y < top_left->y || y > bottom_right->y)
return;
int midx = (top_left->x + bottom_right->x) >> 1,
midy = (top_left->y + bottom_right->y) >> 1;
int pos = -1;
if(x <= midx){
if(y <= midy)
pos = TL;
else
pos = BL;
}
else{
if(y <= midy)
pos = TR;
else
pos = BR;
}
if(children[pos]->point == nullptr){
// if region node
children[pos]->insert(x, y);
return;
}
else if(children[pos]->point->x == -1){
// if empty node
delete children[pos];
children[pos] = new QuadTree(x, y);
return;
}
else{
int x_ = children[pos]->point->x,
y_ = children[pos]->point->y;
delete children[pos];
children[pos] = nullptr;
if(pos == TL){
children[pos] = new QuadTree(top_left->x, top_left->y,
midx, midy);
}
else if(pos == TR){
children[pos] = new QuadTree(midx + 1, top_left->y,
bottom_right->x, midy);
}
else if(pos == BR){
children[pos] = new QuadTree(midx + 1, midy + 1,
bottom_right->x, bottom_right->y);
}
else{
children[pos] = new QuadTree(top_left->x, midy + 1,
midx, bottom_right->y);
}
children[pos]->insert(x_, y_);
children[pos]->insert(x, y);
}
}
bool find(int x, int y){
if(x < top_left->x || x > bottom_right->x
|| y < top_left->y || y > bottom_right->y)
return 0;
int midx = (top_left->x + bottom_right->x) >> 1,
midy = (top_left->y + bottom_right->y) >> 1;
int pos = -1;
if(x <= midx){
if(y <= midy)
pos = TL;
else
pos = BL;
}
else{
if(y <= midy)
pos = TR;
else
pos = BR;
}
if(children[pos]->point == nullptr){
// if region node
return children[pos]->find(x, y);
}
else if(children[pos]->point->x == -1){
// if empty node
return 0;
}
else{
if(x == children[pos]->point->x && y == children[pos]->point->y)
return 1;
}
return 0;
}
};
int main() {
QuadTree tree(1, 1, 4, 4);
std::cout << "Insert (3, 3)\n";
tree.insert(3, 3);
std::cout << "Insert (4, 4)\n";
tree.insert(4, 4);
std::cout << "Insert (1, 4)\n";
tree.insert(1, 4);
std::cout << "Find (3, 3):\n";
std::cout << (tree.find(3, 3) ? "True\n" : "False\n");
std::cout << "Find (3, 4):\n";
std::cout << (tree.find(3, 4) ? "True\n" : "False\n");
return 0;
}Applications
- Used extensively in computer graphics.
- Used for image compression.
- Used to represent spatial relations.
