Fibonacci Search

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 20 minutes | Coding time: 10 minutes

Fibonacci search is an efficient search algorithm based on divide and conquer principle that can find an element in the given sorted array with the help of Fibonacci series in O(log N) time complexity. This is based on Fibonacci series which is an infinite sequence of numbers denoting a pattern which is captured by the following equation:

F(n+1)=F(n)+F(n-1)

where F(i) is the ith number of the Fibonacci series where F(0) and F(1) are defined as 0 and 1 respectively.

The first few Fibonacci numbers are:

0,1,1,2,3,5,8,13....

F(0) = 0
F(1) = 1
F(2) = F(1) + F(0) = 1 + 0 = 1
F(3) = F(2) + F(1) = 1 + 1 = 2
F(4) = F(3) + F(2) = 1 + 2 = 3 and so continues the series

Other searches like binary search also work for the similar principle on splitting the search space to a smaller space but what makes Fibonacci search different is that it divides the array in unequal parts and operations involved in this search are addition and subtraction only which means light arithmetic operations takes place and hence reducing the work load of the computing machine.

Algorithm

Let the length of given array be n [0...n-1] and the element to be searched be x.

Then we use the following steps to find the element with minimum steps:

Find the smallest Fibonacci number greater than or equal to n. Let this number be fb(M) [m’th Fibonacci number]. Let the two Fibonacci numbers preceding it be fb(M-1) [(m-1)’th Fibonacci number] and fb(M-2) [(m-2)’th Fibonacci number].
While the array has elements to be checked:
-> Compare x with the last element of the range covered by fb(M-2)
-> If x matches, return index value
-> Else if x is less than the element, move the third Fibonacci variable two Fibonacci down, indicating removal of approximately two-third of the unsearched array.

-> Else x is greater than the element, move the third Fibonacci variable one Fibonacci down. Reset offset to index. Together this results into removal of approximately front one-third of the unsearched array.

Since there might be a single element remaining for comparison, check if fbMm1 is '1'. If Yes, compare x with that remaining element. If match, return index value.

From the above algorithm it is clear if we have to search the larger section of the array then the time taken will be more and will result into worst case and it's complexity wil be O(log n). If on the very first search, we get our element then it will be considered as the best case and complexcity will be O(1). When we consider the average case then case left and lies between the best and worst i when we have to search the element on the smaller section of the array and hence we get our average case complexity as O(log n).

Example

Let the given array be :

The element do be found be 100

According to the algorithm we will first sort the array.

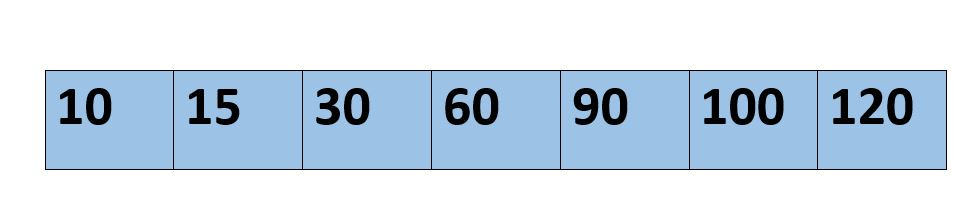
Then check the value in Fibonacci series which is greater or equal to value of n=7

7 <=8
fbM=8 fbM1=5 fbM2=3 offset=-1
i=2 //-1+3 < 7 min((offset+fBM2),n-1)

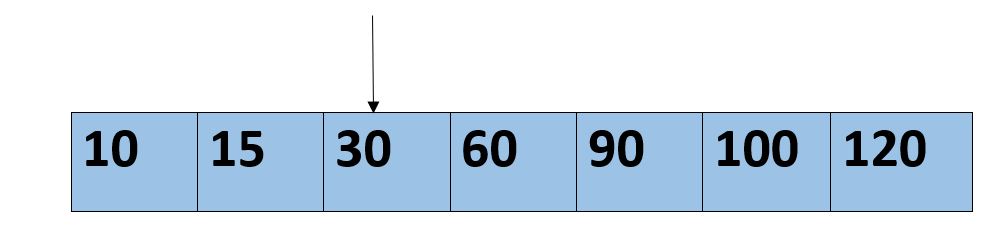
A[2]=30 < 100
fbM=5 fbM1=3 fbM2=2 offset=2
i=5//2+3<7 min((offset+fBM2),n-1)

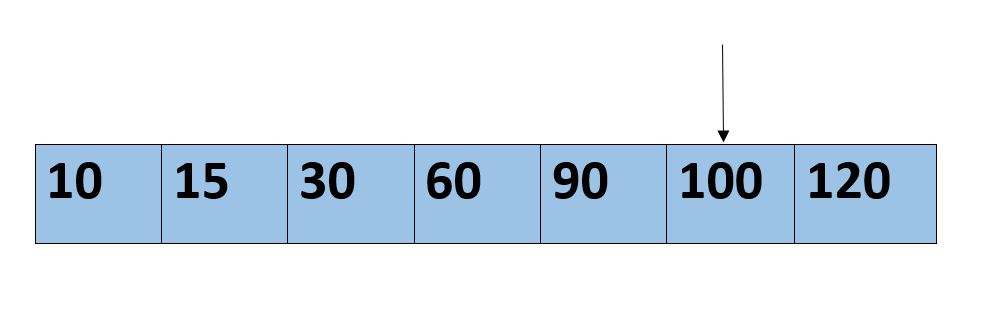
A[5]=100 = 100
Hence number found in 5th position

Pseudocode

The pseudocode of the Fibonacci search algorithm is:


/* Returns index of x if present,  else returns -1 */
int fibonaccianSearch(int arr[], int x, int n)
{
    /* Initialize fibonacci numbers */
    int fbM2 = 0;   // (m-2)'th Fibonacci number
    int fbM1 = 1;   // (m-1)'th Fibonacci number
    int fbM = fbM2 + fbM1;  // m'th Fibonacci
    // Marks the eliminated range from front
    int offset = -1;
    /* fbM is going to store the smallest Fibonacci
       number greater than or equal to n */
    while (fbM < n)
    {
	fbM2 = fbM1;
	fbM1 = fbM;
	fbM  = fbM2 + fbM1;
    }
    /* while there are elements to be inspected. Note that
       we compare arr[fbM2] with x. When fbM becomes 1,
       fbMm2 becomes 0 */
    while (fbM > 1)
    {
	// Check if fbMm2 is a valid location
	int i = min(offset+fbM2, n-1);

	/* If x is greater than the value at index fbMm2,
	   cut the subarray array from offset to i */
	if (arr[i] < x)
	{
	    fbM  = fbM1;
	    fbM1 = fbM2;
	    fbM2 = fbM - fbM1;
	    offset = i;
	}

	/* If x is greater than the value at index fbMm2,
	   cut the subarray after i+1  */
	else if (arr[i] > x)
	{
	    fbM  = fbM2;
	    fbM1 = fbM1 - fbM2;
	    fbM2 = fbM - fbM1;
	}

	/* element found. return index */
	else return i;
    }

    /* comparing the last element with x */
    if(fbM1 && arr[offset+1]==x)
	return offset+1;

    /*element not found. return -1 */
    return -1;

Implementations

C++


#include<iostream.h>
#include<conio.h>
/* Find min of given number */
int min(int x, int y)
{
    return (x<=y)? x : y;
}
/* Returns index of x if present,  else returns -1 */
int fibonaccianSearch(int arr[], int x, int n)
{
    /* Initialize fibonacci numbers */
    int fbM2 = 0;   // (m-2)'th Fibonacci number
    int fbM1 = 1;   // (m-1)'th Fibonacci number
    int fbM = fbM2 + fbM1;  // m'th Fibonacci
    // Marks the eliminated range from front
    int offset = -1;
    /* fbM is going to store the smallest Fibonacci
       number greater than or equal to n */
    while (fbM < n)
    {
        fbM2 = fbM1;
        fbM1 = fbM;
        fbM  = fbM2 + fbM1;
    }
    /* while there are elements to be inspected. Note that
       we compare arr[fibM2] with x. When fbM becomes 1,
       fbM2 becomes 0 */
    while (fbM > 1)
    {
    // Check if fbM2 is a valid location
    int i = min(offset+fbM2, n-1);
    /* If x is greater than the value at index fbM2,
       cut the subarray array from offset to i */
    if (arr[i] < x)
    {
        fbM  = fbM1;
        fbM1 = fbM2;
        fbM2 = fbM - fbM1;
        offset = i;
    }
    /* If x is greater than the value at index fbMm2,
       cut the subarray after i+1  */
    else if (arr[i] > x)
    {
        fbM  = fbM2;
        fbM1 = fbM1 - fbM2;
        fbM2 = fbM - fbM1;
    }
    /* element found. return index */
    else return i;
    }
    /* comparing the last element with x */
    if(fbM1 && arr[offset+1]==x)
    return offset+1;
    /*element not found. return -1 */
    return -1;
}
/* main function */
int main(void)
{
    clrscr();
    int l;
    cout<<"\nEnter the number of elements in array which should be less than 10";
    cin>>l;
    int arr[10];
    cout<<"Enter elements in array";
    for(int i=0;i<l;i++)
    {
    cin>>arr[i];
    }
    int n = sizeof(arr)/sizeof(arr[0]);
    int x;
    cout<<"\nEnter element to be searched :" ;
    cin>>x;
    cout<<"Found at index:"<<fib1onaccianSearch(arr, x, n);
    getch();
    return 0;
}

Complexity

Worst case time complexity: Θ(logn)
Average case time complexity: Θ(log n)
Best case time complexity: Θ(1)
Space complexity: Θ(1)

With each step, the search space is reduced by 1/3 on average, hence, the time complexity is O(log N) where the base of the logarithm is 3.

Applications

Key points about Fibonacci search are:

Fibonacci Search examines closer elements in few steps. So when input array is big that cannot fit in CPU cache or in RAM, it is useful.
On average, fibonacci search requires 4% more comparisons than binary search
Fibonacci search requires only addition and subtraction whereas binary search requires bit-shift, division or multiplication operations.
Fibonacci search can reduce the time needed to access an element in a random access memory.
On magnetic tape where seek time depends on the current head position, there are two considerations: longer seek time and more comparisons that leads to prefer Fibonacci search

According to you which search is better binary or fibonacci?

Fibonacci

Binary

Depends on the requirement

Both

As mentioned above Fibonacci search is an algorithm which uses addition and subtraction and not division or multiplication for searching the element hence the work on hardware is reduced that is calculations done are faster. It would be said that understanding Binary search is easy but for the computer implementation of Fibonacci search is much easier.