Cycle Sort

Reading time: 20 minutes | Coding time: 10 minutes

Algorithm

Consider an array of n distinct elements.

An element a is given, index of a can be calculated by counting the number of elements that are smaller than a.

1. If the element is found to be at its correct position, simply leave it as it is.
2. Otherwise, find the correct position of a by counting the total number of elements that are less than a. where it must be present in the sorted array. The other element b which is replaced is to be moved to its correct position. This process continues until we got an element at the original position of a.

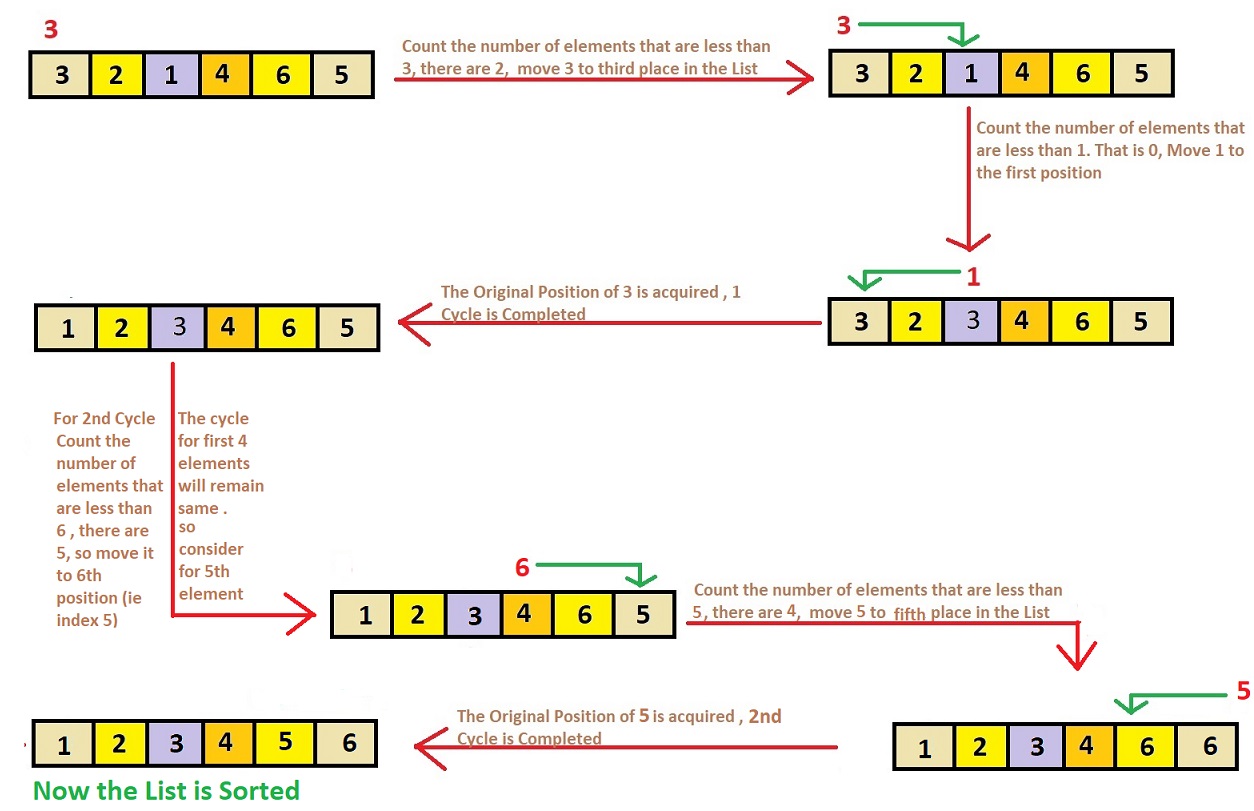
Example

Example 1: Assume the Unsorted input array is: [3, 2, 1, 4, 6, 5].

Based on above algorithm we will illustrate the process which constitutes a cycle. We one by one consider all cycles. We first consider the cycle that includes first element. We find correct position of first element, place it at its correct position, say j. We consider old value of arr[j] and find its correct position, we keep doing this till all elements of current cycle are placed at correct position, i.e., we do not come back to cycle starting point.

Pseudocode

Begin

 for start := 0 to n – 2 do
    key := array[start]
    location := start
    for i := start + 1 to n-1 do
      if array[i] < key then
         location:=location +1
    done

    if location = start then
        ignore lower part, go for next iteration
    while key = array[location] do
        location := location +1
    done

    if location ≠ start then
        swap array[location] with key
    while location ≠ start do
        location := start
        for i := start + 1 to n-1 do
               if array[i] < key then
                    location:=location +1
        done

        while key = array[location]
               location := location +1
        if key ≠ array[location]
               swap array[location] and key
  done
 done
End

Complexity Analysis

Best case time complexity:O(n^2)

Average case time complexity:O(n^2)

Worst case time complexity:O(n^2)

Space complexity:O(1)

This sorting algorithm is best suited for situations where memory write or swap operations are costly.

Here, in this comparison based sorting algorithm the time complexity will remain same for all case (i.e. Best, Average & worst cases) that is O(n^2) as in each iteration, we have to traverse the entire subarray, starting from current position, to count the no. of all the elements that are less than the current element. So, whether or not the array is already sorted or not has no consequence on the running time, nor does it provide an opportunity for optimization and the algorithm must run in quadratic time.

Also, This sorting algorithm is inplace so it does not use any extra memory to sort the array and so that's why it's Space Complexity is constant

Implementation

• C
• Java

#include<stdio.h>
void sort(int a[], int n)  
{  
    int writes = 0,start,element,pos,temp,i;
    for (start = 0; start <= n - 2; start++) {  
        element = a[start];  
        pos = start;  
        for (i = start + 1; i < n; i++)  
            if (a[i] < element)  
                pos++;  
        if (pos == start)  
            continue;  
        while (element == a[pos])  
            pos += 1;  
        if (pos != start) {    
        temp = element;  
        element = a[pos];  
            a[pos] = temp;    
            writes++;  
        }  
        while (pos != start) {  
            pos = start;  
            for (i = start + 1; i < n; i++)  
                if (a[i] < element)  
                    pos += 1;  
            while (element == a[pos])  
                pos += 1;  
            if (element != a[pos]) {  
              temp = element;  
          element = a[pos];  
              a[pos] = temp;    
                writes++;  
            }  
        }  
    }
}
int main()  
{  
    int a[] = {1, 9, 2, 4, 2, 10, 45, 3, 2};  
    int n = sizeof(a) / sizeof(a[0]),i;  
    sort(a, n);  
    printf("After sort, array : ");  
    for (i = 0; i < n; i++)  
        printf("%d  ",a[i]);  
    return 0;  
}  

import java.io.*; 
import java.util.*; 
public class CycleSort   
{  
static void sort(int a[], int n)  
{  
    int writes = 0,start,element,pos,temp,i;  
for (start = 0; start <= n - 2; start++) {  
    element = a[start];  
    pos = start;  
    for (i = start + 1; i < n; i++)  
        if (a[i] < element)  
            pos++;  
    if (pos == start)  
        continue;  
    while (element == a[pos])  
        pos += 1;  
    if (pos != start) {  
    temp = element;  
    element = a[pos];  
        a[pos] = temp;    
        writes++;  
    }  
    while (pos != start) {  
        pos = start;  
        for (i = start + 1; i < n; i++)  
            if (a[i] < element)  
                pos += 1;  
        while (element == a[pos])  
            pos += 1;  
        if (element != a[pos]) {  
          temp = element;  
      element = a[pos];  
          a[pos] = temp;    
            writes++;  
        }  
    }  
}  

}

public static void main(String[] args)

{

int a[] = { 1, 9, 2, 4, 2, 10, 45, 3, 2 };

int n = a.length,i;

sort(a, n);

System.out.println("After sort, array : ");

for (i = 0; i < n; i++)

System.out.println(a[i]);

}

}

Advantages

• Cycle Sort offers the advantage of little or no additional storage.
• It is an in-place sorting Algorithm .
• It is optimal in terms of number of memory writes. It makes minimum number of writes to the memory and hence efficient when array is stored in EEPROM or Flash. Unlike nearly every other sort (Quick , insertion , merge sort), items are never written elsewhere in the array simply to push them out of the way of the action. Each value is either written zero times, if it's already in its correct position, or written one time to its correct position.This matches the minimal number of overwrites required for a completed in-place sort.

Disadvantages

• It is not mostly used because it has more time complexity (i.e O(n^2)) than any other comparison sorting algorithm.

Application

• This sorting algorithm is best suited for situations where memory write or swap operations are costly.