
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 12 minutes
Tarjan's Algorithm is an efficient graph algorithm to find the strongly connected components in a directed graph in linear time by utilizing Depth First Search traversal of a graph. The key idea used is that nodes of strongly connected component form a subtree in the DFS spanning tree of the graph.
The task of partitioning a directed graph into its Strongly Connected Components is of high importance and is used extensively in various problems. Two algorithms used for this purpose are:
- Tarjan's algorithms
- Kosaraju's algorithm
We will explore Tarjan's algorithm in this article.
Before proceeding further, we will revisit the two basic concepts/ terminologies in graph:
- strongly connected graph
- strongly connected component
A directed graph is called strongly connected if each vertex of the graph is reachable from every other vertex in the graph. This means that a path would exist between each pair of nodes.
For a directed graph, a strongly connected component is a parition or a subgraph, which is not a subgraph of another strongly connected component. This means that a strongly connected component has to be the maximal subgraph satisfying the condition. Henceforth, we will refer to strongly connected components using the abbreviated term SCC.
Algorithm
It utilizes the property that nodes of strongly connected component form a subtree in the DFS spanning tree of the graph.
The steps involved are:
- A dfs is run over the nodes and the subtrees of SCCs are removed and recorded as they are encounered.
- Two values dfs_num(u) and dfs_low(u) are maintained for each of the users. dfs_num(u) is the value of the counter when the node u is explored for the first time. dfs_low(u) stores the lowest dfs_num reachable from u which is not the part of another SCC.
- As the nodes are explored, they are pushed onto a stack.
- The unexplored children of a node are explored and dfs_low(u) is accordingly updated.
- A node is encountered with dfs_low(u) == dfs_num(u) is the first explored node in its strongly connected component and all the nodes above it in the stack are popped out and assigned the appropriate SCC number.
Complexity
- Time complexity: The algorithm is built upon DFS and therefore, each node is visited once and only once. For each node, we perform some constant amount of work and iterate over its adjanceny list. Thus, the complexity is
O(|V|+ |E|) - At maximum, the depth of recursion and the size of stack can be n nodes. Thus the complexity is
O(|V|)
Example
The following figures show the flow of the algorithm on a directed graph with 3 SCCs. Each SCC has been enclosed in a box and the pair (dfs_low(), dfs_num(u)) is mentioned with each node.
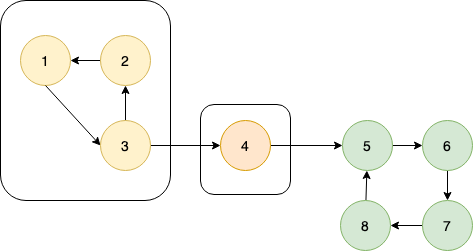 Let us call the tarjan function on node 1.
Let us call the tarjan function on node 1.
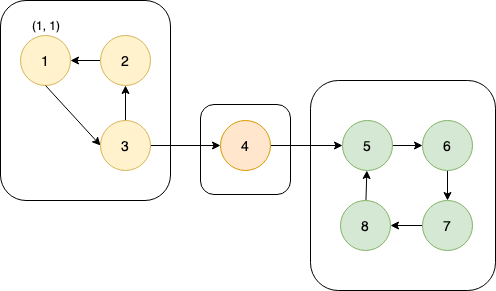 dfs_low[1] and dfs_num[1] are set to 1 & node 1 is pushed to the stack.
dfs_low[1] and dfs_num[1] are set to 1 & node 1 is pushed to the stack.
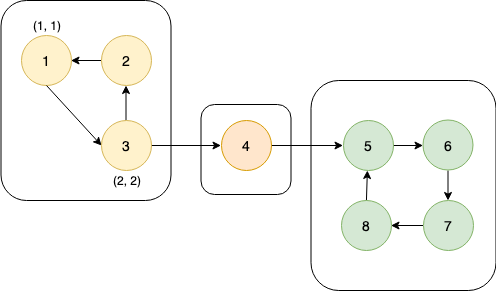 dfs_low[2] and dfs_num[2] are set to 2 and node 2 is pushed to the stack. Let's say that node 4 lies before node 2 in the adjacency list of node 2. So, the function is first called for node 4.
dfs_low[2] and dfs_num[2] are set to 2 and node 2 is pushed to the stack. Let's say that node 4 lies before node 2 in the adjacency list of node 2. So, the function is first called for node 4.
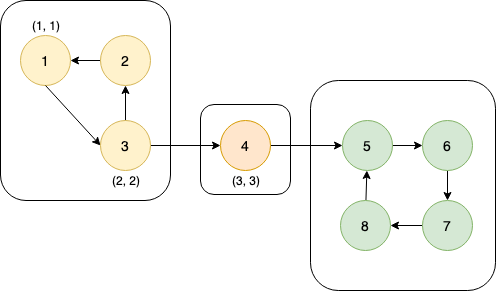 dfs_low[4] and dfs_num[4] are set to 3 & node 4 is pushed to the stack.
dfs_low[4] and dfs_num[4] are set to 3 & node 4 is pushed to the stack.
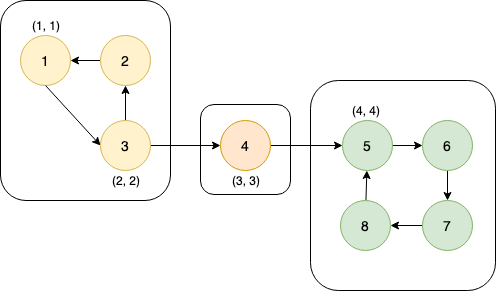 dfs_low[5] and dfs_num[5] are set to 4 & node 5 is pushed to the stack.
dfs_low[5] and dfs_num[5] are set to 4 & node 5 is pushed to the stack.
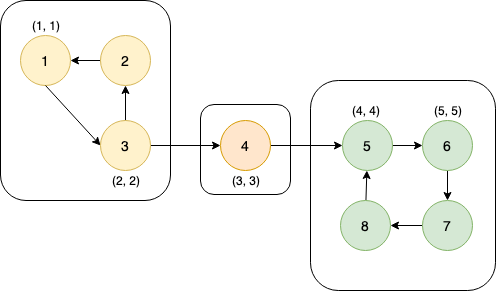 dfs_low[6] and dfs_num[6] are set to 5 & node 6 is pushed to the stack.
dfs_low[6] and dfs_num[6] are set to 5 & node 6 is pushed to the stack.
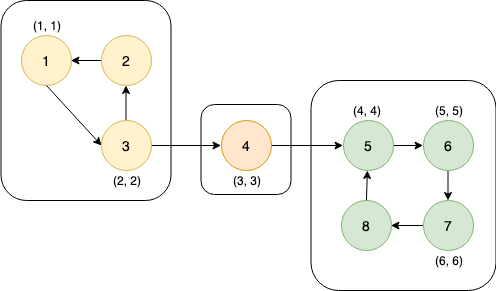 dfs_low[7] and dfs_num[7] are set to 6 & node 7 is pushed to the stack.
dfs_low[7] and dfs_num[7] are set to 6 & node 7 is pushed to the stack.
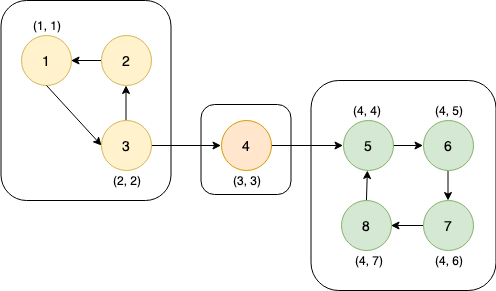 dfs_low[8] and dfs_num[8] are set to 7 & node 8 is pushed to the stack.
Owing to node 5, dfs_low[8] is updated to be 4.
dfs_low[7] is updated to 4.
dfs_low[6] is updated to 4.
For node 5, dfs_low[5] and dfs_num[5] remain the same. So, nodes are popped from the stack until node 5 resulting in-
SCC: 5 8, 7, 6
dfs_low[8] and dfs_num[8] are set to 7 & node 8 is pushed to the stack.
Owing to node 5, dfs_low[8] is updated to be 4.
dfs_low[7] is updated to 4.
dfs_low[6] is updated to 4.
For node 5, dfs_low[5] and dfs_num[5] remain the same. So, nodes are popped from the stack until node 5 resulting in-
SCC: 5 8, 7, 6
For node 4, dfs_low[4] and dfs_num[4] remain the same. So, nodes are popped from the stack until node 4 resulting in-
SCC: 4
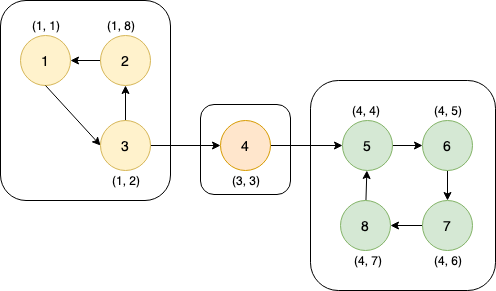
dfs_low[3] and dfs_num[3] are set to 8 & node 3 is pushed to the stack.
Owing to node 1, dfs_low[3] is updated to be 1.
dfs_low[2] is updated to 1.
For node 1, dfs_low[1] and dfs_num[1] remain the same. So, nodes are popped from the stack until node 1 resulting in-
SCC: 1 2, 3
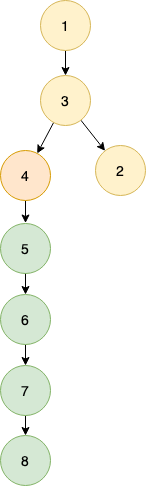
This figure shows the DFS spanning tree of the graph. It can be easily observed that the SCCs form subtrees in the spanning tree.
The output for code for this graph is,
SCC-1-> 5 8, 7, 6,
SCC-2-> 4
SCC-3-> 1 2, 3,
Implementation
- adj_list[NMAX]: Adjacency list for each node
- dfs_num[NMAX]: dfs_num value for each node
- dfs_low[NMAX]: dfs_low value for each node
- SCC[NMAX]: SCC number for each node
- C++
C++
#include<iostream>
#include<stack>
#define NODE 8
using namespace std;
int graph[NODE][NODE] = {
{0, 0, 1, 0, 0, 0, 0, 0},
{1, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 1, 0, 0, 0}
};
int min(int a, int b) {
return (a<b)?a:b;
}
void findComponent(int u, int disc[], int low[], stack<int>&stk, bool stkItem[]) {
static int time = 0;
disc[u] = low[u] = ++time; //inilially discovery time and low value is 1
stk.push(u);
stkItem[u] = true; //flag as u in the stack
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) {
if(disc[v] == -1) { //when v is not visited
findComponent(v, disc, low, stk, stkItem);
low[u] = min(low[u], low[v]);
} else if(stkItem[v]) //when v is in the stack, update low for u
low[u] = min(low[u], disc[v]);
}
}
int poppedItem = 0;
if(low[u] == disc[u]) {
while(stk.top() != u) {
poppedItem = stk.top();
cout << poppedItem << " ";
stkItem[poppedItem] = false; //mark as item is popped
stk.pop();
}
poppedItem = stk.top();
cout << poppedItem <<endl;
stkItem[poppedItem] = false;
stk.pop();
}
}
void strongConComponent() {
int disc[NODE], low[NODE];
bool stkItem[NODE];
stack<int> stk;
for(int i = 0; i<NODE; i++) { //initialize all elements
disc[i] = low[i] = -1;
stkItem[i] = false;
}
for(int i = 0; i<NODE; i++) //initialize all elements
if(disc[i] == -1)
findComponent(i, disc, low, stk, stkItem);
}
int main() {
strongConComponent();
}Applications
The applications of Tarjan's algorithm to find strongly connected components are:
- To converted the graph into a Directed Acyclic Graph of strongly connected components
- For solving 2 SAT problems, where the problem is unsatisfiable if both a variable and its complement lie in the same SCC.
Questions
Question 1: It is possible for two nodes belonging to different SCCs to be reachable from one another.
Question 2: It can be seen in the code that we iterate over the all the nodes and if the corresponding SCC has not been determined yet, we call the 'tarjan' function. During this iteration, is it possible here for a node to not have an assigned SCC no. and another node from its SCC to have it assigned ?
Tarjan's vs Kosaraju's algorithm
While both the methods have a linear time complexity, the techniques for SCC computation are fairly different. Tarjan's method relies on the timestamps of nodes in a DFS to parition the graph whereas Kosaraju's method performs two DFSs on the graph and is somewhat similar to the method for finding the topological sorting.
