
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 5 minutes
Circle sort is a sorting algorithm in which concentric circles are made on array and the elements lying on the same circle diametrically opposite to each other are compared and if the element in left side is found to be greater than that of right side then they are swapped. The above process is repeated in the recursive manner and the array is divided into sub arrays until we get the array of sorted pairs.
It is an unstable, recursive, parallelizable, in place sorting algorithm. It's one of the fastest ways to sort an inverted array with an average time complexity of O(N log N) and space complexity of O(1)
Algorithm
- Consider an array of n elements.
- Compare the first elemment of the array to the last element, then the second element to the last element and so on.
- Then recursively split the array into two sub arrays and repeat the above step until we get the array of single element.
Example
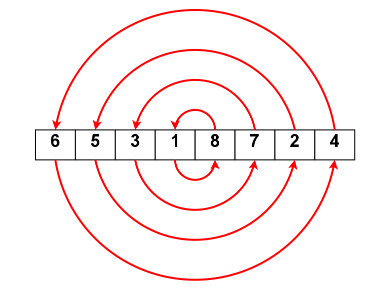
Assume the Unsorted input array is: [6,5,3,1,8,7,2,4].
Based on the above algorithm we first compare the first and the last element and then the second and second the last element and so on until all the elements get compared, and then we divide the array int two sub-arrays and make the same comparison until we get the sorted array.
Step 1: Compare i th element with n-i th element and swap if there are not in the correct order
Step 2: Split the array into two parts of equal size and follow the above step for each part
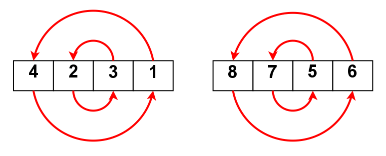
Step 3: Split each part into another two parts and follow the same comparison
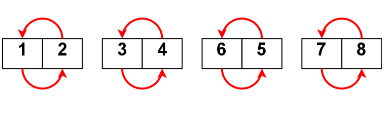
Step 4: On splitting the array into equal parts, each part is of size 1 and hence, we have a sorted array

Implementation
Following code is the C++ implementation of the above algorithm.
#include<bits/stdc++.h>
using namespace std;
bool circleSortRec(int a[], int low, int high)
{
bool swapped = false;
if (low == high)
return false;
int lo = low, hi = high;
while (lo < hi)
{
if (a[lo] > a[hi])
{
swap(a[lo], a[hi]);
swapped = true;
}
lo++;
hi--;
}
if (lo == hi)
if (a[lo] > a[hi + 1])
{
swap(a[low], a[hi+1]);
swapped = true;
}
int mid = (high - low) / 2;
bool firstHalf = circleSortRec(a, low, low+mid);
bool secondHalf = circleSortRec(a, low+mid+1, high);
return swapped || firstHalf || secondHalf;
}
void circleSort(int a[], int n)
{
while (circleSortRec(a, 0, n-1))
{
;
}
}
int main()
{
int a[] = {-1, 5, 15, 2, 12, 44, 60, 8};
int n = sizeof(a)/sizeof(a[0]);
cout<<"\nUnsorted : ";
for (int i=0; i<n; i++)
cout << a[i] << " ";
circleSort(a, n);
cout<<"\nSorted : ";
for (int i=0; i<n; i++)
cout << a[i] << " ";
return 0;
}
Complexity Analysis
-
Best case time complexity: O(N log N)
-
Worst case time complexity: O(N log N log N)
-
Average case time complexity: O(N log N)
-
Space complexity: O(1)
On each step, there will be N comparisons and it will continue till each part has size 1 which will require log N splitting steps. Hence, the overall complexity is O(N log N).
In one go, we get array sorted in two parts. To fix this, we need to run circle sort again. Running circle sort for log N times garentees that the array will be sorted. This is because an element can be at the wrong side atmost log N times as the array is split log N times in each run. Hence, the worst case time complexity will be O(N log N log N)
