KMP (Knuth-Morris-Pratt) Algorithm

Knuth Morris Pratt pattern searching algorithm searches for occurrences of a pattern P within a string S using the key idea that when a mismatch occurs, the pattern P has sufficient information to determine where the next potential match could begin thereby avoiding several unnecessary matching bringing the time complexity to linear.

The algorithm was developed in 1970 by Donald Knuth and Vaughan Pratt.

Given a string S of length n and a pattern P of length m , you have to find all occurences of pattern P in string S provided n > m.

Naive Approach

In naive or brute approach, we check occurence of pattern in string at every poisition i from 1 to n of the string. This approach has time complexity: O(|P| * |S|) or O(m * n). As in the worst case we may check the whole pattern at every possible index of the string. Pseudocode is given below:-

1. result = []
2. for i =: 1 to n - m + 1, do:
3.     for j =: 1 to m, do:
4.         if S[i+j-1] != P[j] : break
5.         else if j == m: result.append(i)

Efficient KMP Algorithm

The main idea behind the efficient approach is that in brute force we have to check every position despite knowing that some positions will never match. So, if we somehow find a way to skip some of the positions that give no useful info we can significantly lower our time used. Before we proceed further we need to know about borders or prefix function.

What is border? Border is the prefix of the string that is equal to its suffix but is not equal to the whole string. That might have been confusing so let us clear the doubts with an example: "ab" is a border of "ab c ab" but it isn't a border of "ab". Here we can see, "ab" is prefix and also a suffix of string "abcab" but we are not considering it a border of string "ab" because the whole string is equal to border. Likewise, "aba" is border of "ababa" but "ab" isn't.

Now, our prefix function just calculate border of maximum length of string S[0....i] for every position i (from 0 to n-1) of string S. How do we calculate that you ask.... Well suppose we already have a string S and its maximum length border. Now, if we append a character in the end it can increase the length of maximum border by 1 at max. Ex. if "aba" is a border of "ababa" and we append "b" to end then new string is "ababab" with border of maximum length 4 as "abab". So for any index i+1 it can have its value of prefix function, f(i+1) < f(i) + 1 . If suppose the border doesn't get increased by 1 we try to find a border smaller than the previous one where it can be increase by 1. If no such border exists then it means this index doesn't form any border yet.

Approach is given below:

1. prefix[] <---- Array of integers to store prefix function values for every index of S.
2. prefix[0] = 0, border = 0
3. for i := 1 to |S| - 1:
4.     while (border > 0) and (S[i] != S[border]) :
5.         border = prefix[border - 1]
6.     if S[i] == S[border] :
7.        border = border + 1
8.     else:
9.         border = 0
10.    prefix[i] = border

Now you may be wondering how this border and prefix function helps us finding the pattern in string. It is clear that our prefix function will have values smaller than the length of the string itself. The next step is a little difficult to comprehend at first but it is the breakthrough. If we see all the values of prefix function and consider only the ones equal to the length of pattern then it means a string of length equal to our pattern is present as prefix and suffix in the string i.e, at every i where prefix[i] = |P| there is a string of length |P| as prefix and suffix in string. What if this string is equal to our pattern P ? Then we only need to look at these positions and voila this is our breakthrough. What we do is construct a new string out of our pattern and string like: (P + "#" + S) where "#" sign is used to append the pattern and string together. We can use any character to append our pattern and string together unless it doesn't appear in both pattern and string. If we calculate prefix function for this string then for every position i where prefix function value is equal to length of pattern, the prefix is our pattern or string before "$" sign and suffix is contained in our string which we have loacted.

1. S = P + # + T <--- here P is pattern and T is text
2. prefix[] = prefix_function(S)
3. result = []
4. for i from |P|+1 to |S|-1:
5.     if prefix[i] = |P|:
6.         result.append(i - 2*|P|)

Complexity

Implementation

#include <bits/stdc++.h>
using namespace std;

void call_prefix(string &kmp, vector<int> &prefix, int len){
    int border = 0;
    for(int i = 1; i < len ;i++){
        while(border > 0 && kmp[i] != kmp[border])
            border = prefix[border - 1];

        if(kmp[i] == kmp[border])
            border++;
        else border = 0;

        prefix[i] = border;
    }
}

int main(){
    string pattern, text;
    cin >>pattern >>text;

    string kmp = pattern + '$' + text;
    int len = kmp.length(), len_of_pat = pattern.length();
    vector<int> prefix(len, 0);

    call_prefix(kmp, prefix, len);
    for(int i = len_of_pat + 1; i < len ;i++){
        if(prefix[i] == len_of_pat)
            cout <<i - 2 * len_of_pat <<" ";
    }
    return 0;
}

Example

1. In below pic upper string is text and lower one is pattern and we search for pattern in text
   
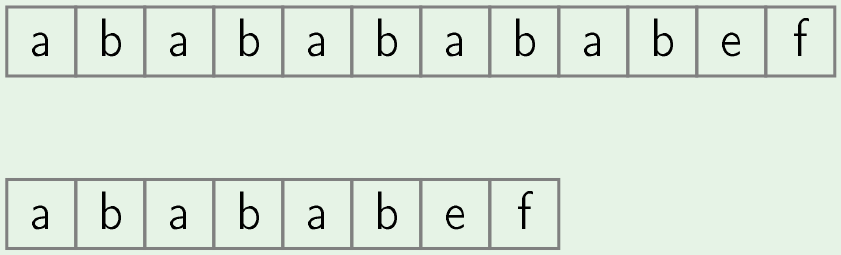
2. In first iteration we check occurence of pattern in text at position 0 and we found that only initial 6 characters of pattern will match.
   
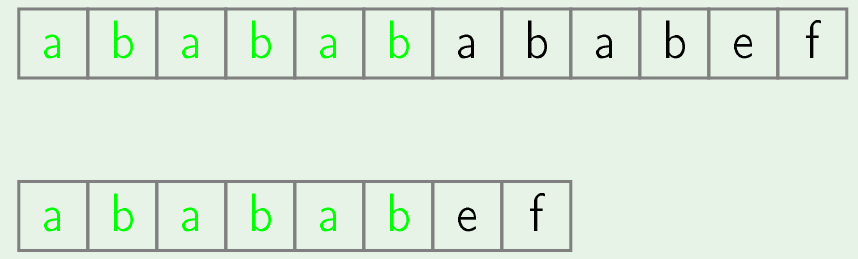
3. Now we will notice that border size of matched string is 4 (i.e "abab").
   
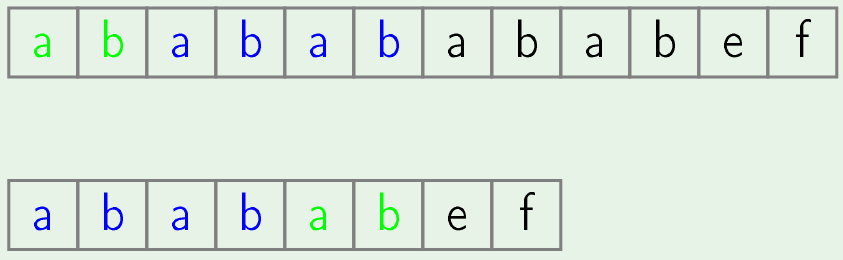
4. Now, we will skip second position of text and in second iteration we just start searching of pattern from 3^rd position of text.
   
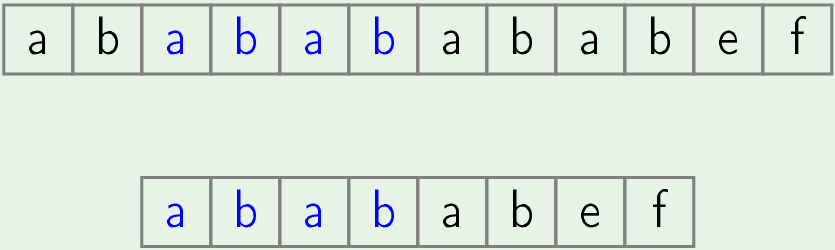
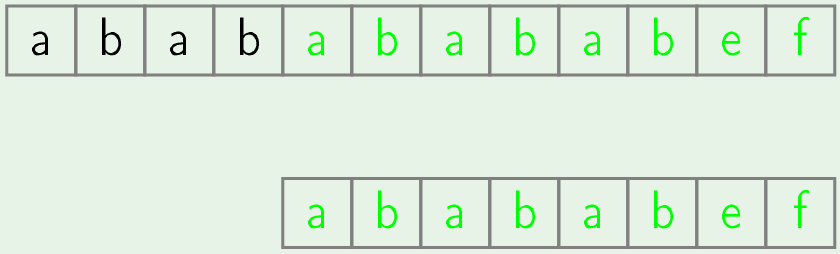
5. Now same process is done for rest of the positions.
   
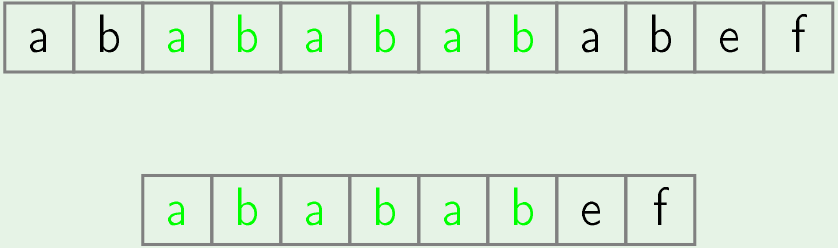
6. finding border for matched string.
   
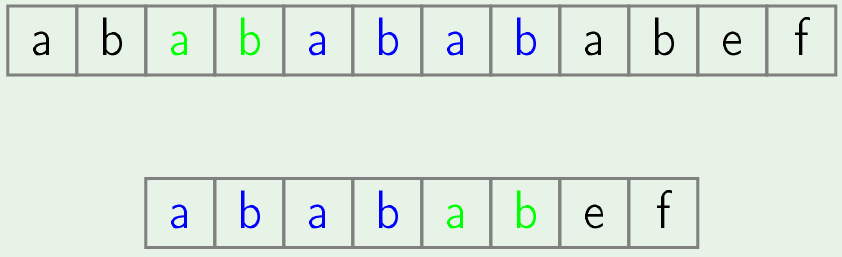
7. Skipping next position.
   
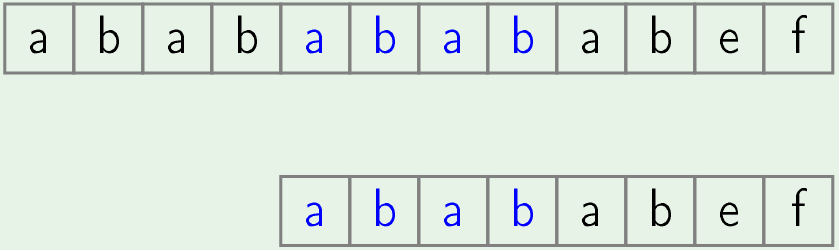
8. Bingo! we found a match at 5^th position.
   

Application

The KMP Algorithm is an efficient exact pattern searching algorithm and is used where fast pattern matching is required but there is a drawback. For differnt patterns and text KMP has to be applied multiple times. So, it is not feasible in case of multiple patterns or texts. In that case, more advanced data structures like: Trie, Suffix Trees or Suffix arrays are used.