In this article, we will cover the basics of lazy code motion in compiler design. This is the idea of reducing redundant calculations or code size, saving resources or other optimizations.

Table of Contents

• Introduction
• Uses
• Redundant Expressions
• Partially Redundant Expressions
• Loop Invariant Expressions
• Example Optimisation
• Limitations
• Conclusion

Pre-requisites:

• Different Code Optimizations in Compiler Design
• Peephole Optimization in Compiler Design

Introduction

In terms of code mobility, optimisations move each calculation across a control-flow graph, a graph which maps the order of execution of a program. This can be done in numerous ways, such as invariant code motion, an optimisation which recognises variables inside loops whose value doesn't change across each iteration, and pulls them outside the loop to avoid unnecessary computations, reducing runtime.

Why is it Useful?

In architecture with a finite and fixed number of registers, a compiler has to allocated its storage for a potentially unlimited number of variables when it is converting intermediate code to machine code. If there are more variables than registers available, some variables will be placed in the stack. Since the stack is located in memory, and memory is slower than CPU registers, placing variables in the stack is expensive in terms of performance. This means that the compiler should aim to minimise the amount of variables that end up in the stack, the exact number of variables which are spilled into the stack depends on whichever optimisation technique is chosen.

In lazy code motion, variables that can be are to be calculated as late as possible, reducing pressure on registers and reducing unnecessary calculations.

Redundant Expressions

Redundant expressions can heavily reduce the runtime of a program. If your code is full of redundancies, you are losing performance in your program that could be gained for free by simply removing these redundancies. In our CFG, an expression is defined as redundant at a point "p" if on each path to p:

• It is evaluated before reaching p
• No constituent value is redefined before p

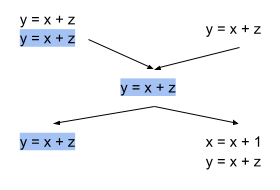
The above graph shows a program with some redundant calculations, we should aim to remove them in all places where they occur to fully optimise our code.

Partially Redundant Expressions

Partially redundant expressions are expressions which fit the rules of redundancy on some but not all paths to p in the CFG.

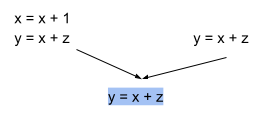
The follow graph contains a redundancy since after the incrementation of x, the expression y = x + z is defined, we can remove this redundancy by removing this expression.

Partially redundancy elimination performs common subexpression elimination and loop-invariant code motion at the same time. It also can perform operation strength reduction which means that PRE is extremely important in compiler opimisation. Furthermore, PRE has been traditionally carried out on lexically equivalent expressions however has more recently been applied to values rather than expressions, which allows for the use of global value numbering in its implementation.

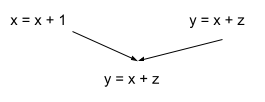
Loop Invariant Expressions

As we touched on in the introduction, another form of lazy code motion is loop invariance. To optimise code in this way, we calculate a variable's value on the first iteration of a loop, if this value does not change with further iterations we know that we can remove it from the loop so that it is only calculated once, reducing computation time.

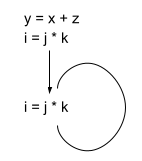
Here we can see that the value of i does not change from iteration to iteration therefore it is partially redundant.

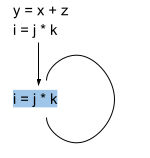
This expression is no longer redundant as we removed the unnecessary calculation of i.

Example Lazy Code Motion Optimisation

if (condition)
{
    //code which does not alter j
    i = j + 1  
}
else
{
    //code which does not alter j
}
k = j + 1

This code is partially redundant as the expression j + 1 is computed twice in a condition controlled loop. To optimise this code, we can use partial redundant elimination through loop-invariant code motion and common subexpression elimination to produce the following optimised code:

if (condition)
{
    //code which does not alter j
    n = j + 1
    i = n
}
else
{
   //code which does not alter j
   n = j + 1
}
k = n

Here, we have removed the redundant assignment and calculation of k = j + 1, instead storing j + 1 inside the temporary variable n and only computed j + 1 once, increasing performance.

Limitations

Expressions that are equal lexically should be placed in the same pseudo-register in optimisation however, adaptations in data-flow analysis may diminish this assumption. To compensate for this, code can be written to ensure that expressions are moved into unique temporary registers. This is okay in practice however it increases pressure on registers and additionally introduce excess move instructions to retrieve these values from the temporary registers.

The computation placement algorithm in lazy code motion is not very efficient. In eager evaluation, the definitions are moved further away from their uses which increases the live range which adds extra pressure to the registers. Lazy evaluation deals with this by moving the variables to a point later in the program where they can be computed later to reduce extra calculations however, this therefore means we have to add basic-blocks onto edges of the CFG which increases overhead. To combat this, basic-block can be merged with its successor or predecessor at an edge in many cases. This will reduce the amount of jumps that have to be made, which could improve performance.

Any pretty-printer in the CFG will not ignore jumps where fall-through would. Although this does not seem particularly important, performance and code size would be both affected negatively, the issues of variable placement and pretty-printers could potentially be solved by running a simplifying pass through after the lazy code motion.

Conclusion

In this article we have covered lazy code motion optimisation techniques. We have given an overview of what this is and why lazy code motion is useful, as well as covering situations where it can be used along with an example optimisation using techniques we have talked about and then finally assessing the limitations of using such methods. After reading you should have a good understanding of the concept and how it used in compiler design.