Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Imagine you had a probelm where you were asked to find the number of unique elements in a list of data where there could be duplicates. There are 2 quick approaches one could quickly come up with. One option is simply to rely on the library's set but often times they have to deal with reisizing their array, deal with collisions, deal with equality checks. The other option would be simply to sort the list of data then simply iterate through the list and gather non-duplicates. Both of these work fine for small amount of data but when there is a large amount of data in the data set then it becomes an unfeasible approach.

Introduction

Illustrated in the problem section is what is known as cardinality, where your goal is to find the number of distinct elements in set of data where duplicates can exist.

The need for a better solution was in need due to the large datasets in Big Data.

Before diving into LogLog, it's best to understand the basis of how LogLog came about.

Simple Counter / FM Sketch

This is the most simplest approach for cadinality where essentially. Essentially you have a bit map and hash the key then with the hash code you would find the first 1 bit starting left to right and then update the corresponding index at that bit. Now imagine, having more than 1 bit map as they will serve as buckets to lower the probability of error.

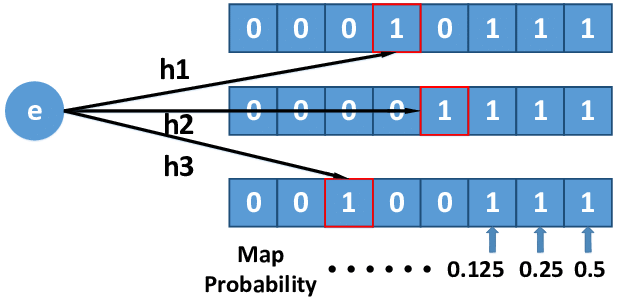
Structure-of-a-FM-Sketch

This is an example of multiple simple counters. By having more counters, the lower the error of cardinality but an increase of memory.

LogLog

Why did I explain what a simple counter was? Essentially, LogLog wanted to minimize the memory needed for multiple simple counters while also minimizing the high error rate that simple counters method had.

Rather than needing multiple simple counters, the LogLog approach allocates enough buckets to store the counts thus reducing the memory needed while also reducing the error rate.

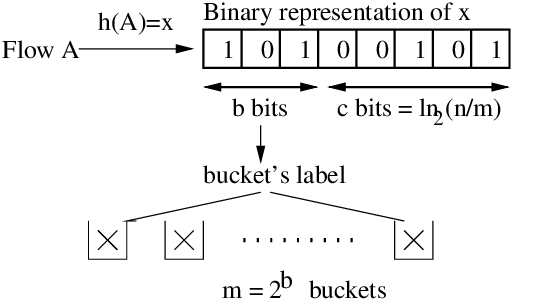
The-stochastic-averaging-process-in-the-HyperLogLog-Algorithm

The idea is to utilize the hash code. The first X bits of the hash code is dedicate towards determining which bucket it belongs to. The bits after the first X bits are dedicated to ranking (giving it a value based on some rank algorithm).

Though not mentioned in most implementations, but 32 bit binary representation is used because it covers most values generated, but for our implementation we will use 64 as that represents a long range.

Lastly, to calculate the cardinality, you would simple sum all the values in the buckets, average that value, then apply it to a stochastic formula.

Probablistic Nature

For most probablistic data structures, it's heavily reliant on a hash function or another means of probablity. As for this LogLog, the hash function will heavily determine the results of cardinality.

If you aren't aware, if the hash function does not properly distribute then lots of collisions will happen. These collisions are not good because this would influence which buckets get selected and what values would be inside of them. This is definitely not what is intendd.

Obviously you should pick a good hash function. Take for example, if you had 1024 buckets, you could estimate 10^8 with a standard error of 4% where each register had 5 bits. Now the math behind this is a bit much to explain, but rather I'll put the original paper of this idea in the resources section for you to look at if you're interested. The paper was written by Marianne Durand and Philippe Flajolet.

Hash Function

Before implementing, you need a very good hash function. Most implementations use Murmur3 Hash which is very good and proven hash function.

This hash function is important for the internals of this data structure, so it's important to select a high quality hash function.

Getting the Bucket Index

Simply you define how many buckets you want, often it's a power of 2 to make numbers nice.

You need to determine how many bits are required to get that bucket number.

This is described in the picture in the LogLog section, where the "b bits" represent bucket bits (the first X bits). Once you know how many bits are required, you get the binary representation of the hash code and you take the first X bits then find the interger value of those bits and make sure it's bounded within the range of 0 to totalBuckets-1.

Ranking

This is described in the picture in the LogLog section, where the "c bits" represent bucket bits (the bits after the first X bits). After getting the bucket index, you will use the remaining bits. Ranking is the term for determining the value that a bucket will have, though definitions are slightly different for different data structures.

One common ranking method is to find the position of the first 1 bit starting left to right using the remaining bits. If unable to find the a 1, return the total numeber of bits then. Once the value and bucket is determined, pick the maximum between the value at the current bucket with the new ranking value.

There are variations on the ranking method so testing a lot is needed to ensure quality results.

This ranking is important because it will serve as the counter which the buckets store. The ranking will be used in calculating the cardinality.

Cardinality

Once you have enough information, the general formula to caluate the cardinality using LogLog is:

Cardinality = gamma function value x number of buckets x 2 ^ averageCount.

Average count is calculated by summing up all the values in the bucket then diving by the number of buckets.

Gamme function is a little complex, so I've given you a sufficent gamma value instead.

Take note, cardinality is not exact but rather an estimation.

Code

import java.util.Arrays;
import java.util.Collection;

public class LogLog<T> {
	public interface Hasher<T> {
		long hash(T obj);
	}

	private int[] counter;
	private Hasher<T> hasher;
	private int neededBucketBits;
	private static final double GAMMA_VALUE = 0.39701;

	public LogLog(Hasher<T> hasher, int numberOfCounters) {
		this.hasher = hasher;
		counter = new int[numberOfCounters];
		neededBucketBits = Integer.toString(numberOfCounters, 2).length();
	}

	public void add(Collection<T> dataset) {
		for (T data : dataset) {
			String binaryForm = getBinaryForm(hasher.hash(data));
			int bucketIndex = Integer.parseInt(binaryForm.substring(0, neededBucketBits), 2) % counter.length;
			int rank = rank(binaryForm.substring(neededBucketBits));
			counter[bucketIndex] = Math.max(counter[bucketIndex], rank);
		}
	}

	private static int rank(String binaryStr) {
		int rank = findLeftmostOneBit(binaryStr);
		return rank != -1 ? rank : binaryStr.length();
	}

	private static String getBinaryForm(long hashcode) {
		return addPadding(Long.toString(hashcode, 2));
	}

	private static String addPadding(String binaryRepresentation) {
		return "0".repeat(64 - binaryRepresentation.length()) + binaryRepresentation;
	}

	private static int findLeftmostOneBit(String binaryStr) {
		return binaryStr.indexOf('1');
	}

	private double averageCount() {
		int sum = 0;
		for (int count : counter) {
			sum += count;
		}
		return sum / (double) counter.length;
	}

	public double cardinality() {
		return GAMMA_VALUE * counter.length * Math.pow(2, averageCount());
	}
}

Here is the full code. I think most of it is rather straight forward.
This application does require you to create a hash function which as suggested before, try to implement the Murmur3 Hash function as it has resulted in good performance for this data structure.

Applications

Useful for whenever you need to find a quick estimate of unique things.
- IP Addresses
- DNA Sequences
- Devices hitting
- Etc

Extension

There is an improvement to LogLog which is known as HyperLogLog. The main idea is the same however calculating the cardinality is different, but has been proven to net better results.

Nonetheless, it is still important to understand the idea of how this came about and how you could modify this idea to fit your needs.

It takes a lot of playing around with and testing such as ranking algorithms, hash functions, buckets, and etc to ensure better results for your application.

LogLog (Probabilistic Data Structure for Cardinality)

Data Structures probabilistic algorithm