
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Lets assume you wanted to find how similar two sets are. You could simply brute force your way by going through the contents of one set and compare those elements with the other set. Sure this method can work but what if you wanted to check a bunch of other sets? This would be rather slow, especially if you are working with a lot of data.
Jaccard Similarity
Some of you may know this equation and how to apply it, so you may skip this section.
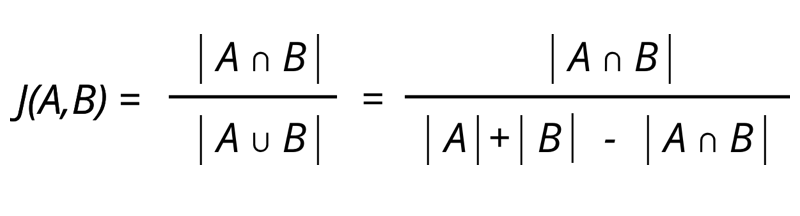
For those that are unfamilar with Jaccard similarity, then this will be important.
You should also know how math with sets, but I'll try my best to explain these operations.
A set is a collection of distinct elements.
- This means each element in the set can only appear once.
- Invalid set: A = { 1, 1, 2, 3, 4, 4, 4, 5}, has duplicate 1's and 4's.
- Valid set: A = { 1, 2, 3, 4, 5 }, has no duplicates
- Valid set: A = { }, empty set
The intersection between two sets results in a set that contains elements both sets A and B share in common.
- Given sets: A = { 1, 2, 3 }, B = { 3, 4, 5 }
- A ∩ B = { 3 }.
The union between two sets is both sets A and B combined together and removing duplicate copies of elements.
- Given sets: A = { 1, 2, 3 }, B = { 3, 4, 5 }
- A ∪ B = { 1, 2, 3, 4, 5 }
The size of a set is the number of elements in a given set denoted by | set | .
- Given set: A = { 1, 2, 3, 4, 5 }
- | A | = 5, because there are 5 elements.
The image above shows the equation of how to calculate the Jaccard similarity which is a numeric score to compare similarity between two sets.
The equation states that you need to calculate the size of the intersection between A and B then divide by the size of the union of A and B. This equation can be translated into the size of the intersection between A and B divided by size of A plus size of B minus the interersection between A and B.
Using the information above, you could work out simple sets to determine the Jaccard similarity number.
The problem stated at the beginning of the article briefly covered the idea of finding Jaccard similarity but rather in an obscure way, but nonetheless trying to find the exact value is too time consuming.
MinHash
MinHash was originally an algorithm to quickly estimate the jaccard similarity between two sets but can be designed as a data structure that revolves around the algorithm. This is a probablistic data structure that quickly estimates how similar two sets are.
The idea behind MinHash is representing each set as a signature. A signature preserves a permutation of a bit array representation of a set. By using hash functions that simulate a permutation, the probability of collisions against all permutations results to the Jaccard similarity.
This is hard to grasp, so I will walk you through what is happening.
Probablistic Nature
The probablistic nature behind this data structure is purely through the hash functions in the signature matrix. You will get a better understanding when you walk through the steps, but for now bare with me. The has functions in the signature matrix determine the performance of the data structure.
Not having enough hash functions will cause small amount of comparisons to properly gauge similarity between two sets due to all the values probably colliding. However, it's essential to create/use high quality distributed hash algorithms (could look them up) as it's unlikely to have a similar value during similarity comparison time. The more high quality hash functions you have, the better the evaluation of similarity will result, but there is a threshold, so you have to test your results and see.
Regardless, a hash function is the pivotal part needed but there aren't enough out there as you may want a lot. If you need more hash functions then you could use 1 hash function and go through the process of salting, which is basically rehashing a hash code over and over. Or you could create your own way to manipulate the hash code through proper bit manipulation but salting is a very easy and efficient solution. These salted hash codes would still result be good enough to act as a hash function that hashed those values.
Despite having quick performance, since hash functions are limited to a certain range of values and collisions are bound to happen, the similarity is not always accurate. I can't fully explain the error rate, however in the resource section, the L5-Minhash link has a more in-depth answer also Wikipedia states the true error rate.
This was a lot of information, the most important thing to note is that good hash functions are pivotal in the performance of this data structure as are most probablistic data structures.
What the process looks like
So what exactly does the MinHash data structure do? Well it's an algorithm but can be converted into a data structure and I will explain the process of creating it.

Above is the picture of the steps needed for the data structure to work. If you get confused, I will explain more in-depth the following sections.
- Get a collection of sets then create an input matrix known which are just rows of bit arrays.
- This bit arrays will be the length of the universal set size (the total number of unique values).
- Create a signature matrix filled with max value.
- Iterate through the input matrix and whenever you see a non-zero value, find the corresponding set it bit belongs to and pass index value through the set of hash functions in the signature matrix and take the minimum value.
Step 1) Building each bit array representation
The initial step is to build a bit array for each set, however we need to know how big to make it. In order to do so, you need to know the universal set size which is the size of the union of all sets that will be used later to compare.
Lets assume we have 3 sets
- A = { 1, 3, 5, 7 }
- B = { 0, 2, 8, 10 }
- C = { 4, 5, 6, 8, 9, 10 }
- Universal Set ( A ∪ B ∪ C ) = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }
Since the size of the universal set is 11, we will make each bit array size 11. Then you will go through each element in a set and get the hash code then bound that hash code with the total size of the universal set. Once you find the bounded hash code, you will represent that element as present denoting it a value that is not 0, such as 1.
In this case, let's assume the hash code of a number is the number itself. This would result in bit arrays:
- Bit array A = [0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0 ]
- Bit array B = [1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1 ]
- Bit array C = [0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1 ]
Universal Set Size
private int getUniversalSetSize(Set<T>... sets) {
Set<T> universalSet = new HashSet<>();
for (Set<T> set : sets) {
universalSet.addAll(set);
}
return universalSet.size();
}
The code above is an example of how one might find the universal size of all sets unioned together.
Building Bit Arrays
private int[][] buildBinaryDocSet(Set<T>... sets) {
int[][] binaryDocSet = new int[sets.length][totalFeatures()];
for (int setIdx = 0; setIdx < sets.length; setIdx++) {
for (T feature : sets[setIdx]) {
binaryDocSet[setIdx][bound(feature.hashCode())] = 1;
}
}
return binaryDocSet;
}
We are simply iterating through each set and updating the bit array to represent out set.
- totalFeatures() is the universal set size.
- bound(hashcode) is simply hashcode % universal set size
Step 2 Building the Signature Matrix
After building the bit array representations, this is where minhash matrix is built.
Rows of the matrix are denoted by a hash function.
Columns of the matrix are denoted by the sets indices.
private int[][] buildSignatureMatrix() {
int[][] sigMatrix = initSigMatrix();
for (int feature = 0; feature < totalFeatures(); feature++) {
for (int document = 0; document < totalDocuments(); document++) {
if (binaryDocSet[document][feature] != 0) {
computeSigHashes(sigMatrix, document, feature);
}
}
}
return sigMatrix;
}
To clarify:
- feature and features refers to elements of a set
- document refers to a specific index of a set.
The idea behind this method is to go through each bit array and whenever we see a non-zero value, we will update our signature matrix calling computeSigHashes function.
It's important to initialize the matrix with all maxiumum values because we will be calling Math.min function to preserve the property of a signature matrix.
private void computeSigHashes(int[][] sigMatrix, int document, int feature) {
for (int hasher = 0; hasher < totalHashFunctions(); hasher++) {
sigMatrix[hasher][document] = Math.min(sigMatrix[hasher][document], bound(hashers[hasher].hash(feature)));
}
}
Go through each hash function and the associated set index and then select the minimum value between the current value in the signature matrix and the bounded hashed index.
Similarities
After building the signature table, calculating an estimate of the Jaccard similarty will be easy.
public double similarity(int docIndex1, int docIndex2) {
int similar = 0;
for (int hasher = 0; hasher < totalHashFunctions(); hasher++) {
if (signatureMatrix[hasher][docIndex1] == signatureMatrix[hasher][docIndex2]) {
similar++;
}
}
return (double) similar / totalHashFunctions();
}
Go down each row of the matrix and compare the set index for both. If they have the same value, increment a running count.
Lastly, divide the running count by the total rows (aka total number of hash functions).
Code
Here is the full code of all the segments, I have renamed some of the terms because originally this algorithm was developed for web searches but has since then found other applications.
import java.util.Arrays;
import java.util.HashSet;
import java.util.Set;
public class MinHash<T> {
public interface Hasher {
int hash(int item);
}
private int totalFeatures;
private int[][] binaryDocSet;
private int[][] signatureMatrix;
private Hasher[] hashers;
@SafeVarargs
public MinHash(Hasher[] hashers, Set<T>... sets) {
this.hashers = hashers;
totalFeatures = getUniversalSetSize(sets);
binaryDocSet = buildBinaryDocSet(sets);
signatureMatrix = buildSignatureMatrix();
}
@SafeVarargs
private int getUniversalSetSize(Set<T>... sets) {
Set<T> universalSet = new HashSet<>();
for (Set<T> set : sets) {
universalSet.addAll(set);
}
return universalSet.size();
}
//Better to store in a sparse matrix
@SafeVarargs
private int[][] buildBinaryDocSet(Set<T>... sets) {
int[][] binaryDocSet = new int[sets.length][totalFeatures()];
for (int setIdx = 0; setIdx < sets.length; setIdx++) {
for (T feature : sets[setIdx]) {
binaryDocSet[setIdx][bound(feature.hashCode())] = 1;
}
}
return binaryDocSet;
}
private int[][] buildSignatureMatrix() {
int[][] sigMatrix = initSigMatrix();
for (int feature = 0; feature < totalFeatures(); feature++) {
for (int document = 0; document < totalDocuments(); document++) {
if (binaryDocSet[document][feature] != 0) {
computeSigHashes(sigMatrix, document, feature);
}
}
}
return sigMatrix;
}
private int[][] initSigMatrix() {
int[][] sigMatrix = new int[totalHashFunctions()][totalDocuments()];
for (int[] vector : sigMatrix) {
Arrays.fill(vector, Integer.MAX_VALUE);
}
return sigMatrix;
}
private void computeSigHashes(int[][] sigMatrix, int document, int feature) {
for (int hasher = 0; hasher < totalHashFunctions(); hasher++) {
sigMatrix[hasher][document] = Math.min(sigMatrix[hasher][document], bound(hashers[hasher].hash(feature)));
}
}
public double similarity(int docIndex1, int docIndex2) {
int similar = 0;
for (int hasher = 0; hasher < totalHashFunctions(); hasher++) {
if (signatureMatrix[hasher][docIndex1] == signatureMatrix[hasher][docIndex2]) {
similar++;
}
}
return (double) similar / totalHashFunctions();
}
private int bound(int hash) {
return hash % totalFeatures();
}
public int totalFeatures() {
return totalFeatures;
}
public int totalDocuments() {
return binaryDocSet.length;
}
public int totalHashFunctions() {
return hashers.length;
}
public static void main(String[] arsgs) {
Hasher h1 = num -> (22 * num + 5) % 31;
Hasher h2 = num -> (30 * num + 2) % 31;
Hasher h3 = num -> (21 * num + 23) % 31;
Hasher h4 = num -> (15 * num + 6) % 31;
Hasher[] hashers = { h1, h2, h3, h4 };
Set<Integer> doc1 = new HashSet<>(Arrays.asList(8, 15, 16));
Set<Integer> doc2 = new HashSet<>(Arrays.asList(1, 5, 7, 10, 11, 15, 16, 17));
Set<Integer> doc3 = new HashSet<>(Arrays.asList(0, 1, 2, 3, 4, 5, 7, 9, 12, 17));
Set<Integer> doc4 = new HashSet<>(Arrays.asList(1, 5, 6, 13, 14, 15));
Set<Integer> doc5 = new HashSet<>(Arrays.asList(1, 2, 5, 9, 13, 15, 18));
MinHash<Integer> minhash = new MinHash<>(hashers, doc1, doc2, doc3, doc4, doc5);
System.out.println(minhash.similarity(1, 2)); //doc2, doc3
System.out.println(minhash.similarity(3, 4)); //doc4, doc5
System.out.println(minhash.similarity(0, 2)); //doc1, doc3
}
}
This code shows you an example of sets usings numbers from 0 through 18.
Pros and Cons
- The minhash similarity number is an estimate of the Jaccard similarity, so sometimes there is a margin of error.
- MinHash has many different variations such as B-bit which uses bits to save a good amount of memory rather than using purely arrays of ints while still preserving easy implementation.
- The more refined quality hash functions that you provide, the less the error of similarity will be but at the cost of more memory.
- You must define your own permutation hash functions which means you need to have an understanding of how quality hash functions are created.
- Often a prime number is involved.
Applications
- Near-duplicates detection
- Search industry, machine learning systems, content matching, and etc.
