
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Algorithm
Complexity
Implementations
Questions
Merge sort is a fast comparison based sorting algorithm which can be utilized in sorting a Linked List as well. Merge Sort is preferred for sorting a linked list. The slow random-access performance of a linked list makes some other algorithms such as Quick Sort perform poorly, and others such as Heap Sort completely impossible.
Algorithm
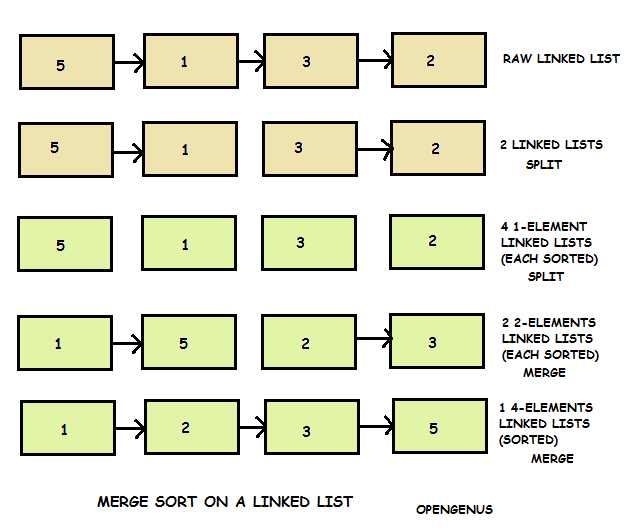
The algorithm is same as that of Merge Sort will implementation changes to accomodate the structure of Linked List.
Pseudocode
Merge_Sort(head_reference)
STEP 1: If head is NULL or there is only one element in the Linked List
then return the Linked List
STEP 2: Divide the linked list into two equal halves.
Split_Linked_List(head, &first_half, &second_half);
STEP 3: Sort the two halves first_half and second_half.
MergeSort(first_half);
MergeSort(second_half);
STEP 4: Merge the sorted first_half and second_half (using Merge_Sort() recursively)
and update the head pointer using head_reference.
*head_reference = Merge_Sort(first_half, second_half);
Complexity
- Worst case time complexity:
Θ(N log N) - Average case time complexity:
Θ(N log N) - Best case time complexity:
Θ(N log N) - Space complexity:
Θ(1)
Implementations
Implementation of applying Merge Sort on a Linked List is as follows:
- C
- Java
C
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next;
};
struct Node* SortedMerge(struct Node* a, struct Node* b);
void FrontBackSplit(struct Node* source, struct Node** frontRef, struct Node** backRef);
void MergeSort(struct Node** headRef)
{
struct Node* head = *headRef;
struct Node* a;
struct Node* b;
if ((head == NULL) || (head->next == NULL))
{
return;
}
FrontBackSplit(head, &a, &b);
MergeSort(&a);
MergeSort(&b);
*headRef = SortedMerge(a, b);
}
struct Node* SortedMerge(struct Node* a, struct Node* b)
{
struct Node* result = NULL;
if (a == NULL)
return(b);
else if (b==NULL)
return(a);
if (a->data <= b->data)
{
result = a;
result->next = SortedMerge(a->next, b);
}
else
{
result = b;
result->next = SortedMerge(a, b->next);
}
return(result);
}
void FrontBackSplit(struct Node* source, struct Node** frontRef, struct Node** backRef)
{
struct Node* fast;
struct Node* slow;
slow = source;
fast = source->next;
while (fast != NULL)
{
fast = fast->next;
if (fast != NULL)
{
slow = slow->next;
fast = fast->next;
}
}
* frontRef = source;
* backRef = slow->next;
slow->next = NULL;
}
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node = (struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
int main()
{
struct Node* res = NULL;
struct Node* a = NULL;
push(&a, 3);
push(&a, 1);
push(&a, 2);
MergeSort(&a);
getchar();
return 0;
}
Java
public class linkedList
{
node head = null;
static class node
{
int val;
node next;
public node(int val)
{
this.val = val;
}
}
node sortedMerge(node a, node b)
{
node result = null;
if (a == null)
return b;
if (b == null)
return a;
if (a.val <= b.val)
{
result = a;
result.next = sortedMerge(a.next, b);
}
else
{
result = b;
result.next = sortedMerge(a, b.next);
}
return result;
}
node mergeSort(node h)
{
if (h == null || h.next == null)
{
return h;
}
node middle = getMiddle(h);
node nextofmiddle = middle.next;
middle.next = null;
node left = mergeSort(h);
node right = mergeSort(nextofmiddle);
node sortedlist = sortedMerge(left, right);
return sortedlist;
}
node getMiddle(node h)
{
//Base case
if (h == null)
return h;
node fastptr = h.next;
node slowptr = h;
while (fastptr != null)
{
fastptr = fastptr.next;
if(fastptr!=null)
{
slowptr = slowptr.next;
fastptr=fastptr.next;
}
}
return slowptr;
}
void push(int new_data)
{
node new_node = new node(new_data);
new_node.next = head;
head = new_node;
}
public static void main(String[] args)
{
linkedList li = new linkedList();
li.push(3);
li.push(2);
li.push(1);
li.head = li.mergeSort(li.head);
}
}
Questions
What is the time complexity of this algorithm if Linked List is already sorted?
O(N)
O(1)
O(N log N)
O(log N)
