In this article at OpenGenus, we will learn how to design and implement Merge Sort in C++ Programming Language in detail using OOP concepts.

Definition:

Merge Sort is a sorting algorithm that sorts an array of elements using the Divide-and-Conquer approach. To create a sorted array, the algorithm splits the array in two, sorts each half individually, and then merges the two halves back together.

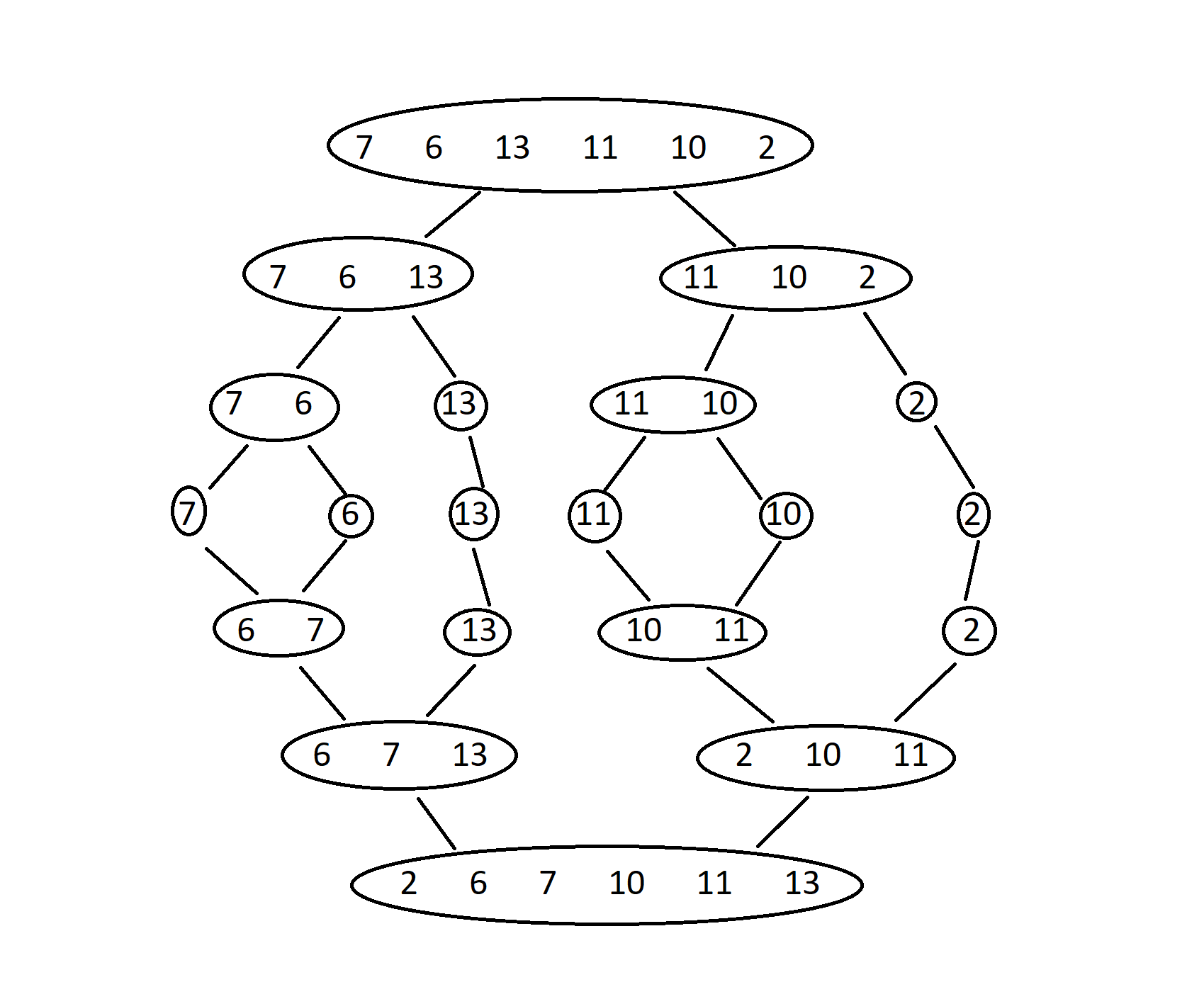
Figure showing the recursive Merge Sort

Algorithm:

Merge Sort is a Divide and Conquer Algorithm.

Steps to perform the Merge Sort:

• We will divide the given unsorted array into two halves of equal size.
• Then, we will recursively sort the first and second half.
• After sorting two halves, we will merge them to get the required sorted array.

Implementation of the Merge Sort Algorithm using Object-Oriented Programming(OOP):

In this implementation, the MergeSort class contains a public member function, mergeSort and a private member function, merge.

The merge() function is specified as private member function in the merge sort implementation because they are only used within the MergeSort class. This function carry out the fundamental operation of the merge sort algorithm, but because they are not visible to outside callers, they are not concerned with the algorithm's inner working.

On the other hand, a merge sort implementation uses a public member function to offer an interface for calling the sorting algorithm from outside code. Because it is the function that external code will call to sort an array of integers, the mergeSort() function in the MergeSort class is specified as a public member function.

Following is the structure of the MergeSort Class:

class MergeSort{

    public: 
    void mergeSort{
        //array is divided into two halves and sorted recursively
    }
    
    private:
    void merge{
        //two sorted halves gets merge into a single sorted array
    }
};

From the point of user, we can use this class as follows:

    MergeSort mSort;
    mSort.mergeSort(arr, 0, n-1);

The mergeSort() function first divides the array into two halves and then recursively sorts them and calls the merge() function. When the base case of a single element is reached, the two halves are merged together using the private merge() function. The merge() function is a helper function that merges two sorted sub-arrays.

We use a vector temp in the implementation of merge sort in C++ because it provides several advantages such as:

• Vectors in C++ are dynamic arrays that can be resized at runtime and it is useful for merge sort because the size of the input array can vary depending on the input data.
• It is safer to use because they automatically handle memory allocation and deallocation.
• It also supports random access, which means that we can access any element in the array in constant time.

class MergeSort
{
    public:
    void mergeSort(int arr[], int l, int r)
    {    
        //l and r are the starting and ending index of the unsorted array
        if(l >= r) return;
        
        //mid is the index which divides the array into two almost equal halves 
        int mid = (l+r)/2;
        
        //to sort the left half
        mergeSort(arr, l, mid);
        
        //to sort the right half
        mergeSort(arr, mid+1, r);
        
        //to merge the two sorted halves
        merge(arr,l,mid,r);
    }
    
    private:
    void merge(int arr[], int l, int m, int r)
    {
         int left = l;
         int right = m+1;
         
         //to store the sorted elements
         vector<int> temp; 
         
         while(left <= m && right <= r){
             if(arr[left] <= arr[right]){
                 temp.push_back(arr[left]);
                 left++;
             }else{
                 temp.push_back(arr[right]);
                 right++;
             }
         }
         while(left <= m){
             temp.push_back(arr[left]);
             left++;
         }
         while(right <= r){
             temp.push_back(arr[right]);
             right++;
         }
         for(int i = l;i <= r;i++){
             arr[i] = temp[i-l];
         }
    }
    
};

int main(){
    int n;
    cin>>n;

    int arr[n];

    for(int i = 0;i < n;i++){
        cin>>arr[i];
    }

    MergeSort mSort;
    mSort.mergeSort(arr, 0, n-1);

    for(int i = 0;i < n;i++){
        cout<<arr[i]<<" ";
    }
    return 0;
}

Output:

    6
    7 6 13 11 10 2  //Unsorted array
    2 6 7 10 11 13  //Sorted array

Time Complexity:

The divide step takes O(logn) time, since the array is divided into halves recursively until there is only one element in each sub-array. The merge step takes O(n) time, since each element of the array is compared and merged into a new array.

• Best Case Complexity - It occurs when the array is already sorted. The best-case time complexity of merge sort is O(n*logn).
• Average Case Complexity - It occurs when the array elements are neither arranged in ascending nor descending order. The average case time complexity of merge sort is O(n*logn).
• Worst Case Complexity - It occurs when the array elements are in descending order. The worst-case time complexity of merge sort is O(n*logn).

Space Complexity:

In Merge Sort algorithm, during merging, we create a temporary array to store the two sorted halves.
Therefore, the space complexity of Merge Sort is O(n), where n is the number of elements in the array being sorted.

With this article at OpenGenus, you must have the complete idea of how to implement Merge Sort in C++ Programming Language.