
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 5 minutes
A Fibonacci series is one in which every number is the sum of previous 2 numbers appearing in the series. The series goes something like: 0 1 1 2 3 5 8 13 21...
A number Fn, where n is the index of said number in the series is defined as Fn=Fn-1 + Fn-2 for n>1 and the starting 2 terms of the series are fixed to F0=0, F1=1.
Fibonacci numbers find various uses in mathematics and computing so often that many a times these may go unnoticed. The fibonacci series finds applications in algorithms like Fibonacci search technique, the Fibonacci heap data structure, graphs called Fibonacci cubes which are used to interconnect parallel & distributed systems
Dynamic Programming
Dynamic programming is a specialized optimization technique that finds its applications in both mathematics as well as computing. It works on the principle of dividing the problem into smaller subproblems and recursively combining their solutions to obain the overall solution. Our aim is to simplify a problem by breaking it down recursively till the point we can't divide it any further. Any problem that can be solved by dividing in this manner and using the solutions of subproblems t build upto the final solutions is said to have an optimal substructure.
This method was concieved by Richard Bellman in the year 1950 and has since then found applications in various fields ranging from engineering, computation to even economics. A very large number of computational algorithms are known to use dynamic programming and some optimized through the use of the same.
In this article we shall discuss one of the simpler applications and implementation of dynamic programming, which is to find the nth Fibonacci number in the series. This method improves heavily on the recursive search by eliminating the need for heavy resource usage of the system stack and slowdown visible especially with larger indices.
Algorithm
Let the index of our required number be n.
In order to determine the number in fibonacci sequence at nth position, we simply follow the premise:
Fn = Fn-1 + Fn-2
For dynamic programming method, we need to store the previous series somewhere to arrive at the required Fn.
We make use of an array to perform our task.
Length of the array: n(Since we begin indexing from 0).
Now,
F0 = 0
F1 = 1
And for every position 'x' in the array, Fx = Fx-1 + Fx-2
So,
F2 = F1 + F0 = 1 + 0 = 1
F3 = F2 + F1 = 1 + 1 = 2
And so on.
Example
Let us take an example of 7th number in the series.
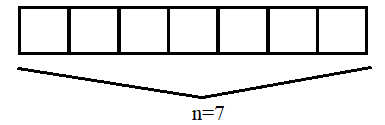
We now have, n=7
In order to find the 7th number, we need to create an array of length n in order to store the entire series, since we begin from 0.
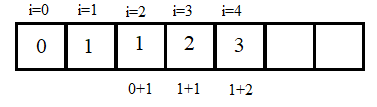
We now store every result a sum of values in prevous 2 indices.
We get the last number from the array, which is our required result.
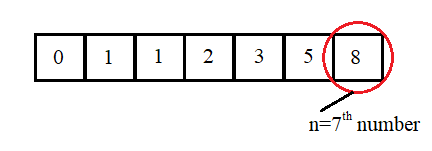
Thus, we divided this problem of the nth number into n subproblems for numbers at every index and used the result of each in order to arrive at our final solution.
Pseudocode
function FibonacciNumber(index n):
/*Create array of required length*/
integer array FibArray[n+1]
FibArray[0]=0
FibArray[1]=1
/*Loop over the array and calculate the numbers at all positions*/
for(i=2 to n+1)
FibArray[i]=FibArray[i-1]+FibArray[i-2]
return FibArray[n+1]
Implementation
- C
- C++
- Java
- Python
C
//Function creates an array with specified length and returns the last element as nth Fibonacci number
int fibonacciNumber(int n){
int fibArray[n],i;
fibArray[0] = 0, fibArray[1] = 1;
for(i=0; i<n; i++)
fibArray[i] = fibArray[i-1]+fibArray[i-2];
return fibArray[n-1];
}
//The parameters in bracket may be ignored
//They are used to input command line arguments and are not necessary
int main(int argc, char* argv){
int n;
printf("Which number in series do you want?");
scanf("%d", &n);
printf(fibonacciNumber(n));
return 0;
}
C++
//Function creates an array with specified length and returns the last element as nth Fibonacci number
int fibonacciNumber(int n){
int fibArray[n],i;
fibArray[0] = 0, fibArray[1] = 1;
for(i=0; i<n; i++)
fibArray[i] = fibArray[i-1]+fibArray[i-2];
return fibArray[n-1];
}
//The parameters in bracket may be ignored
//They are used to input command line arguments and are not necessary
int main(int argc, char* argv){
int n;
cout<<"Which number in series do you want?";
cin>>n;
cout<<fibonacciNumber(n);
return 0;
}
Java
//class used for user input
import java.util.Scanner
class fibonacciNumber{
//Function to create an array with specified length and returns the last element as nth Fibonacci number
protected int fib(int n){
int fibArray[n],i;
fibArray[0] = 0, fibArray[1] = 1;
for(i=0; i<n; i++)
fibArray[i] = fibArray[i-1]+fibArray[i-2];
return fibArray[n-1];
}
}
//The main class used to run the program
public class mainClass{
public static void main(String[] args){
//create objects for the class to access their contents
Scanner sc = new Scanner(System.in);
fibonacciNumber f = new fibonacciNumber();
System.out.println("Which number in series do you want?");
int n = sc.nextInt();
System.out.println(f.fib(n));
}
}
Python
#Function to create an array with specified length and returns the last element as nth Fibonacci number
def fibbonaciNumber(n):
fibArray = []
fibArray.append(0)
fibArray.append(1)
if n>1:
fibArray.append((fibArray[i-1]+fibArray[i-2]) for i in range(2,n))
return fibArray[n-1]
print(fibbonaciNumber(input('Which number in series do you want?')))
Space Optimization
The above solution stores all the previous numbers into the memory despite the fact that we need only the last number from this array. However, having to manually delete every element from our array just increases the time complexity of our program and is not efficient. We instead have another way, where we only make use of the last 2 results and replace the previous ones repeatedly with these. In this method, we do not have the requirement of an array to store our problem and instead simply calculate our solution in the same way as before with only the previous 2 numbers present everytime.
Pseudocode:
function FibonacciNumber(index n):
/*Store first 2 values of the sequence*/
integer FibonacciFirst = 0, FibonacciSecond = 1, FibonacciResult
/*Loop for n+1 times and replace the first and second with values in the next indices*/
for(i=2 to n+1)
FibonacciResult = FibonacciFirst + FibonacciSecond
FibonacciFirst = FibonacciSecond
FibonacciSecond = FibonacciResult
return FibonacciResult
Implementation:
- C
- C++
- Java
- Python
C
//Function repeatedly iterates over the series till the specifed point
int fibonacciNumber(int n){
int i, fibonacciFirst = 0, fibonacciSecond = 1, fibonacciResult;
if(n == 0)
return fibonacciFirst;
else if(n == 1)
return fibonacciSecond;
else
for(i=0; i<n; i++){
fibonacciResult = fibonacciFirst + fibonacciSecond;
fibonacciFirst = fibonacciSecond;
fibonacciSecond = fibonacciResult;
}
return fibonacciResult;
}
//The parameters in bracket may be ignored
//They are used to input command line arguments and are not necessary
int main(int argc, char* argv){
int n;
printf("Which number in series do you want?");
scanf("%d", &n);
printf(fibonacciNumber(n));
return 0;
}
C++
//Function repeatedly iterates over the series till the specifed point
int fibonacciNumber(int n){
int i, fibonacciFirst = 0, fibonacciSecond = 1, fibonacciResult;
if(n == 0)
return fibonacciFirst;
else if(n == 1)
return fibonacciSecond;
else
for(i=0; i<n; i++){
fibonacciResult = fibonacciFirst + fibonacciSecond;
fibonacciFirst = fibonacciSecond;
fibonacciSecond = fibonacciResult;
}
return fibonacciResult;
}
//The parameters in bracket may be ignored
//They are used to input command line arguments and are not necessary
int main(int argc, char* argv){
int n;
cout<<"Which number in series do you want?";
cin>>n;
cout<<fibonacciNumber(n);
return 0;
}
Java
class fibonacciNumber{
//Function repeatedly iterates over the series till the specifed point
protected int fib(int n){
int i, fibonacciFirst = 0, fibonacciSecond = 1, fibonacciResult;
if(n == 0)
return fibonacciFirst;
else if(n == 1)
return fibonacciSecond;
else
for(i=0; i<n; i++){
fibonacciResult = fibonacciFirst + fibonacciSecond;
fibonacciFirst = fibonacciSecond;
fibonacciSecond = fibonacciResult;
}
return fibonacciResult;
}
}
//The main class used to run the program
public class mainClass{
public static void main(String[] args){
//create objects for the class to access their contents
Scanner sc = new Scanner(System.in);
fibonacciNumber f = new fibonacciNumber();
System.out.println("Which number in series do you want?");
int n = sc.nextInt();
System.out.println(f.fib(n));
}
}
Python
#Function repeatedly iterates over the series till the specifed point
def fibbonaciNumber(n):
fibonacciFirst, fibonacciSecond = 1,2
if n == 1:
return fibonacciFirst
elif n == 2:
return fibonacciSecond
else:
for _ in range (n-2):
fibonacciResult = fibonacciFirst + fibonacciSecond
fibonacciFirst = fibonacciSecond
fibonacciSecond = fibonacciResult
return fibonacciResult
print(fibbonaciNumber(input('Which number in series do you want?')))
Complexity
- Worst case time complexity:
Θ(n) - Average case time complexity:
Θ(n) - Best case time complexity:
Θ(n) - Space complexity:
Θ(n) - Space optimized complexity:
Θ(1)
Applications
- Used in charting analysis (technical analysis) in stock trading along with trend lines and candlestick graphs.
- Conversion of miles to km(consecutive digits represent the nearest rounded value with left digit as miles and right as kilometres).
- Fibonacci cubes used for interconnecting parallel & distributed systems.
- Fibonacci heap data structure
- Fibonacci search technique
