Number of ordered pairs such that (A[i] & A[j])=0

Reading time: 30 minutes | Coding time: 10 minutes

Given an array A[] of n integers, find out the number of ordered pairs such that (A[i]&A[j])=0,where 0<=(i,j)<n.Here,we are considering (i,j) and (j,i) to be different.There are some constraints in this problem: 1<=n<=10^4 and 1<=A[i]<=10^4. We can either go about it by brute-forcing through all possible pairs which will require a lot of time and calculations i.e. about O(n^2) or we can make use of dynamic programming to break this down into smaller sub-problems and use the result of each to build up to our solution.

To understand the dynamic programming approach let's just first learn some of the basic concepts.

Bitwise AND set of a number n

Bitwise AND set of a number n is all posssible numbers i smaller than or equal to n such that (n&i) is equal to i.So,here we can say i will be a bitwise subset of mask n if (n&i)==i.

Example:

Input : n=9
Output : 0,1,8,9
Explanation : 0&9=0
              1&9=1
              2&9=0
              3&9=1
              4&9=0
              5&9=1
              6&9=0
              7&9=1
              8&9=8
              9&9=9

Method

In the dynamic programming approach, we use a hash table(hash[])to count the occurrence of every element.Here,key observations are the constraints,the maximum that an array element can be is 10^4,so calculating the mask upto 2^15 will be enough.We will take a 2d-array dp[][], where the row represents the mask and the column represents the bit-no(bit-no of last bit will be considered as 0).We will iterate over 15 bits(let it be N) only because maximum mask value posssible is 2^15.dp[mask][i] will store the number of subsets of mask which differ from mask in first i bits.

For calculating number of subsets of a particular mask,

Let's consider the i-th bit to be 0,then no subset can differ from the mask in the i-th bit as it would mean that the numbers will have a 1 at the i-th bit where the mask has a 0 which would mean that it is not a subset of the mask.So,we can conclude that the numbers now differ in the first (i-1) bits only.Hence,

dp[mask][i] = dp[mask][i-1]

Let's consider the i-th bit to be 1,then it can be divided into two non-intersecting sets.One set containing numbers with i-th bit as 1 and differing the mask in the next (i-1) bits,another set containing numbers with i-th bit as 0 differing from mask(xor)(2^i) in next (i-1) bits.Hence,

dp[mask][i] = dp[mask][i-1] + dp[mask (xor) (2^i)][i-1]

Talking about base case or when i=0(talking about last bit):

• If the last bit is 0:

dp[mask][0] = hash[mask]

• If the last bit is 1:

dp[mask][0] = hash[mask] + hash[mask (xor) 1]

We perform the above task for each possible mask.

Let's see how we can fill the dp array with the help of psuedocode:

 Let N=15
 create a hash table and store the occurrences of the element.
 create a dp array, dp[1<<N][N+1]
 initialize dp with 0.
 for(mask=0 to (1<<N)){
     if(mask&1)
         dp[mask][0]=hash[mask]+hash[mask^1]      //If the last bit is 1
     else
         dp[mask][0]=hash[mask]                   //If the last bit is 0
    for(i=1 to N+1){
       if(mask&(1<<i))
         dp[mask][i]=dp[mask][i-1]+dp[mask^(1<<i)][i-1]//If mask's i-th bit is 1
       else
         dp[mask][i]=dp[mask][i-1]    //If mask's i-th bit is 0
    }
}

ALgorithm

1. Create a 2d-array dp[][] and store the number of subsets of mask(present in the given array)which differ from mask in first i bits for each mask(as explained above).

2. Create a variable ans and for every array element add the number of subsets dp[temp][15] to ans,where temp is the complement of the given array element.
   here,temp=((1<<15)-1)(xor)A[i].

3. Return ans.

Explanation of addition of dp[temp][15]:

As we know complement of a number gives 0 on applying bitwise & operator.So,obviously subset of the complement will also return 0.

Let's take an example:

Suppose A[i]=5 in binary it is 101.Suppose N=3 in this case,now reverse of 101 is 010 which on applying bitwise & gives 0.So,(1<<3) gives 1000 which on subtraction from 1 gives 111.111(xor)101 gives 010 which is the reversed bit.So,we can conclude that dp[temp][15] will have the number of subsets that returns 0 on applying bitwise & operator.

Implementation

 #include<bits/stdc++.h>
 using namespace std;

 const int N=15;

 //Function to count pairs
 long long count(int A[],int n){
      unordered_map<int,int> hash;
      long long dp[1<<N][N];

      //Initialize dp to 0
      for(int i=0;i<(1<<N);i++){
          for(int j=0;j<N;j++){
              dp[i][j]=0;
          }
      }

      //Count the frequency of every element
      for(int i=0;i<n;i++){
          hash[A[i]]+=1;
      }

      //Iterate for all possible values that A[i] can take
      for(long long mask=0; mask<(1<<N); mask++){
          //If the last bit is 1
          if(mask&1){
              dp[mask][0]=hash[mask]+hash[mask^1];
          }else{
              //If the last bit is 0
              dp[mask][0]=hash[mask];
          }

          for(int i=1;i<N;i++){
              //If mask's i-th bit is 1
              if(mask&(1<<i)){
                  dp[mask][i]= dp[mask][i-1]+dp[mask^(1<<i)][i-1];
              }else{
              //If mask's i-th bit is 0
                  dp[mask][i]=dp[mask][i-1];
              }
         }
    }

    //Count the number of pairs
    long long ans=0;
    for(int i=0;i<n;i++){
        ans+=dp[((1<<N)-1) ^ A[i]][N-1];
    }

    return ans;
}

int main(){
   int A[]={3,4,2};
   int n=3;
   cout<<count(A,n)<<endl;
   return 0;
}

Output:

4

Example

Input : A[]={3,4,2}
Output : 4
Explanation:
Here,maximum element present in the array is 4,which can be represented in 3-bit so,we will take N=3 and iterate over the mask only till 2^3(just for the sake of calculation).

hash table :

    3 - 1
    4 - 1
    2 - 1

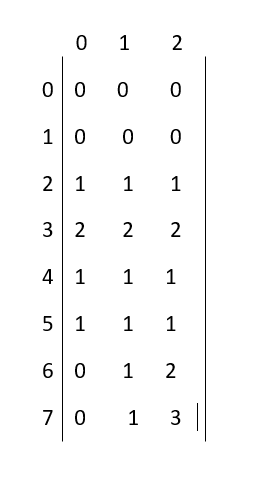
dp array:

evaluating ans:

ans=0;
i=0 -> dp[4][3]  ; ans+=1
i=1 -> dp[3][3]  ; ans+=2
i=2 -> dp[5][3]  ; ans+=1

Hence,ans=4.

Complexity

• Time Complexity : O(N.(2^N)) where N is the maximum number of bits possible
  here,N=15

• Space Complexity : O(N.(2^N))