Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
The problem states that given a number or a score, we need to find the number of ways to reach it using increments of 1 and 2 with a constraint that consecutive 2s aren't allowed. We will solve this using Dynamic Programming in linear time O(N).
Consider the example
4
1+1+1+1
1+2+1
1+1+2
2+1+1
Note: Consecutive 2s does not imply that we can't use more than two 2s in forming the number, the number of 2s aren't restricted, only the order is. As long as they don't swing together that is fine.
Check out this example. For 5 the possible ways are
1+1+1+1+1
2+1+2
2+1+1+1
1+2+1+1
1+1+2+1
1+1+1+2
In this article we'll be discussing two approaches to solve this problem
- Brute Force O(2^N) time and O(1) space
- Dynamic Programming O(N) time and O(N) space
Brute Force approach
The logic here is actually very simple, we can run a recursive algorithm. What we'll be doing is maintain a boolean variable, say, flag, this flag will have the information if a 2 was previously used to get the score or no. And then by having a basic conditional statement we can call our function.
Let's call the function count(). It takes two parameters the target, call it 'n' and flag. And the return variable for this method will be res, which returns the number of ways we can reach a score or a number using 1 and 2, no consecutive 2s allowed. The res variable is initialized to 0, at the beginning of the method.
The main logic is as follows
if (!flag && n > 1)
res= res + count(n - 1, false) + count(n - 2, true);
else
res = res + count(n - 1, false);
flag=false indicates that we haven't used 2 yet and flag=true represents vice versa.
For the if statement we are checking whether flag is false and n is still greater than zero.
If yes, then we call the function twice
1.count(n-1,false) implies we are taking one step at a time and since we are not using 2 here, the flag still remains false.
2 count(n-2,true) implies we are taking two steps or moves at a time. Also this time flag becomes true since we are using 2.
The else loop is when we've already used 2, thus, using only 1 this time.
Implementation for the above logic:
#include<iostream>
using namespace std;
int count(int n, bool flag){
if(n==0) return 1;
int res=0;
if(flag==false && n>0){
res = res + count(n-1, false) + count(n-2, true);
}
else {
res = res + count(n-1,false);
}
return res;
}
int main(){
cout<<count(4,false);
}
Output
4
How the algorithm works?
The core logic has been explained above. This is a recursive algorithm, hence it is a top down approach, which means, that we will be starting at our score and we will keep reducing it to a point where it either becomes 0, which means that there is a path or a possibility of forming the score with given numbers, in this case, it is 1 and 2 or the score becomes negative which states that the path we've chosen can't fetch us the score.
According to this basic criteria we write our code. As mentioned earlier we always start flag with false(flag as boolean is something that we've taken, of course you could swap the false with true or use something else altogether, like a counter with binary values) and in the count() we code our base conditions like n=0. The rest goes as explained.
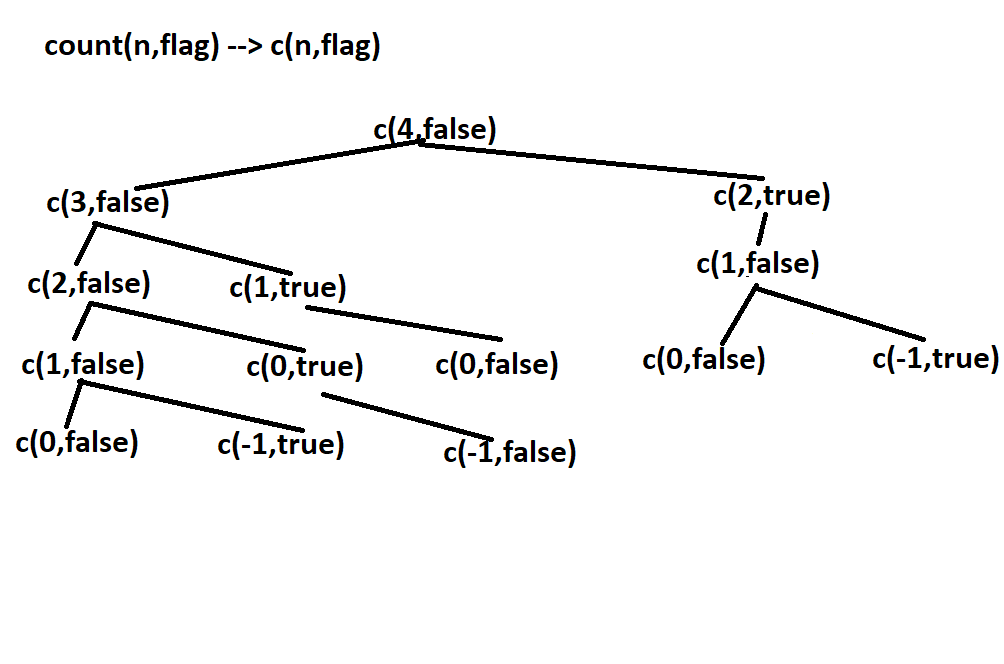
From the above figure we can say that some subproblems have been called more than once, which obviously increases the computational time.
This problem has optimal substructure property as the problem can be solved using solutions to subproblems. To get an optimal solution we employ dynamic programming.
Dynamic Programming approach
This approach will be very similar to the brute force approach. The main drawback of the brute force was the fact that the optimal substructure wasn't handled very well. Therefore we will be introducing a 2D array to store our intermediate results. We're taking a 2D array because we have two crucial variables, which is, the current n value and current flag value. The logic is same, even the procedure except, in this approach we store our res values in a 2D array.
Let's call the array dp[][], the maximum number of rows the dp can hold is 'n+1' and columns is 2, which is, 0 or 1, depending on the flag value.
The idea is as follows:
dp[i][0] = Number of ways to form i by considering both 1 and 2 as the last element
dp[i][1] = Number of ways to form i by considering 1 as the last element
Due to this structure, the recursive relation becomes:
dp[i][0] = dp[i-1][0] + dp[i-2][1]
This is because:
- On taking 2, the remaining value is i-2 and we cannot have consecutive 2s so the DP value is dp[i-2][1]
Another structure is as follows:
dp[i][1] += dp[i-1][0]
as we have the option to consider 1 only.
Let's see the code first.
#include<iostream>
using namespace std;
int count(int n, int flag){
if(dp[n][flag]!=-1)
return dp[n][flag];
if(n==0) return 1;
int res=0;
if(flag==0 && n>0){
res = res + count(n-1, 0) + count(n-2, 1);
}
else {
res = res + count(n-1,0);
}
return dp[n][flag]=res;
}
int main(){
int n=4;
int dp[n+1][2];
memeset(dp,-1,sizeof(dp));
cout<<count(n,0);
}
Output
4
What the algorithm does?
The dp[][] basically maintains the state of subproblems, as this is still a recursive algorithm, it is a top down approach which means the subproblems will be further divided into subproblems, but the array will be filled from the beginning index i.e 0. Initially all the values of the dp will be -1, which is also the base case in the count(), implies that any of the subproblems haven't been visited or calculated yet. Once a subproblem will be visited, its value based on the current n value and the flag value will be updated, after solving the subproblems that are below the hierarchy of the current one.The rest logic is the same.
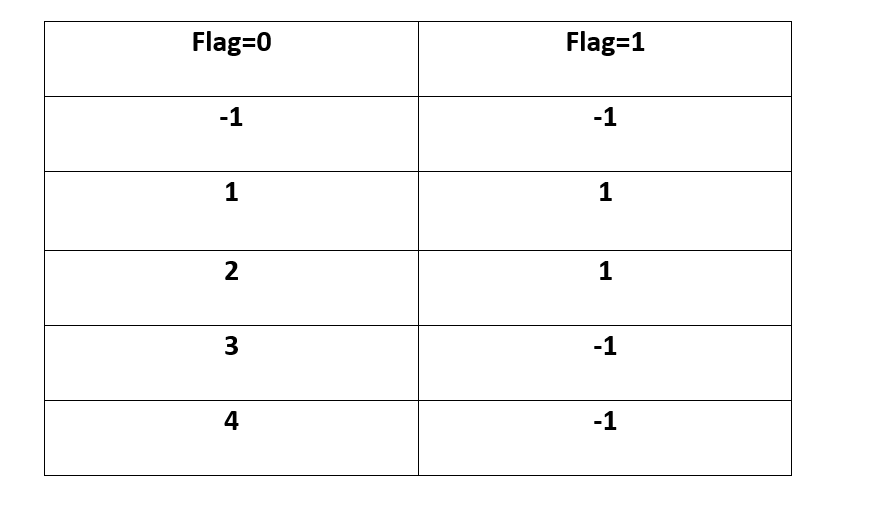
The dp[][] for n=4 will be
The rows represent the current n value, the column represent the flag value. column=0 represnts that flag is 0 which means that a 2 has't seen before and similar for column=1.
Although the value of n=4 we took the number of rows as 5, because there is no such score as 0. Also, any state that hasn't been visited during the process will be -1. Example of such a state is dp[4][1], remember, we started the count() with n=4 and flag=0. The values in the matrix aren't the number of times count(4,0) was called, it is the result of count(4,0) which in turn is the result of count(3,0)+count(2,1). At the end count(4,0) which is dp[4][0] will contain the result.
You can once refer the figure under the brute force approach, the matrix will be clear for you.
Time Complexity.
Unlike the previous time complexity, we have achieved a better linear O(n) time complexity.
Talking about space complexity, which is O(N) where N is our target score/number. Generally a 2D array takes up row * column space, since our coulmns will always be 2, we can take that as a constant.
How does adding a constraint on the consecutive 2s differ when compared to not adding?
- The basic idea of both the problems are the same. Given a score how many ways are there to reach it, adding the constraint does change how we see the problem, by adding a constraint we are considering the same sequence of numbers with different orders unlike the previous one where we simply ignored that solution. 1. In this version of the problem (1,2,1),(1,1,2),(2,1,1) are different, but, in the original statement all the three solutions are the same. This is due to the fact that, in the previous one, it really didn't matter if the 2s are together or not, but, since we now have the constraint we are exploring all the options thoroughly.
- The approach is also quite different, in this version we are using the top down recursive approach with a memoisation table, in the previous one, we implied a simple bottom up approach, counting the increments.
- Talking about the time complexities the time and the space taken by both the algorithms is the same.
Applications
- This problem in many ways is similar to the famous "Coin Change problem", one of the important problems to understand dynamic programming.
- Dynamic Programming in general has found to be very useful in optimization problems.
Question
Why the value of column is always 2
With this article at OpenGenus, you must have the complete idea of solving this challenging problem of finding the number of ways to reach a number using increments of 1 and 2 (consecutive 2s are not allowed).