
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 20 minutes
Octree is a tree data structure where each internal node has 8 children. An octree is generally used to represent relation between objects in a 3-dimensional space. It is used in 3D computer graphics. Octrees are also used for nearest neighbor search which can be done easily in logarithmic time.
Like a binary tree divides a 1-dimensional space into two segments, an octree subdivides the 3D space into 8 octants where each octant is represented by a node.
An octree save a large amount of space when storing points in a 3D space, especially if the space is sparsely populated. If there are k points in a 3D cube of dimension N, then space used by the tree is O(klog2N)
The image below shows how an octree represents points in a space.
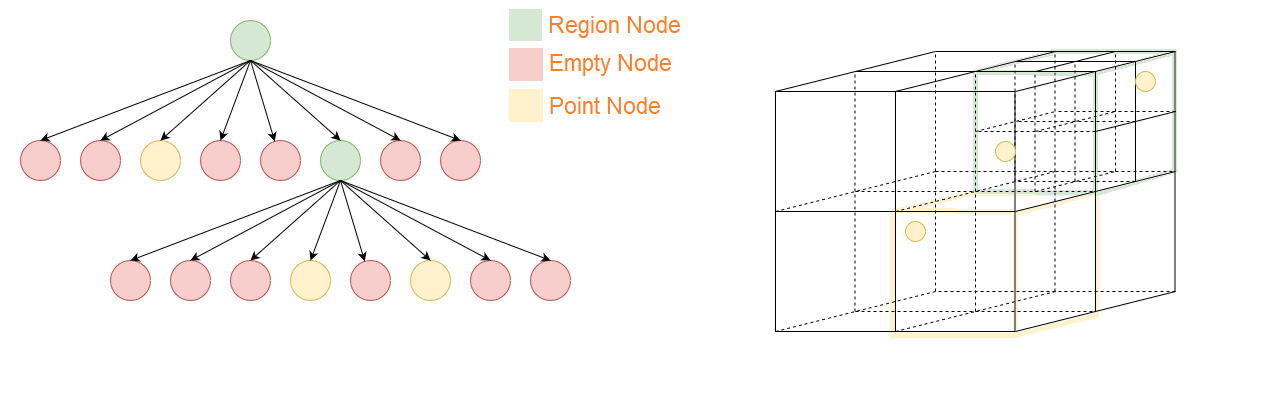
Algorithm
-
Three types of nodes are used in octree:
- Point node: Used to represent of a point. Is always a leaf node.
- Empty node: Used as a leaf node to represent that no point exists in the region it represent.
- Region node: This is always an internal node. It is used to represent a 3D region or a cuboid.
A region node always have 4 children nodes that can either be a point node or empty node.
Insertion
- Insertion: This is a recursive function used to store a point in the octree.
1. Start with root node as current node.
2. If the given point is not in cuboid represented by current node, stop insertion
with error.
3. Determine the appropriate child node to store the point.
4. If the child node is empty node, replace it with a point node representing the
point. Stop insertion.
5. If the child node is a point node, replace it with a region node. Call insert for
the point that just got replaced. Set current node as the newly formed region
node.
6. If selected child node is a region node, set the child node as current node.
Goto step 2.Search
- Search: This is a boolean function used to determine weather a point exists in 3D space or not.
1. Start with root node as current node.
2. If the given point is not in boundary represented by current node, stop search
with error.
3. Determine the appropriate child node to store the point.
4. If the child node is empty node, return FALSE.
5. If the child node is a point node and it matches the given point return
TRUE, otherwise return FALSE.
6. If the child node is a region node, set current node as the child region node.
Goto step 2.Note that a 3D cuboid can be represented by 2 points of any of its diagonal.
Complexity
- Time complexity:
- Find: O(log2N)
- Insert: O(log2N)
- Search: O(log2N)
- Space complexity: O(k log2N)
Where k is count of points in the space and space is of dimension N x M x O, N >= M, O.
Implementations
C++ 11
/*
* Code for an octree that demonstrates insertion and search
*/
#include <iostream>
#include <vector>
#define TLF 0 // top left front
#define TRF 1 // top right front
#define BRF 2 // bottom right front
#define BLF 3 // bottom left front
#define TLB 4 // top left back
#define TRB 5 // top right back
#define BRB 6 // bottom right back
#define BLB 7 // bottom left back
struct Point{
int x;
int y;
int z;
Point() : x(-1), y(-1), z(-1) {}
Point(int a, int b, int c) : x(a), y(b), z(c) {}
};
class Octree{
// if point == NULL, node is regional.
// if point == (-1, -1, -1), node is empty.
Point *point;
Point *top_left_front, *bottom_right_back; // represents the space.
std::vector<Octree *> children;
public:
Octree(){
// to declare empty node
point = new Point();
}
Octree(int x, int y, int z){
// to declare point node
point = new Point(x, y, z);
}
Octree(int x1, int y1, int z1, int x2, int y2, int z2){
if(x2 < x1 || y2 < y1 || z2 < z1)
return;
point = nullptr;
top_left_front = new Point(x1, y1, z1);
bottom_right_back = new Point(x2, y2, z2);
children.assign(8, nullptr);
for(int i = TLF; i <= BLB; ++i)
children[i] = new Octree();
}
void insert(int x, int y, int z){
if(x < top_left_front->x || x > bottom_right_back->x
|| y < top_left_front->y || y > bottom_right_back->y
|| z < top_left_front->z || z > bottom_right_back->z)
return;
int midx = (top_left_front->x + bottom_right_back->x) >> 1,
midy = (top_left_front->y + bottom_right_back->y) >> 1,
midz = (top_left_front->z + bottom_right_back->z) >> 1;
int pos = -1;
if(x <= midx){
if(y <= midy){
if(z <= midz)
pos = TLF;
else
pos = TLB;
}
else{
if(z <= midz)
pos = BLF;
else
pos = BLB;
}
}
else{
if(y <= midy){
if(z <= midz)
pos = TRF;
else
pos = TRB;
}
else{
if(z <= midz)
pos = BRF;
else
pos = BRB;
}
}
if(children[pos]->point == nullptr){
// if region node
children[pos]->insert(x, y, z);
return;
}
else if(children[pos]->point->x == -1){
// if empty node
delete children[pos];
children[pos] = new Octree(x, y, z);
return;
}
else{
int x_ = children[pos]->point->x,
y_ = children[pos]->point->y,
z_ = children[pos]->point->z;
delete children[pos];
children[pos] = nullptr;
if(pos == TLF){
children[pos] = new Octree(top_left_front->x, top_left_front->y, top_left_front->z,
midx, midy, midz);
}
else if(pos == TRF){
children[pos] = new Octree(midx + 1, top_left_front->y, top_left_front->z,
bottom_right_back->x, midy, midz);
}
else if(pos == BRF){
children[pos] = new Octree(midx + 1, midy + 1, top_left_front->z,
bottom_right_back->x, bottom_right_back->y, midz);
}
else if(pos == BLF){
children[pos] = new Octree(top_left_front->x, midy + 1, top_left_front->z,
midx, bottom_right_back->y, midz);
}
else if(pos == TLB){
children[pos] = new Octree(top_left_front->x, top_left_front->y, midz + 1,
midx, midy, bottom_right_back->z);
}
else if(pos == TRB){
children[pos] = new Octree(midx + 1, top_left_front->y, midz + 1,
bottom_right_back->x, midy, bottom_right_back->z);
}
else if(pos == BRB){
children[pos] = new Octree(midx + 1, midy + 1, midz + 1,
bottom_right_back->x, bottom_right_back->y, bottom_right_back->z);
}
else if(pos == BLB){
children[pos] = new Octree(top_left_front->x, midy + 1, midz + 1,
midx, bottom_right_back->y, bottom_right_back->z);
}
children[pos]->insert(x_, y_, z_);
children[pos]->insert(x, y, z);
}
}
bool find(int x, int y, int z){
if(x < top_left_front->x || x > bottom_right_back->x
|| y < top_left_front->y || y > bottom_right_back->y
|| z < top_left_front->z || z > bottom_right_back->z)
return 0;
int midx = (top_left_front->x + bottom_right_back->x) >> 1,
midy = (top_left_front->y + bottom_right_back->y) >> 1,
midz = (top_left_front->z + bottom_right_back->z) >> 1;
int pos = -1;
if(x <= midx){
if(y <= midy){
if(z <= midz)
pos = TLF;
else
pos = TLB;
}
else{
if(z <= midz)
pos = BLF;
else
pos = BLB;
}
}
else{
if(y <= midy){
if(z <= midz)
pos = TRF;
else
pos = TRB;
}
else{
if(z <= midz)
pos = BRF;
else
pos = BRB;
}
}
if(children[pos]->point == nullptr){
// if region node
return children[pos]->find(x, y, z);
}
else if(children[pos]->point->x == -1){
// if empty node
return 0;
}
else{
if(x == children[pos]->point->x && y == children[pos]->point->y
&& z == children[pos]->point->z)
return 1;
}
return 0;
}
};
int main() {
Octree tree(1, 1, 1, 4, 4, 4);
std::cout << "Insert (3, 3, 3)\n";
tree.insert(3, 3, 3);
std::cout << "Insert (3, 3, 4)\n";
tree.insert(3, 3, 4);
std::cout << "Find (3, 3, 3):\n";
std::cout << (tree.find(3, 3, 3) ? "True\n" : "False\n");
std::cout << "Find (3, 4, 4):\n";
std::cout << (tree.find(3, 4, 4) ? "True\n" : "False\n");
std::cout << "Insert (3, 4, 4)\n";
tree.insert(3, 4, 4);
std::cout << "Find (3, 4, 4):\n";
std::cout << (tree.find(3, 4, 4) ? "True\n" : "False\n");
return 0;
}Applications
- Used extensively in 3D computer graphics, especially game design.
- Used for triangle search. Paper.
- Used to find closest object in 3D space efficiently.
References/ Further reading
- Youtube video by DevDept Software showing how octree subdivides a 3d mesh.
