Palindromic Tree (Eertree)

Reading time: 30 minutes | Coding time: 15 minutes

A palindromic tree keeps track of all palindromic substrings of a string in linear time and space. The actual structure of palindromic tree is that of a directed graph rather than a tree. The nodes of a palindromic tree store palindromic substrings.

There are 2 types of edges:

• Labeled edges: This is a directed edge that faces downwards. It has some character as its label. A lebeled edge with label a from node u to node v means that node v can be obtained by adding a as a prefix and suffix to substring of u. This makes it possible to obtaing a palindromic substring by traversing down from empty string node.

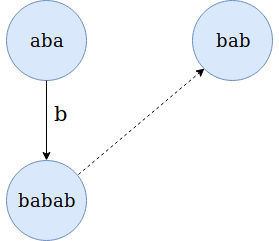
• Suffix edges: These edges points to the node that represents longest proper suffix of the node that is also a palindrome. Every node has exactly one such edge.

Palindromic tree actually has 2 roots:

• first root represents a string of length -1, i.e. an imaginary string. Following a labeled edge from this root adds only the single character that is in label. For example, following the edge with label a from this root will give the string 'a'.

• Second root is a string with length 0, i.e. an empty string. Labeled edge performs normally on this node.

Since a string of length N can have maximum N palindromic substrings, it is guranteed that max nodes in the tree will be N + 2, after including the roots. Max suffix edges will be N, one for every node.

Algorithm

Initializing the tree

• Initializing the tree:
  • Initialize the tree by creating the two roots. Call the root with -1 string length as root1 and root with length 0 as root2. The suffix edge of root1 will point to itself and suffix edge of root2 will point to root1.

Inserting in the tree

• Inserting in the tree:
  • A recursive definition is used to define insertions into the tree. Assume that palindromes of a string S with length l is to be stored in the tree and everything has been stored till an index x. Inserting the character at position x+1 means that a new node will be inserted that will representing longest palindromic substring ending at x+1. So to do that, we need to find the longest substring s which was added on insertion of S[x].
  • Since the suffix edges have also been stored until now, they can be traversed to get to the nodes with all possible candidates for string s efficiently. Start from previously inserted node and keep traversing up through the suffix edges until suitable node is reached. Call this node which stores s as X. Add a labeled edge from X to a new node that stores the string S[x+1]sS[x+1], call it X'.
  • Now we need to add a suffix edge for node X'. To do that, traverse up from node X through the suffix edges till a node is reached that forms a palindrome after adding S[x+1]. The nodes with length 1 will point to root2.

The palindromic substring count problem can be solved just by counting the nodes in the tree. The code can be modified to keep a counter.
Any other problems like counting some sub-palindrome's occourances can be done by simply traversing the tree.

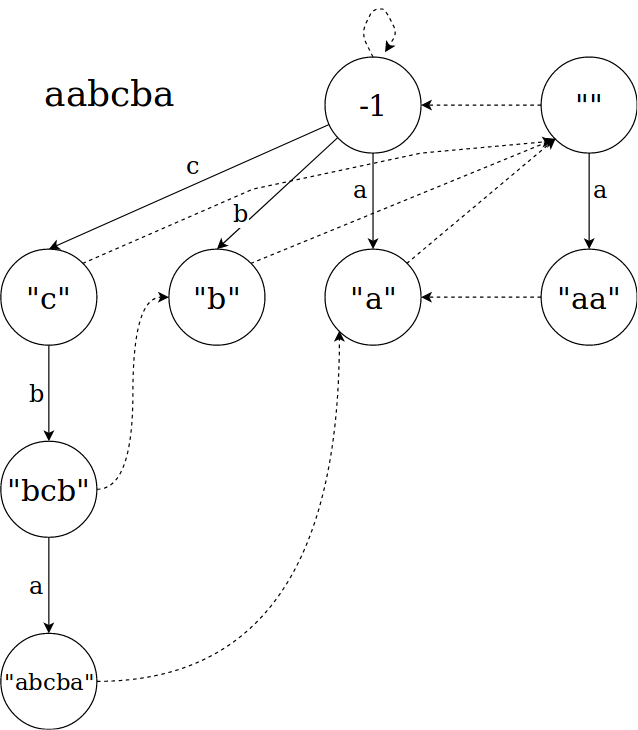
A eertree for the string "aabcba" will look like:

Complexity

• Time complexity:
  1. Build: O(N)
  2. Insert: O(N)
  3. Search: O(N)
• Space complexity: O(N)

Where N is the length of string.

Implementation

C++ 11

/*
 * c++ 11 code to construct an EerTree tree. The method printAll
 * will print all strings stored in the tree.
 */
#include <iostream>
#include <vector>
#include <string>

struct Node{
    int start, end;
    int len;

    Node *suffix;
    std::vector<Node *> labeled;

    Node(){
        start = end = len = -1;
        suffix = nullptr;
        labeled.assign(26, nullptr);
    }
};

class EerTree{
private:
    Node *root1;
    Node *root2;
    Node *current;

public:
    EerTree(){
        root1 = new Node();
        root1->len = -1;
        root1->suffix = root1;

        root2 = new Node();
        root2->len = 0;
        root2->suffix = root1;
        current = root2;
    }

    int insert(std::string &s, int pos){
        Node *cur = current;
        int letter = s[pos] - 'a';

        while(true){
            // loop is guranteed to break at root1
            if (pos - 1 - cur->len >= 0 && s[pos - 1 - cur->len] == s[pos])     
                break;
            cur = cur->suffix;
        }
        
        Node *temp = new Node();
        temp->len = cur->len + 2;
        temp->end = pos;
        temp->start = pos - temp->len + 1;
        cur->labeled[letter] = temp;

        if (temp->len == 1){
            // if cur is root1
            temp->suffix = root2;
            current = temp;
            return 0;
        }

        // find the suffix node

        while (true) {
            cur = cur->suffix;
            if((pos - 1 - cur->len) >= 0 && s[pos - 1 - cur->len] == s[pos]) {
                temp->suffix = cur->labeled[letter];
                break;
            }       
        }
        current = temp;

        return 0;
    }

    void print(std::string &s, Node *node){
        if(node != root1 || node != root2){
            for(int i = node->start; i <= node->end; ++i)
                std::cout << s[i];
            std::cout << '\n';
        }
        for(int i = 0; i < 26; ++i){
            if(node->labeled[i] != nullptr){
                print(s, node->labeled[i]);
            }
        }
    }

    void printAll(std::string &s){
        print(s, root1);
        print(s, root2);
    }

};

int main() {
    std::string s = "aabcba";
    EerTree tree;
    for(int i = 0; i < s.size(); ++i)
        tree.insert(s, i);
    std::cout << "insertion done\n";
    tree.printAll(s);
}

Applications

• Palindromic tree is used to store all palindromic substrings in a string.
• Palindromic tree can be used to count new palindromic subtrees after insertion in efficiently.
• It can be used to solve factorization problem in O(kn) time (arxiv 1506.04862 chapter 4).

References/ Further reading

• Original paper on Eertree : arxiv 1506.04862.
• Codeforce blogpost by adamant.