
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we are going to learn about the implementation of quick sort algorithm in Java.
Table of Contents:
- Working of Quick Sort
- Algorithm
- Jave Code using Naive partition
- Java Code using Hoare's partition
- Java Code using Lomuto's partition
- Detailed explanation of the implementation
- Arrays.sort in Java
- FAQs
Working of Quick Sort
Quick sort is a sorting algorithm based upon the divide and conquer approach. Let's take a brief look at the working of the quick sort algorithm.
1. Selection of the pivot element
The foremost thing is the selection of the pivot element of the array. Now this can be done in two ways:
Naive partition: In this case any element can be chosen as the pivot but takes O(n) extra space.
Hoare's partition: In this case the first element is selected as the pivot. The pivot element is not kept at the fixed position, it just partitions the array.
Lomuto's partition: In this case the last element is selected as the pivot. Traversal is done only once with a constance space complexity.
2. Rearranging the array
The array is rearranged in manner such that the elements smaller than the pivot are put on the left and once greater are put on the right of the pivot.
3. Divide Sub arrays
After the rearrangement of the array, pivot elements are chosen again and step 2 is repeated until the array is completely sorted.
Algorithm
Step 1: START
Step 2: Choose the pivot based on the type of partition you want, index based for naive partition, first element for Hoare's partition and last element for Lomuto's partition.
Step 3: Now take two variables indicating left and right of the array excluding the pivot.
Step 3: Keep moving towards right till the element on left is less than the pivot.
Step 4: Keep moving towards left till the element on right is greater than the pivot.
Step 5: If step 4 and 5 do not match then simply swap the left and right.
Step 6: if left become more than or equal to right then the point of their meeting becomes the new pivot.
Step 7: STOP
So for the implementation part, we are going to create a Java class with member methods like int partition(), void quick_sort() and void main(). Let's explore the int partition() method, its return type is int because it will return the position of the pivot element after each execution. Now the void quick_sort actually executes the quick sort alogrithm on both halves of the array based on the pivot returned by the pivot returned by the partition method. In the main method, we just create an array and call the methods to sort the array in the ascending order.
Java Code using Naive partition
public class Opengenus_QuickSort_NaivePartition {
public int partition(int[] arr, int low, int high) {
int temp[] = new int[(high - low) + 1];
int pivot = arr[high];
int index = 0;
// smaller number
for (int i = low; i <= high; ++i) {
if (arr[i] < pivot) {
temp[index++] = arr[i];
}
}
int pos = index;
temp[index++] = pivot;
for (int i = low; i <= high; ++i) {
if (arr[i] > pivot) {
temp[index++] = arr[i];
}
}
for (int i = low; i <= high; ++i) {
arr[i] = temp[i - low];
}
return pos;
}
public void quick_sort(int[] arr, int l, int h){
if(l < h){
int pivot = partition(arr, l, h);
quick_sort(arr, l, pivot - 1);
quick_sort(arr, pivot+1, h);
}
}
public static void main(String[] args){
int[] arr = {0, 5, 16, 10, 9, 8, 12};
Opengenus_QuickSort_NaivePartition obj = new Opengenus_QuickSort_NaivePartition();
obj.quick_sort(arr, 0, 6);
System.out.print("Sorted Array: ");
for(int i = 0 ; i < arr.length ; i++)
System.out.print(arr[i] + " ");
}
}
Output
Sorted Array: 0 5 8 9 10 12 16
Just like the Naive implementation, here we have int partition_Hoare and void quick_sort() methods that return the pivot index and perform quick sort respectively. The only difference is that here we have chosen first element as the pivot element.
Java Code using Hoare's partition
public class Opengenus_QuickSort_HoarePartition {
public int partition_Hoare(int[] arr, int low, int high) {
int pivot = arr[low];
int i = low - 1, j = high + 1;
while (true) {
do {
i++;
} while (arr[i] < pivot);
do {
j--;
} while (arr[j] > pivot);
if (i >= j)
return j;
// swapping the two values
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
public void quick_sort(int[] arr, int l, int h){
if(l < h){
int pivot = partition_Hoare(arr, l, h);
quick_sort(arr, l, pivot);
quick_sort(arr, pivot+1, h);
}
}
public static void main(String[] args){
int[] arr = {0, -5, 16, 10, 9, 8, 12};
Opengenus_QuickSort_HoarePartition obj = new Opengenus_QuickSort_HoarePartition();
obj.quick_sort(arr, 0, 6);
System.out.print("Sorted Array: ");
for(int i = 0 ; i < arr.length ; i++)
System.out.print(arr[i] + " ");
}
}
Output
Sorted Array: -5 0 8 9 10 12 16
Just like the Naive implementation, here we have int partition_Lomuto and void quick_sort() methods that return the pivot index and perform quick sort respectively. The only difference is that here we have last first element as the pivot element.
Java Code using Lomuto's partition
public class Opengenus_QuickSort_LomutoPartition {
public int lomuto_partition(int[] arr, int low, int high){
int pivot = arr[high];
int i = low - 1;
for(int j = low; j <= high - 1; j++){
if(arr[j] < pivot){
i++;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
int temp = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp;
return i+1; // returning index of the pivot element
}
public void quick_sort(int[] arr, int l, int h){
if(l < h){
int pivot = lomuto_partition(arr, l, h);
quick_sort(arr, l, pivot - 1);
quick_sort(arr, pivot+1, h);
}
}
public static void main(String[] args){
int[] arr = {0, 5, 16, 10, 9, 8, 12};
Opengenus_QuickSort_LomutoPartition obj = new Opengenus_QuickSort_LomutoPartition();
obj.quick_sort(arr, 0, 6);
System.out.print("Sorted Array: ");
for(int i = 0 ; i < arr.length ; i++)
System.out.print(arr[i] + " ");
}
}
Output
Sorted Array: 0 5 8 9 10 12 16
Detailed explanation of the implementation
Let us take a in-depth look at the implementation using an example, suppose we have an array of elements as 8, 4, 7, 9, 3, 10, 5, sorting the array using Lomuto's partion.
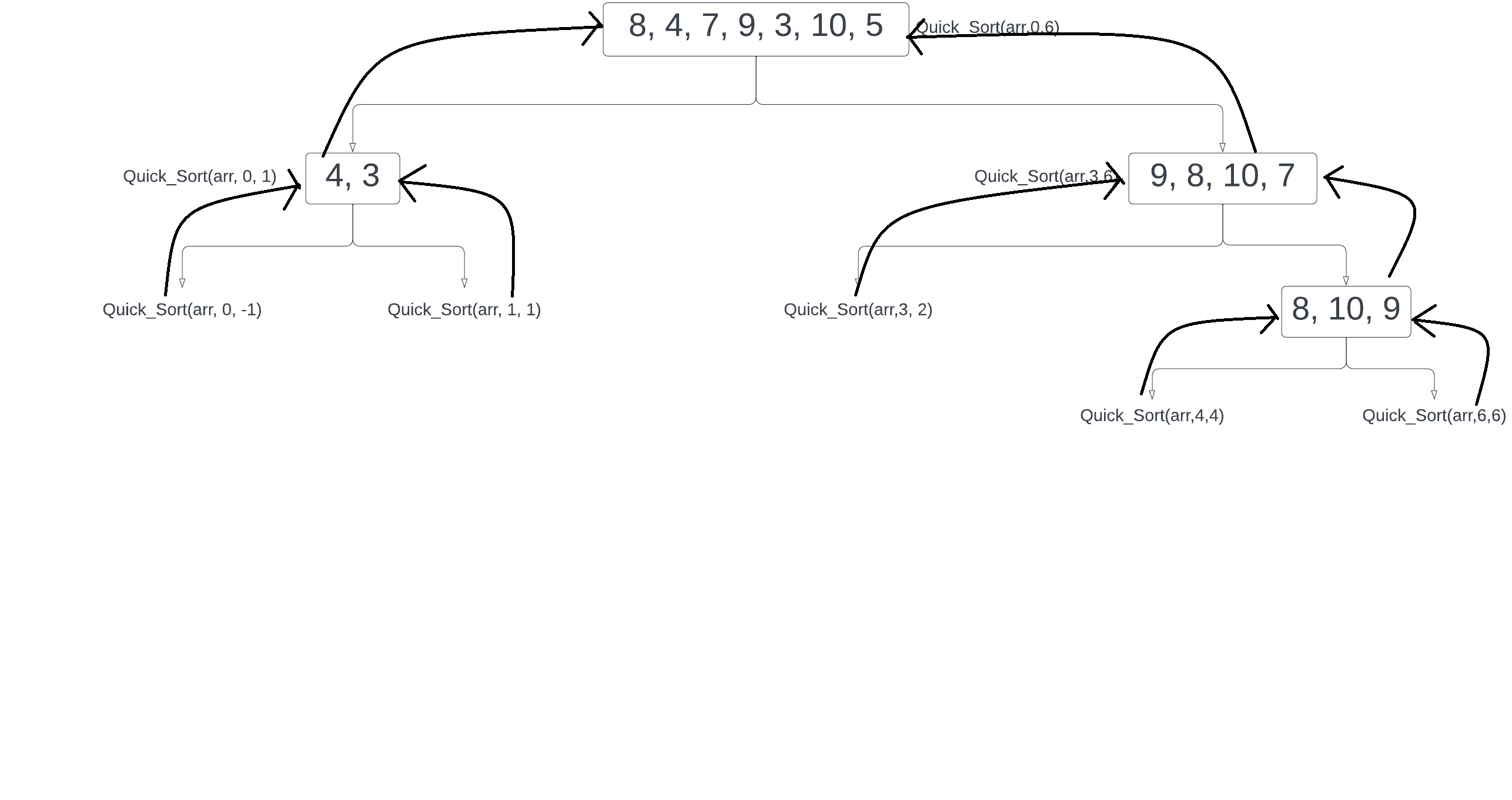
The above show quick sort working can be related to a Binary tree where the index of pivot element is the root and Quick_Sort(arr,l,p-1) reperesents the left sub-tree and Quick_Sort(arr,p+1,h) represents the right sub-tree.
We see that after every recursion call in the above given tree, the value is returned from the stack and then the array is finally sorted in the non-decreasing order.
Arrays.sort in Java
Array is a in-build java class that is used for performing searching, sorting, comparing and insertion operations on array. It is present in the java.utils package. sort() is one of the methods of the Arrays class that is used for sorting the array in non-decreasing order. It uses the quick sort algorithm for sorting the array elements. Here is the implementation:
import java.util.Arrays;
public class Opengenus_Arrays_Demo {
public static void main(String[] args){
int[] arr = {8, 4, 7, 9, 3, 10, 5};
Arrays.sort(arr);
System.out.println("Sorted Array: ");
for(int i = 0 ; i < 7 ; i++){
System.out.print(arr[i] + " ");
}
}
}
Output:
Sorted Array:
3 4 5 7 8 9 10
FAQs related to Quick Sort
1. Which is the fastest sorting algorithm?
Ans: Quick Sort is the fastest sorting algorithm.
2. What is the worst time complexity of quick sort algorithm?
Ans: The worst time complexity of quick sort is found to be O(n^2).
3. What is the approach on which the quick sort algorithm is based?
Ans: Quick sort algorithm is based upon the divide and conquer approach.
4. What is the best method to choose partition in quick sort?
Ans: Random picking is the best choice for partition in quick sort.
5. What is the average running time of quick sort algorithm?
Ans: The average running time of quick sort algorithm is O(n Logn).
Thank You!
