Regular Expression in Theory of Computation

Regular expressions are used to describe languages, in this article we discuss regular expressions and show that every language can be described by a regular expression.

Table of contents.

1. Introduction.
2. Regular Expressions.
3. Equivalence of regular expressions and regular languages.
4. Summary.
5. References.

Prerequisites.

1. regular operations.

Introduction.

Regular expressions are a means to describe languages, they define a finite pattern of strings or symbols.
Each pattern will match a set of strings and therefore they serve as names for a set of strings.

Regular Expressions.

To get a idea about what regular expressions involve, let's go through a few examples:

Example 1:
Consider the expression (0 ∪ 1)01*.
The language that is described by the above expression is the set of all binary strings,

• that start with 0 or 1 as indicated by 0 ∪ 1,
• for which the second symbol is 0,
• that end with zero or more 1s as indicated by 1*.

A sample language is such as the following;
{00, 001, 0011, 00111, ..., 10, 101, 1011, 10111, ...}

Example 2:
The expression 1*01*01* defines the language:
{w : w contains exactly two 0s}

Example 3: The expression 1011 ∪ 0 describes the language {1011, 0}.

Example 4: The expression ((0 ∪ 1)(0 ∪ 1))* describes the language {w : the length of w is even}

Example 5: The expression (0 ∪ 1)*1011(0 ∪ 1)* describes the language {w : 1011 is a substring of w}

Example 6: The expression (0 ∪ 1)*0(0 ∪ 1)*0(0 ∪ 1)* describes the language {w : w contains at least two 0s}

Definition 1: Let Σ be a non-empty alphabet.

1. ϵ is a regular expression.
2. ∅ is a regular expression.
3. For each a ∈ Σ, a is a regular expression.
4. If R1 and R2 are regular expressions, then R1 ∪ R2 is also a regular expression.
5. If R1 and R2 are regular expressions, then R1R2 is also a regular expression.
6. If R, then R* is also a regular expression.

From the above listing, 1-3 are regarded as the building blocks of regular expressions while 3-6 define rules used to combine regular expressions into new/larger regular expressions.

An example: We claim that (0 ∪ 1)*101(0 ∪ 1)* is a regular expression where the alphabet Σ is {0, 1}.
Proof: We have to show that the expression can be built using the rules defined above.

• By rule 3, 0 and 1 are regular expressions.
• By rule 4, 0 ∪ 1 is a regular expression since both 0 and 1 are regular expressions.
• By rule 5, 10 and 101 are both regular expressions.
• By rule 5, (0 ∪ 1)*101 is a regular expression since (0∪1)* and 101 are also regular expressions.
• By rule 5, (0 ∪ 1)*101(0 ∪ 1)* is a regular expression since (0∪1)*101 and (0∪1)* are both regular expressions.
• By rule 6, (0 ∪ 1)* is a regular expression.

Now we define the language that is described by the above regular expressions.

1. ϵ describes the language {ϵ}.
2. ∅ describes the language {∅}.
3. For each a ∈ Σ, a describes the language {a}.
4. Let R1 and R2 be regular expressions and L1 and L2 be the languages described by these expressions respectively. The regular expressions R1 ∪ R2 describes the language L1 ∪ L2.
5. Also assume the above for the languages L1 and L2 and the expressions R1 and R2, The regular expression R1R2 also describes the language L1L2.
6. Let R be a regular expression and L be the language described by it. The regular expression R* describes the language L*.

Example 1:
Regular expression 0 ∪ ϵ describes the language {0, ϵ} whereas the expression 1* describes the language {ϵ, 1, 11, 111, ..., } and therefore, the regular expression (0 ∪ ϵ)1* describes the language {0, 01, 011, 0111, ..., ϵ, 1, 11, 111, ...}.

Example 2: Regular expression (0 ∪ ϵ)(1 ∪ ϵ) describes the language {01, 0, 1, ϵ}.

Definition 2: Let R1 and R2 be regular expressions and L1 and L2 be languages described by the expressions, then if L1 = L2, that is, R1 and R1 describe the same language, then we can write R1 = R2.
Therefore, even if (0 ∪ ϵ)1* and 01* ∪ 1* are different regular expressions, we can write,
(0 ∪ ϵ)1* = 01* ∪ 1*
because they describe the same language.

Theorem: Let R1, R2, R3 be regular expressions. The following identities hold.

1. R1∅ = ∅R1 = ∅.
2. R1ϵ = ϵR1 = R1.
3. R1 ∪ ∅ = ∅ ∪ R1 = R1.
4. R1 ∪ R1 = R1.
5. R1 ∪ R2 = R2 ∪ R1.
6. R1(R2 ∪ R3) = R1R2 ∪ R1R3.
7. (R1 ∪ R2)R3 = R1R3 ∪ R2R3.
8. R1(R2R3) = (R1R2)R3.
9. ∅* = ϵ.
10. ϵ* = ϵ.
11. (ϵ ∪ R1)* = R1*.
12. (ϵ ∪ R1)(ϵ ∪ R1)* = R1*.
13. R1*(ϵ ∪ R1) = (ϵ ∪ R1)R1*=R1*.
14. R1*R2 ∪ R2 = R1*R2.
15. R1(R2R1)* = (R1R2)*R1.
16. (R1 ∪ R2)*= (R1*R2)*R1* = (R2*R1)*R2*.

We shall not present proof for the above identities however we assume they are verified.
For example: We can verify the identity (0 ∪ ϵ)1* = 01* ∪ 1* as follows,

• By identity 7: (0 ∪ ϵ)1* = 01* ∪ ϵ1*
• By identity 2: (0 ∪ ϵ)1* = 01* ∪ 1*

Equivalence of regular expressions and regular languages.

Theorem: Let L be a language, then L is regular iff there exists a regular expression describing L.

The proof of this theorem entails two parts:

1. First we will prove that every regular expression describes a regular language.
2. Second, we prove that every DFA M can be converted to a regular expression describing a language L(M).

1. Every regular expression describes a regular language

Let R be an arbitrary regular expression over the alphabet Σ.
We need to prove that the language that is described by R is a regular language.
We prove using induction on the structure of R, that is, by induction on the way R is built using the rules we defined earlier(definition 1).

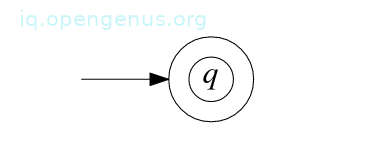
Base case 1: Assuming R = ϵ, then R describes the language {ϵ} and to prove that it is regular we shall construct a NFA M = (Q,Σ, δ, q, F) that accepts this language.

We obtain this NFA by defining
Q = {q}, q the start state, F = {q} and δ(q, a) = ∅ for all a ∈ Σϵ
State diagram of M:

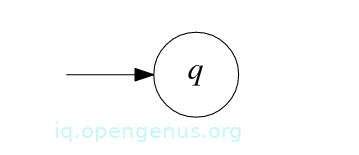
Base case 2: Assuming R = ∅, then R describes the language ∅ and to prove that it is regular, we construct an NFA M = (Q,Σ, δ, q, F) that accepts it. We obtain this NFA by defining Q = {q}, q the start state, F = ∅, and δ(q, a) = ∅ for all a ∈ Σϵ.
The state diagram of M:

Base case 3: Let a ∈ Σ, assume R = a, then R describes the language {a} and to prove that it is regular we construct a NFA M= (Q,Σ, δ, q1, F) that accepts it. The NFA is obtained by defining Q = {q1, q2}, q1 is the start state, F = {q2}, and
δ(q1, a) = {q2},
δ(q1, b) = ∅ for all b ∈ Σϵ \ {a},
δ(q2, b) = ∅ for all b ∈ Σϵ.
State diagram of M is shown below.

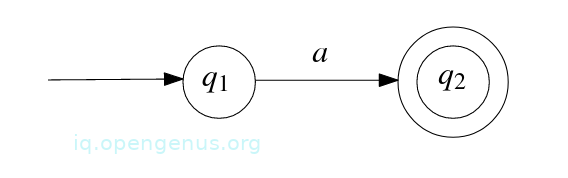
Induction step 1 of base case 1: Assuming R = R1 ∪ R2 where R1 and R2 are regular expressions. Let L1 and L2 be regular languages described by R1 and R2 respectively, then R describes the language L1 ∪ L2 which is also regular by Theorem 1.1 in the prerequisite article.

Induction step of base case 2: Assuming that R = R1R2 where R1 and R2 are regular expressions. Let L1 and L2 be two regular languages described by the regular expressions respectively, then R describes the language L1L2 which by Theorem 4 in the prerequisite article is regular.

Induction step of base case 3: Assuming that R = (R1)* where R1 is regular expression. Let L1 be the language described by R1 and assuming that L1 is regular, then R describes the language (L1)* which by Theorem 5 in the prerequisite article is regular.

At this point we conclude the proof of the claim that every regular expression describes a regular language.

An example:
Consider the regular expression: (ab ∪ a)*, where {a, b} is the alphabet. We construct a NFA that accepts the language described by the regular expression to prove that the regular expression describes a regular language.
Lets first build a regular expression:

• First we take the regular expressions a and b and combine them to a regular expression ab.
• Next, we take the regular expressions ab and a and combine them into regular expression ab ∪ a.
• We take regular expression ab ∪ a and transform it into the regular expression (ab ∪ a)*.

Now to construct an NFA:

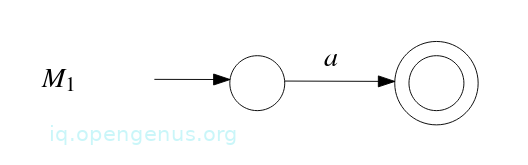
• We construct NFA M1 that accepts the language described by regular expression a:

• We construct NFA M2 that accepts the language described by regular expression b:

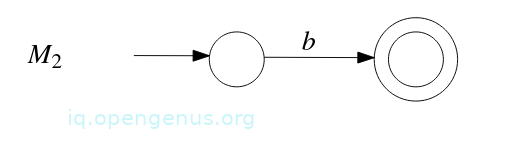
• Apply the construction from the proof of Theorem 4(prerequisite article) to M1 and M2 which gives NFA M3 that accepts the language described by the regular expression ab:

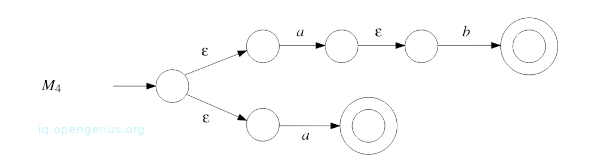
• Apply the construction from proof of Theorem 1.1:(prerequisite article) to M1 and M3 which gives NFA M4 that accepts the language described by regular expression ab ∪ a:

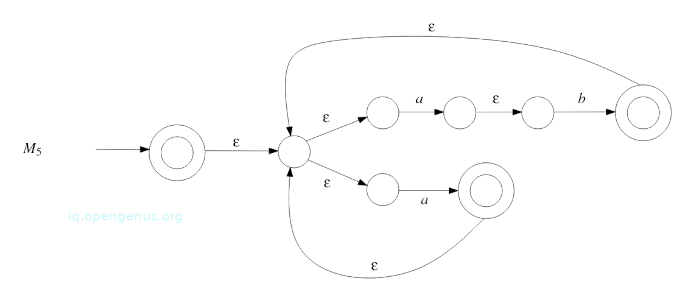
• Apply construction from proof of Theorem 5(prerequisite article) to M4 which gives NFA M5 that accepts language described by regular expression (ab ∪ a)*

2. Converting a DFA to a regular expression.

We will prove that every DFA M can be converted into a regular expression describing a language L(M).
First we solve recurrence relations involving languages.

Solving recurrence relations.
Let Σ be an alphabet, B and C be known languages in Σ* such that ϵ ∉ B and L be an unknown language such that L = BL ∪ C.
Let's try to express L in terms of B and C hence solving it.

To start consider an arbitrary string u in language L. Now to determine how u looks like. Since u ∈ L and L = BL ∪ C, we know u is a string in BL ∪ C and therefore we have the following possibilities:

1. u is an element of C.
2. u is an element of BL, if this is the case, then there are strings b ∈ B and v ∈ L such that u = bv. Since ϵ ∉ B, we have b ≠ ϵ and thus, |v| < |u|. Since v is a string in L which is equal to BL ∪ C, v is a string in BL ∪ C and we have the following possibilities for v.

• v is an element of C, if this is the case, u = bv where b ∈ B and v ∈ C and therefore u ∈ BC.
• v is an element of BL, if this is the case, there are strings b′ ∈ B and w ∈ L such that v = b′ w. Since ϵ ∉ B we have b′ ≠ ϵ, therefore, |w| < |v|. Since w is a string in L, there are two further possibilities.
  ** w is an element of C, if this is the case, u = bb′ w, where b, bb′ ∈ B and w ∈ C, therefore u ∈ BBC.
  ** w is an element of BL, if this is the case, there are strings b′′ ∈ B and x ∈ L such that w = b′′x. Since ≠ ϵ B we have b′′ ≠ ϵ and therefore *|x| < |w|. Since x is a string in L, x is also a string in BL ∪ C and we have another two further possibilities for x.
  *** x is an element in C, if this is the case, u = bb′ b′′ x where b, b′, b′′ ∈ B and x ∈ C and therefore u ∈ BBBC.
  *** x is an element of BL and so on...

From the above we are convinced that any string u in L can be written as a concatenation of zero or more strings in B followed by one string in C.

Lemma 1: Let Σ be an alphabet and B, C, L, be languages in Σ* such that ϵ ≠ B and L = BL ∪ C, then L = B*C.

Proof:
We first show that B*C ⊆ L. Let u be an arbitrary string B*C. Then u is the concatenation of k strings of B for some k ≥ 0 followed by one string of C.

The base case: k = 0, u is a string in C, therefore u is a string in BL ∪ C. Since L = BL ∪ C, u is a string in L.

Inductive step: k ≥ 1, we write u = vwc where v is a string in B, w is the concatenation of k-1 strings of B and c is a string of C.
We define y = wc and observe that y is the concatenation of k-1 strings of B followed by a single string of C.
By induction, string y is an element of L, therefore u = vy where v is a string in B and y a string in L.
This shows that u is a string in BL and therefore u is a string in BL ∪ C and since L = BL ∪ C if follows that u is a string in L.
We have completed the proof that B*C ⊆ L.

To show that L ⊆ B*C, let u be an arbitrary string in L and l its length. By induction we will prove that u is a string in B*C.

Base case: l = 0, u = ϵ and since u ∈ L and L = BL ∪ C, u is a string in BL ∪ C. Since ϵ ≠ B, u cannot be a string in BL and hence u must be a string in C.
Since C ⊆ B*C, u is a string in B*C.

Induction step: l ≥ 1, If u is a string in C, u is a string in B*C and we are done.

Assuming u is not a string in C. Since u ∈ L and L = BL ∪ C, u is a string in BL. Therefore there are strings b ∈ B and v ∈ L such that u = bv.
Since ϵ ≠ B, the length of b is greater or equal to 1 and therefore the length of v is less than the length of u.
By induction, v is a string in B*C and hence u = bv where b ∈ B and v ∈ B*C which shows u ∈ B(B*C). Since B(B*C) ⊆ B*C, it shows that u ∈ B*C.

This lemma holds for any language B that doesn't contains an empty string ϵ.

Converting DFA to regular expression.
We use lemma 1 to prove that every DFA can be converted to a regular expression.
Let M = (Q,Σ, δ, q, F) be an arbitrary deterministic finite automaton.
We will show that there exists a regular expression that describes a language L(M).

For each state r ∈ Q we define:
Lr={w ∈ Σ*: the path in the state diagram of M that starts in state r and corresponds to w ends in state F}. That is, Lr is the language accepted by M , if r was the start state.
Now we show that Lr can be described by a regular expression, Since L(M) = Lq, it proves that L(M) can be described by a regular expression.

The idea is to set up equations for the languages Lr which we then solve using lemma 1.
We claim that
${\mathrm{L}}_{\mathrm{r}}=\bigcup _{\mathrm{a}\in \mathrm{\Sigma }}^{}\mathrm{a}.{\mathrm{L}}_{\mathrm{\delta }(\mathrm{r},\mathrm{a}) } \mathrm{if} \mathrm{r}\notin \mathrm{F}$

Let w be a string Lr, then the path P in the state diagram of M starting in state r and corresponding to w ends in state F.
Since r ∉ F, this path contains at least one edge.
Let r′ be the following state after the first state, then r′ = δ(r, b) for some symbol b ∈ Σ.
Therefore, b is the first symbol of w.
We write w = bv where v is the remaining part of w.
Then the path P′ = P \ {r} in the state diagram M starting in state r′ and corresponding to v ends in state F.
Thus, v ∈ Lr′ = Lδ(r, b).
Hence:
$\mathrm{w}\in \mathrm{b}.{\mathrm{L}}_{\mathrm{\delta }\left(\mathrm{r},\mathrm{b}\right) }\subseteq \bigcup _{\mathrm{a}\in \mathrm{\Sigma }}^{}\mathrm{a}.{\mathrm{L}}_{\mathrm{\delta }\left(\mathrm{r},\mathrm{a}\right) }$

Conversely, let w be a string in ${\bigcup }_{\mathrm{a}\in \mathrm{\Sigma }}^{}\mathrm{a}.{\mathrm{L}}_{\mathrm{\delta }\left(\mathrm{r},\mathrm{a}\right) }$, then there is a symbol b ∈ Σ and a string v ∈ ${\mathrm{L}}_{\mathrm{\delta }\left(\mathrm{r},\mathrm{b}\right) }$ such that w = bv.
Let P′ be a path in the state diagram of M starting in state δ(r, b) and corresponding to v.
Since v ∈ ${\mathrm{L}}_{\mathrm{\delta }\left(\mathrm{r},\mathrm{b}\right) }$, this path ends in a state F.
Let P be the path in the state diagram of M starting in r and follows the edge to δ(r, b), then follows P′.
This path corresponds to w and end in a state F and therefore w ∈ Lr.
We complete the proof of the claim.

In a similar fashion we can prove that:
${\mathrm{L}}_{\mathrm{r}}=ϵ\cup (\bigcup _{\mathrm{a}\in \mathrm{\Sigma }}^{}\mathrm{a}.{\mathrm{L}}_{\mathrm{\delta }(\mathrm{r},\mathrm{a}) }) \mathrm{if} \mathrm{r}\notin \mathrm{F}$

In this case we have a set of equations in the unknowns Lr for r ∈ Q.
The total number of equations is equal to the number of unknowns(size of Q).
To obtain the regular expression of L(M) = Lq) we solve the equations using lemma 1, for this we have to convince ourselves that these equations have a solution for any DFA.

Lemma 2: Let n ≥ 1 be an integer and for 1 ≤ i ≤ n and 1 ≤ j ≤ n, let ${\mathrm{B}}_{\mathrm{ij}}$ and ${\mathrm{C}}_{\mathrm{i}}$ be regular expressions such that ϵ ≠ ${\mathrm{B}}_{\mathrm{ij}}$. Let L1, L2, ..., Ln be languages satisfying:
${\mathrm{L}}_{\mathrm{i}}=\left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{B}}_{\mathrm{ij}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{C}}_{\mathrm{i}} \mathrm{for} 1\le \mathrm{i}\le \mathrm{n}$

Then L1 is expressed as a regular expression by involving regular expressions ${\mathrm{B}}_{\mathrm{ij}}$ and ${\mathrm{C}}_{\mathrm{i}}$.

Proof: We prove this lemma by an induction on n.
Base case: n = 1, therefore, we have
L1 = ${\mathrm{B}}_{\mathrm{11}}$ ${\mathrm{L}}_1$ ∪ ${\mathrm{C}}_1$

Since ϵ ∉ ${\mathrm{B}}_{\mathrm{11}}$, by lemma 1 that L1 = ${{\mathrm{B}}^{*}}_{11}$${\mathrm{C}}_{\mathrm{1}}$, this proves the base case.

Induction step: Let n ≥ 2, we assume that the lemma is true for n-1, we have:
${\mathrm{L}}_{\mathrm{n}}=\left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{B}}_{\mathrm{nj}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{C}}_{\mathrm{n}}$

= ${\mathrm{B}}_{\mathrm{nn}}{\mathrm{L}}_{\mathrm{n}}\cup \left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}-1}{\mathrm{B}}_{\mathrm{nj}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{C}}_{\mathrm{n}}$

Since ϵ ∉ ${\mathrm{B}}_{\mathrm{nn}}$, then from lemma 1:

${\mathrm{L}}_{\mathrm{n}}={\mathrm{B}}_{\mathrm{nn}}^{*}\left(\left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}-1}{\mathrm{B}}_{\mathrm{nj}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{C}}_{\mathrm{n}}\right)$

= ${\mathrm{B}}_{\mathrm{nn}}^{*}\left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}-1}{\mathrm{B}}_{\mathrm{nj}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{B}}_{\mathrm{nn}}^{*}{\mathrm{C}}_{\mathrm{n}}$

= $\left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}-1}{\mathrm{B}}_{\mathrm{nn}}^{*}{\mathrm{B}}_{\mathrm{nj}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{B}}_{\mathrm{nn}}^{*}{\mathrm{C}}_{\mathrm{n}}$

By substituting the equation for Ln, into equations for Li, 1 ≤ i ≤ n − 1 we obtain the equation.
${\mathrm{L}}_{\mathrm{i}}=\left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{B}}_{\mathrm{ij}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{C}}_{\mathrm{i}}$

= ${\mathrm{B}}_{\mathrm{in}}{\mathrm{L}}_{\mathrm{n}}\cup \left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}-1}{\mathrm{B}}_{\mathrm{ij}}{\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{C}}_{\mathrm{i}}$

= $\left(\bigcup _{\mathrm{j}=1}^{\mathrm{n}-1}({\mathrm{B}}_{\mathrm{in}}{\mathrm{B}}_{\mathrm{nn}}^{*}{\mathrm{B}}_{\mathrm{nj}}\cup {\mathrm{B}}_{\mathrm{ij}}){\mathrm{L}}_{\mathrm{j}}\right)\cup {\mathrm{B}}_{\mathrm{in}}{\mathrm{B}}_{\mathrm{nn}}^{*}{\mathrm{C}}_{\mathrm{n}}\cup {\mathrm{C}}_{\mathrm{i}}$

An therefore we have n-1 equations in L1, L2,...,Ln-1 and since $\mathrm{ϵ}\notin {\mathrm{B}}_{\mathrm{in}}{\mathrm{B}}_{\mathrm{nn}}^{*}{\mathrm{B}}_{\mathrm{nj}}\cup {\mathrm{B}}_{\mathrm{ij}}$, it follows from the induction hypothesis that L1 can be expressed as a regular expression only involving the regular expressions ${\mathrm{B}}_{\mathrm{ij}}$ and ${\mathrm{C}}_{\mathrm{i}}$

Summary.

Regular expressions are a means to describe languages, in this article, we proved that every regular expression describes a regular language and that every DFA can be converted to a regular expression that describes a language.